数据结构–最短路径 Floyd算法

$Floyd算法：求出每⼀对顶点之间的最短路径$
使⽤动态规划思想，将问题的求解分为多个阶段
对于n个顶点的图G，求任意⼀对顶点 $V_i\to V_j$ 之间的最短路径可分为如下⼏个阶段：
#初始：不允许在其他顶点中转，最短路径是？
#0：若允许在 V0 中转，最短路径是？
#1：若允许在 V0、V1 中转，最短路径是？
#2：若允许在 V0、V1、V2 中转，最短路径是？
…
#n-1：若允许在 V0、V1、V2 …… Vn-1 中转，最短路径是？

Floyd算法是一种用于寻找图中任意两个节点之间最短路径的算法，它的步骤如下：

1. 创建一个二维数组dist，用于存储任意两个节点之间的最短路径长度。初始时，dist的值为图中两个节点之间的直接路径长度，如果两个节点之间没有直接路径，则设置为无穷大。
2. 创建一个二维数组path，用于存储任意两个节点之间的最短路径的中间节点。初始时，path的值为起始节点到终点节点的直接路径上的终点节点。
3. 使用三重循环，遍历所有节点，每次循环中选择一个节点k作为中间节点，更新dist和path数组的值。
   a. 对于每对节点i和j，如果通过节点k可以使得从节点i到节点j的路径更短，则更新dist[i][j]的值为dist[i][k] + dist[k][j]，并更新path[i][j]的值为节点k。
   b. 如果dist[i][j]的值变小了，说明找到了一条更短的路径，需要更新path[i][j]的值为节点k。
4. 重复步骤3，直到遍历完所有节点。
5. 根据path数组，可以构建任意两个节点之间的最短路径。

以上就是Floyd算法的基本步骤。

Floyd算法的时间复杂度为$O(n^3)$，其中n为节点的个数。

$\begin{array}{rlrl}& \text{若}& & {\mathrm{A}}^{(k-1)}[i][j]>{\mathrm{A}}^{(k-1)}[i][k]+{\mathrm{A}}^{(k-1)}[k][j]\\ & \text{则}& & \mathbf{A}(k)[i][j]={\mathbf{A}}^{(k-1)}[i][k]+{\mathbf{A}}^{(k-1)}[k][j];\\ & & & {\mathrm{path}}^{(k)}[i][j]=k\\ & \text{否则}& & A^{(k)}{\text{ 和 path}}^{(k)}\text{ 保持原值}\end{array}$

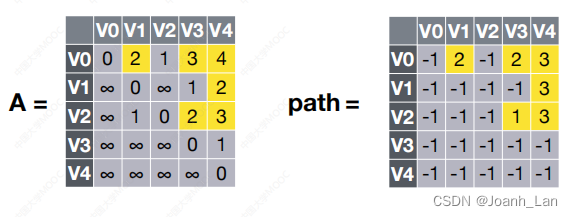
V0到V4 最短路径⻓度为 A[0][4]=4
通过path矩阵递归地找到完整路径：

注：
Floyd算法可以⽤于负权图
Floyd 算法不能解决带有“负权回路”的图（有负权值的边组成回路），这种图有可能没有最短路径

eg:

## 代码

void floyd()
{
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++){
dist[i][j] = map[i][j],
path[i][j] = 0; }
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(dist[i][k] + dist[k][j] < dist[i][j]){
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = k; //中转点}}

知识点回顾与重要考点

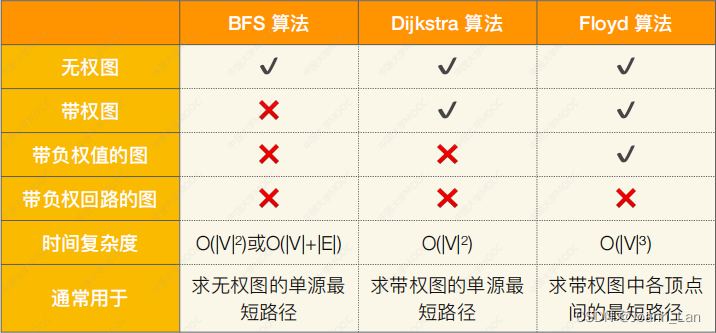
注：也可⽤ Dijkstra 算法求所有顶点间的最短路径，重复 |V| 次即可，总的时间复杂度也是$O(|V{|}^3)$