一、前言

字符串匹配

import re
print(re.search('www', 'www.runoob.com').span())  # 在起始位置匹配
print(re.search('com', 'www.runoob.com').span())  # 不在起始位置匹配

SQL中的匹配

SELECT * FROM Persons
WHERE City LIKE '%lon%'

我们注意到这些都是需要用到字符串匹配的，我们再深入想一下，这些字符串是怎么匹配的呢？

二、暴力解法

public class baoli {public static void main(String[] args) {String text = "ABABDABACDABABCABAB";//19String pattern = "ABABCABAB";//9int index = bruteForceMatch(text, pattern);if (index == -1) {System.out.println("Pattern not found in the text");} else {System.out.println("Pattern found at index " + index);}}public static int bruteForceMatch(String text, String pattern){int n = text.length();int m = pattern.length();for (int i = 0; i <= n - m; i++) {int j;for (j = 0; j < m; j++) {if (text.charAt(i + j) != pattern.charAt(j)) {break;}}if (j == m) {return i; // 匹配成功，返回起始位置}}return -1; // 匹配失败}
}

看到这种brute force暴力解法的时间复杂度为O(mn)

一个字一个字的匹配，一旦出错就匹配下一个

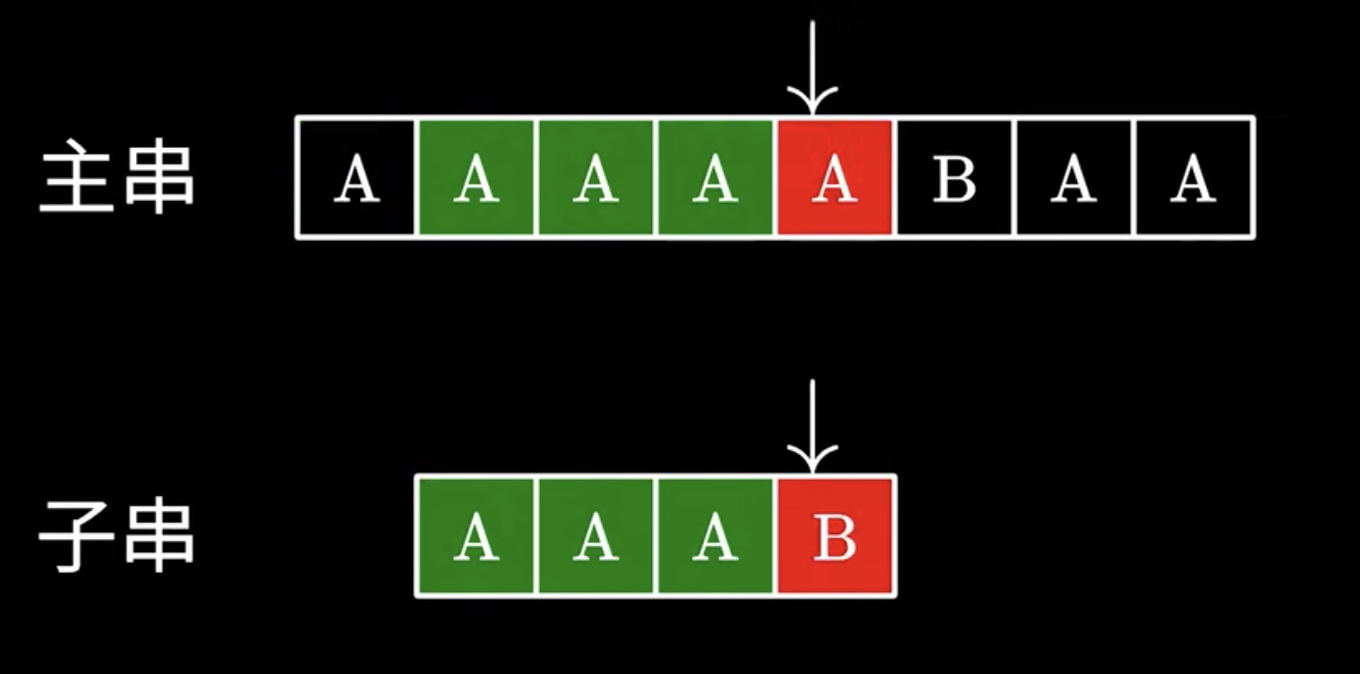
在这里插入图片描述
但是这样带来了巨大的浪费

三、KMP算法原理

在这里插入图片描述

KMP算法是用的这三位大佬的名字首字母，没有什么特殊含义

3.1 自动子串的指针

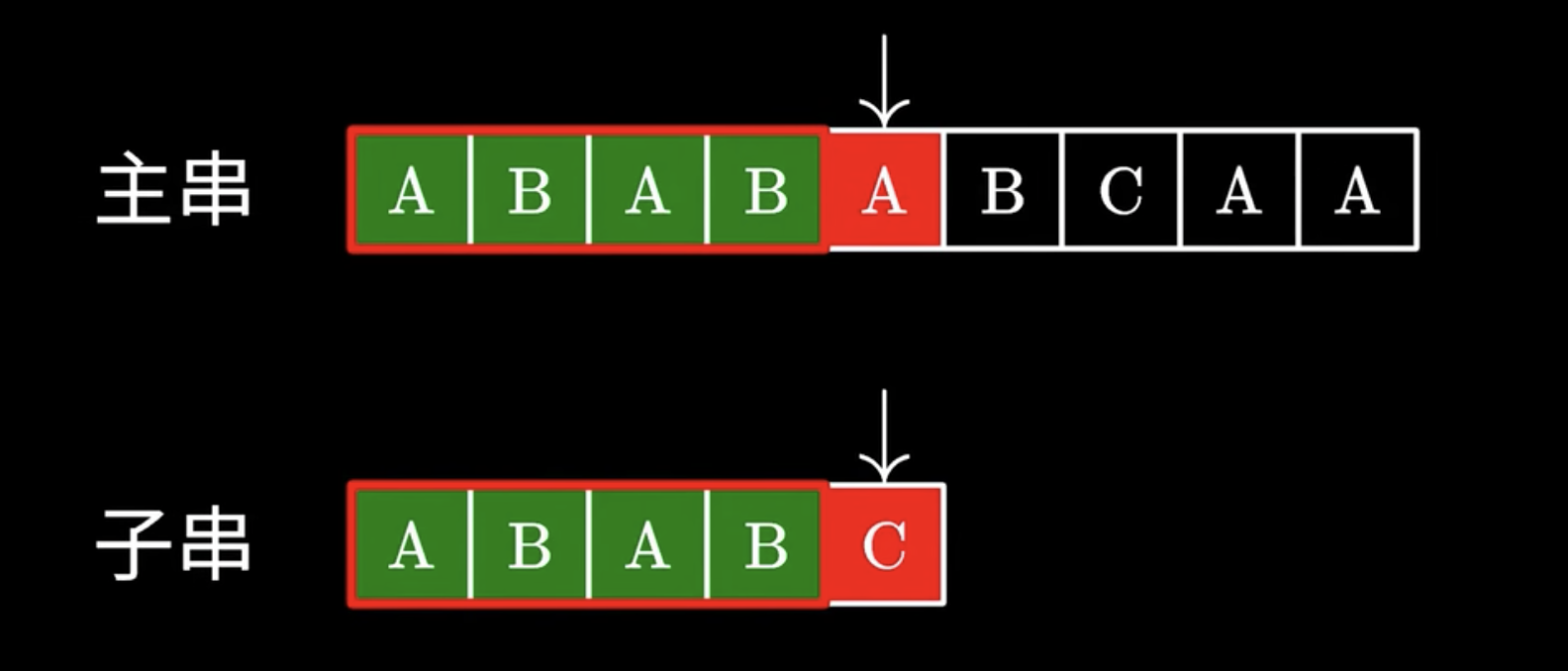
在这里插入图片描述
匹配失败，已经知道了前面读过了哪些char，所以移动子串的指针

在这里插入图片描述

3.2 跳过多少个字符

在这里插入图片描述

KMP算法会定义一个next数组，记录对应可以跳过字符的个数

    public static int kmpSearch(String text, String pattern) {int[] next = computeLPSArray(pattern);int i = 0; // text的指针int j = 0; // pattern的指针while (i < text.length()) {if (text.charAt(i) == pattern.charAt(j)) { // char匹配，都后移i++;j++;if (j == pattern.length()) {return i - j; // string匹配成功，返回起始位置}} else {if (j != 0) { // char匹配失败，pattern回退到上一个匹配的位置j = next[j - 1];} else { // 字符串第一个就匹配失败，直接后移i++;}}}return -1; // 匹配失败}

3.3 next数组 - 暴力

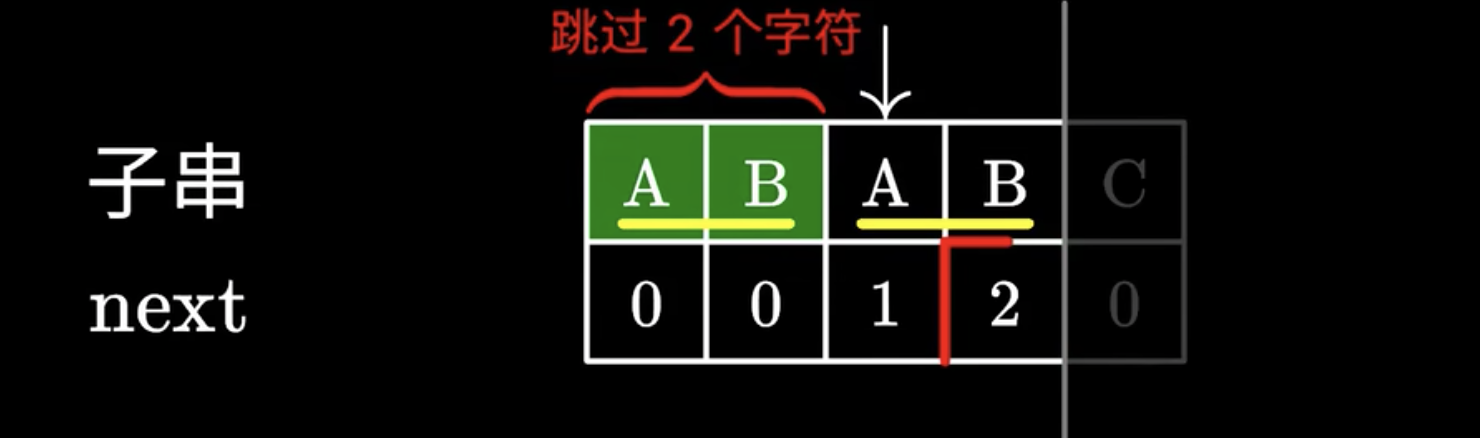
在这里插入图片描述

next数组：寻找子串中“相同前后缀的最长长度，不能是字符串本身”

那么如何获取这个next数组呢，当然首先可以想到for循环暴力求解

    public static int[] bruteComputeLPSArray(String pattern) {int[] lps = new int[pattern.length()];int len = 0;for (int i = 1; i <= pattern.length() - 1; i++) {if (pattern.charAt(i) == pattern.charAt(len)) {len++;lps[i] = len;} else {if (len != 0) {len = lps[len - 1];i--;} else {lps[i] = 0;}}}return lps;}

3.4 next数组 - 求解

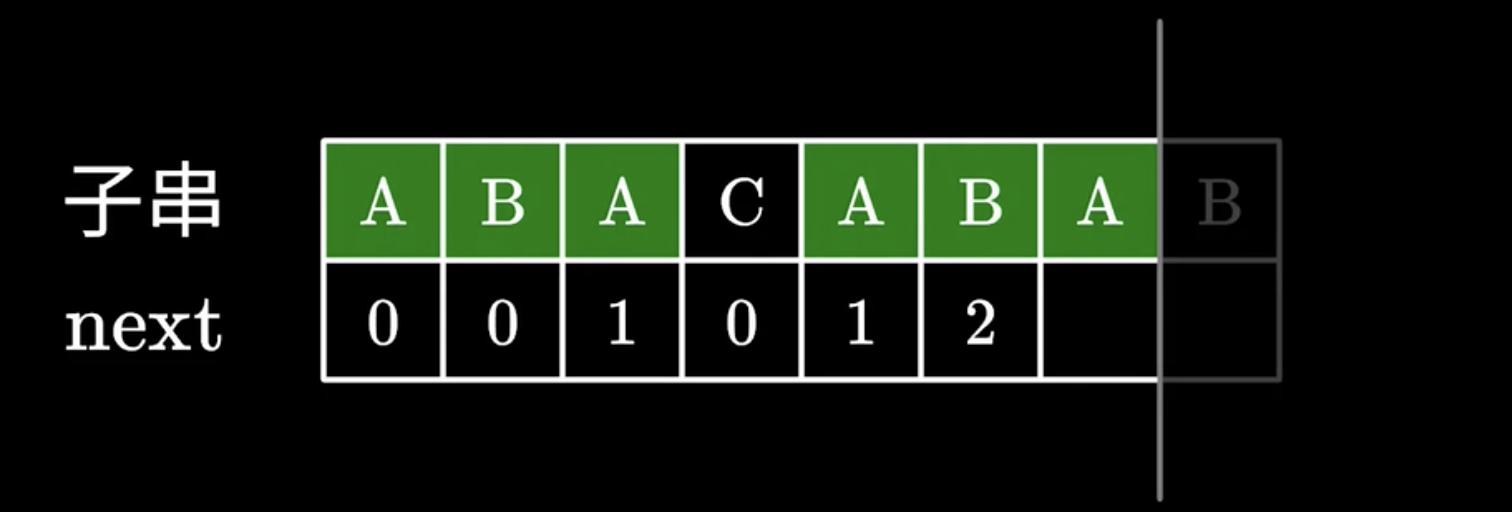
在这里插入图片描述

下一步相同，那么直接就是2+1
下一步不同呢？

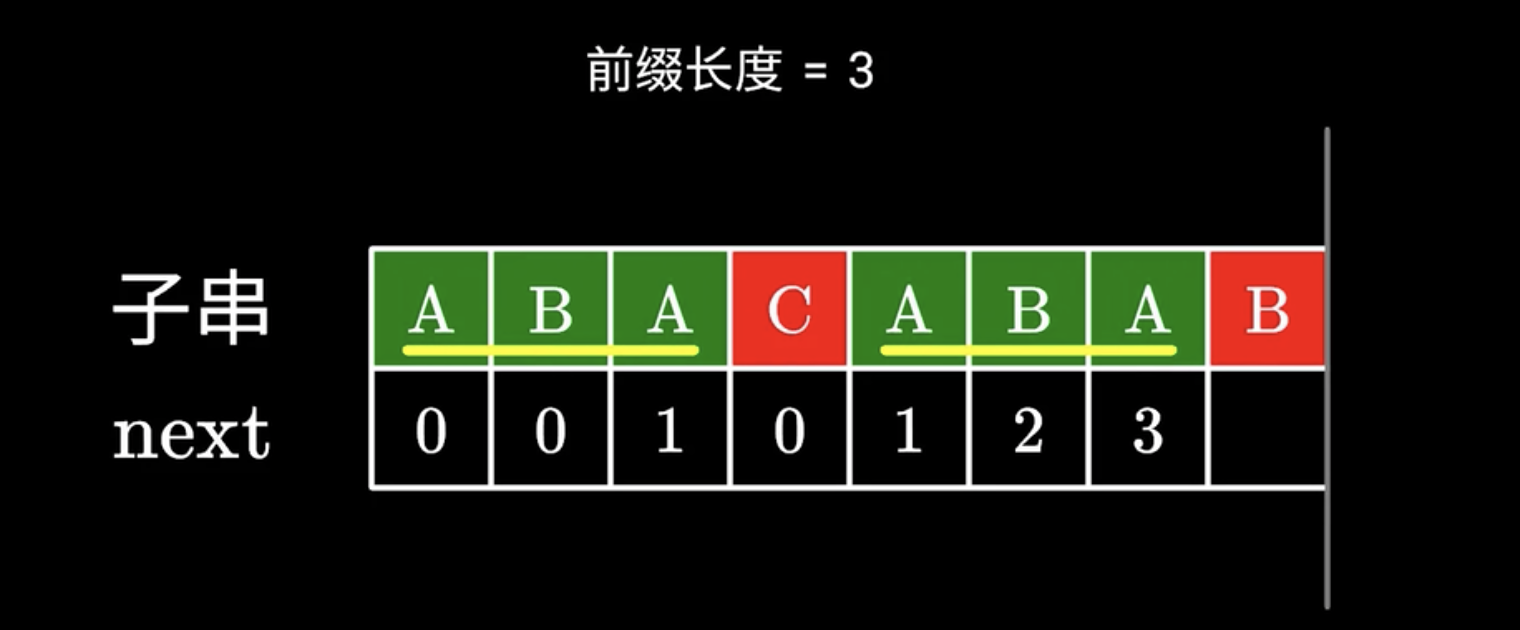
在这里插入图片描述

左边这部分前后缀 = 右边这部分前后缀

直接在左边进行查找即可

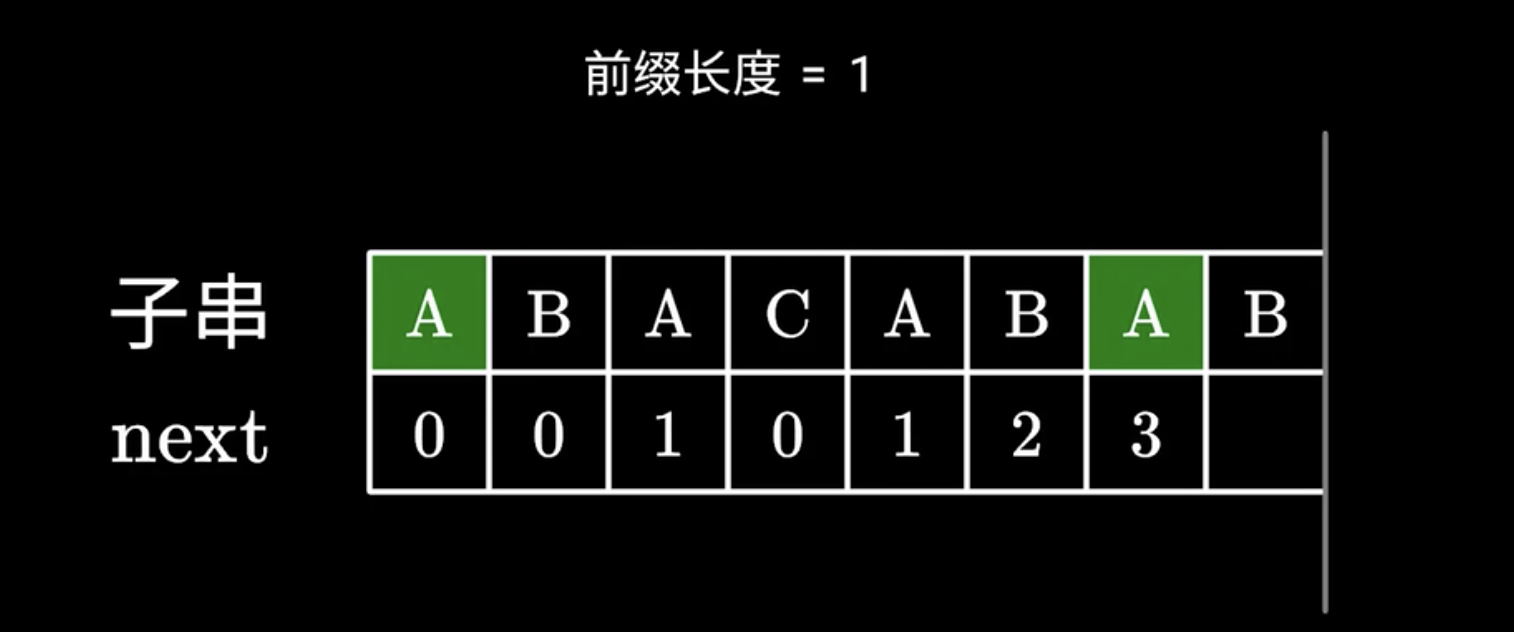
在这里插入图片描述
于是又开始，寻找下一个char是否相同

    public static int[] computeLPSArray(String pattern) {int[] next = new int[pattern.length()];int len = 0; // 最长公共前后缀的长度int i = 1; // pattern的指针while (i < pattern.length()) {if (pattern.charAt(i) == pattern.charAt(len)) {len++;next[i] = len;i++;} else {if (len != 0) {len = next[len - 1]; // 回退到前一个匹配的位置} else {next[i] = 0;i++;}}}return next;}

四 KMP实现

package com.KMP;public class KMPAlgorithm {public static void main(String[] args) {String text = "ABABDABACDABABCABAB";String pattern = "ABABCABAB";int index = kmpSearch(text, pattern);if (index == -1) {System.out.println("Pattern not found in the text");} else {System.out.println("Pattern found at index " + index);}}public static int kmpSearch(String text, String pattern) {int[] next = computeLPSArray(pattern);int i = 0; // text的指针int j = 0; // pattern的指针while (i < text.length()) {if (text.charAt(i) == pattern.charAt(j)) { // char匹配，都后移i++;j++;if (j == pattern.length()) {return i - j; // string匹配成功，返回起始位置}} else {if (j != 0) { // char匹配失败，pattern回退到上一个匹配的位置j = next[j - 1];} else { // (j == 0) 字符串第一个就匹配失败，直接后移i++;}}}return -1; // 匹配失败}public static int[] computeLPSArray(String pattern) {int[] next = new int[pattern.length()];int len = 0; // 最长公共前后缀的长度int i = 1; // pattern的指针while (i < pattern.length()) {if (pattern.charAt(i) == pattern.charAt(len)) {len++;next[i] = len;i++;} else {if (len != 0) {len = next[len - 1]; // 回退到前一个匹配的位置} else {next[i] = 0;i++;}}}return next;}public static int[] bruteComputeLPSArray(String pattern) {int[] lps = new int[pattern.length()];int len = 0;for (int i = 1; i <= pattern.length() - 1; i++) {if (pattern.charAt(i) == pattern.charAt(len)) {len++;lps[i] = len;} else {if (len != 0) {len = lps[len - 1];i--;} else {lps[i] = 0;}}}return lps;}
}