文章目录
- 前置知识
- 435. 无重叠区间
- 题目描述
- 参考<452. 用最少数量的箭引爆气球>, 间接求解
- 直接求"重叠区间数量"
- 763.划分字母区间
- 题目描述
- 贪心 - 建立"最后一个当前字母"数组
- 优化marker创建的过程
- 56. 合并区间
- 题目描述
- 解题思路
- 代码
- ① 如果有重合就合并到ans.back()里面
- ② 直接在intervals上操作(非常麻烦其实)
- ③ 整一个current数组来操作
- 总结
前置知识
参考前文
参考文章:
LeetCode刷题笔记【23】:贪心算法专题-1(分发饼干、摆动序列、最大子序和)
LeetCode刷题笔记【24】:贪心算法专题-2(买卖股票的最佳时机II、跳跃游戏、跳跃游戏II)
LeetCode刷题笔记【25】:贪心算法专题-3(K次取反后最大化的数组和、加油站、分发糖果)
LeetCode刷题笔记【26】:贪心算法专题-4(柠檬水找零、根据身高重建队列、用最少数量的箭引爆气球)
435. 无重叠区间
题目描述
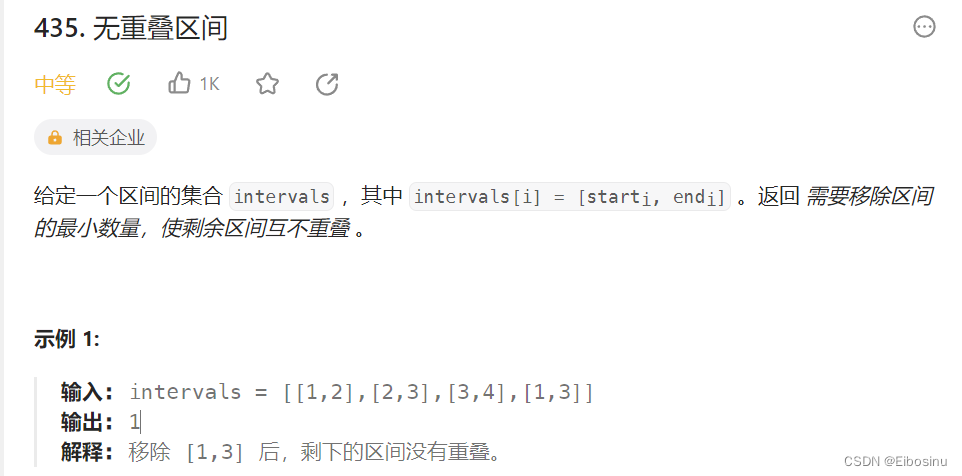
LeetCode链接:https://leetcode.cn/problems/non-overlapping-intervals/description/
参考<452. 用最少数量的箭引爆气球>, 间接求解
思路: 让我们求要移除多少区间, 从而让剩下的区间不重叠
那我们参考<452. 用最少数量的箭引爆气球>, 进行修改
引爆气球这一题中, 每一箭都代表一个"重叠区间组", 那么用 总区间数-箭数, 就得到多余的重复区间数量了
class Solution {
public:int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.empty()) return 0;int ans=1;sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b){return a[0] < b[0];});for(int i=1; i<intervals.size(); ++i){if(intervals[i][0] >= intervals[i-1][1]){ans++;}else{intervals[i][1] = min(intervals[i][1], intervals[i-1][1]);}}return intervals.size()-ans;}
};直接求"重叠区间数量"
直接求"重叠区间数量"
class Solution {
public:int eraseOverlapIntervals(vector<vector<int>>& intervals) {if(intervals.empty()) return 0;int count=0;sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b){return a[0] < b[0];});for(int i=1; i<intervals.size(); ++i){if(intervals[i][0] >= intervals[i-1][1]){continue;}else{count ++;intervals[i][1] = min(intervals[i][1], intervals[i-1][1]);}}return count;}
};
763.划分字母区间
题目描述
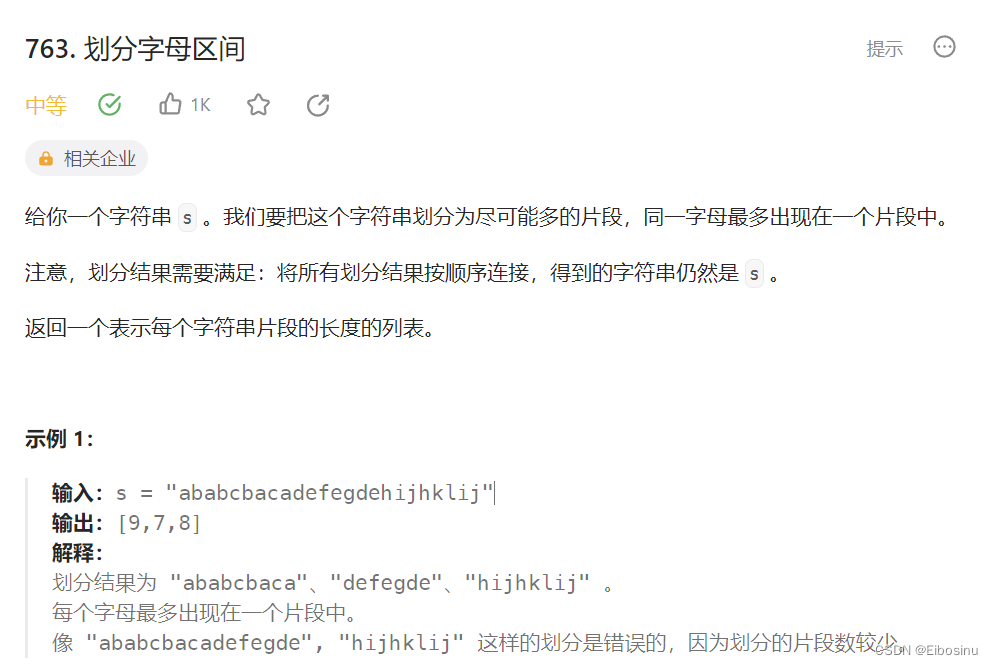
LeetCode链接:https://leetcode.cn/problems/partition-labels/description/
贪心 - 建立"最后一个当前字母"数组
参考<代>: 在真正开始遍历之前, 先建立一个vector<int> marker数组
marker[i]存储s[i]最远的下一个相同字母在哪一位
然后遍历的时候, 比如从i, 跳到了j, 那么下一个区间就从j开始
但是除此之外, 在第一次的i~j之间, 如果某个k的marker[k]>j, 那么j就要更新为marker[k]
class Solution {
public:vector<int> partitionLabels(string s) {vector<int> marker(s.size());for(int i=0; i<s.size(); ++i){char c = s[i];int j=s.size()-1;while(s[j] != s[i])j--;marker[i] = j;}// for(int i : marker)// cout << i << " " ;vector<int> ans;int left=0, right=0;for(int i=0; i<s.size(); ++i){right = max(right, marker[i]);if(i==right){ans.push_back(right-left+1);left = i+1;}}return ans;}
};
优化marker创建的过程
干菜这样做没问题, 但是在建立marker数组的时候可以更优雅
class Solution {
public:vector<int> partitionLabels(string s) {vector<int> marker(27);for(int i=0; i<s.size(); ++i){marker[s[i]-'a'] = i;}// for(int i : marker)// cout << i << " " ;vector<int> ans;int left=0, right=0;for(int i=0; i<s.size(); ++i){right = max(right, marker[s[i]-'a']);if(i==right){ans.push_back(right-left+1);left = i+1;}}return ans;}
};
56. 合并区间
题目描述
截图
LeetCode链接:xxx(记得加点击跳转链接)
解题思路
思路和<452. 用最少数量的箭引爆气球>以及<435. 无重叠区间>一样
都是先sort, 然后倒腾右边界(依次遍历, 如果有重叠就合并, 没有重叠就加入ans)
相比于前面两道例题, 没有合并后右边界取min的思维拐弯, 其实难度是降低的, 但还是要注意, 右边界要取cur和cpr的max
这里的"有重叠就合并", 一方面可以先在ans中加入一个区间, 然后和ans.back()合并
也可以直接在intervals上操作
甚至可以单独拎一个current数组出来进行操作
以下将分别展示这三种做法:
代码
① 如果有重合就合并到ans.back()里面
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b){return a[0] < b[0];});vector<vector<int>> ans;ans.push_back(intervals[0]);for(int i=1; i<intervals.size(); ++i){if(intervals[i][0] <= ans.back()[1]){// 一方面注意这里不是intervals[i-1], 而是ans.back()ans.back()[1] = max(intervals[i][1], ans.back()[1]);// 另一方面要注意, 这里原先的ans.back()的右侧边界可能还更大}else{ans.push_back(intervals[i]);}}return ans;}
};
② 直接在intervals上操作(非常麻烦其实)
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b){return a[0] < b[0];});vector<vector<int>> ans;for(int i=0; i<intervals.size()-1; ++i){if(intervals[i][1] < intervals[i+1][0]){ans.push_back(intervals[i]);}else{intervals[i+1][0] = min(intervals[i+1][0], intervals[i][0]);intervals[i+1][1] = max(intervals[i+1][1], intervals[i][1]);}}ans.push_back(intervals.back());return ans;}
};
③ 整一个current数组来操作
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(), intervals.end(), [](vector<int>& a, vector<int>& b){return a[0] < b[0];});vector<vector<int>> ans;vector<int> cur=intervals[0];for(vector<int>& interval : intervals){if(interval[0] > cur[1]){//么有重合ans.push_back(cur);cur = interval;}else{cur[1] = max(cur[1], interval[1]);}}ans.push_back(cur);return ans;}
};
总结
今天三道题, 可以和昨天的最后一道题结合来看, 都是区间操作的题目.
今天的第二题也可以用回溯来做, 但是回溯毕竟是遍历, 时间复杂度高.
这些区间操作题目可以提炼出以下操作方式和注意点
- 先sort, 再遍历操作 (如果按照左边界sort, 那么就操作右边界(反之亦可));
- 遍历操作过程中, 判断前后有无重合, 分类讨论操作;
- 如果是要求重叠区间类问题, 那么对右边界, 要转换为当前区间和新区间的min
- 如果是要求合并区间的问题, 那么对右边界, 要转换为当前区间和新区间的max(不能简单地认为新区间的右边界>当前区间的右边界, 可能是当前区间大到包含了新区间)
本文参考:
无重叠区间
划分字母区间
合并区间



![[开学季]ChatPaper全流程教程](https://img-blog.csdnimg.cn/c391263913a147a1979e6597c6bb3166.png)