代码更新地址：https://github.com/fengdu78/WZU-machine-learning-course

代码修改并注释：黄海广，haiguang2000@wzu.edu.cn

1．分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if-then规则的集合，也可以看作是定义在特征空间划分上的类的条件概率分布。

2．决策树学习旨在构建一个与训练数据拟合很好，并且复杂度小的决策树。因为从可能的决策树中直接选取最优决策树是NP完全问题。现实中采用启发式方法学习次优的决策树。

决策树学习算法包括3部分：特征选择、树的生成和树的剪枝。常用的算法有ID3、
C4.5和CART。

3．特征选择的目的在于选取对训练数据能够分类的特征。特征选择的关键是其准则。常用的准则如下：

（1）样本集合$D$对特征$A$的信息增益（ID3）

$$g(D,A)=H(D)-H(D|A)$$

$$H(D)=-\sum _{k=1}^K\frac{\left|C_k\right|}{|D|}{\log }_2\frac{\left|C_k\right|}{|D|}$$

$$H(D|A)=\sum _{i=1}^n\frac{\left|D_i\right|}{|D|}H\left(D_i\right)$$

其中，$H(D)$是数据集$D$的熵，$H(D_i)$是数据集$D_i$的熵，$H(D|A)$是数据集$D$对特征$A$的条件熵。 $D_i$是$D$中特征$A$取第$i$个值的样本子集，$C_k$是$D$中属于第$k$类的样本子集。$n$是特征$A$取 值的个数，$K$是类的个数。

（2）样本集合$D$对特征$A$的信息增益比（C4.5）

$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$

其中，$g(D,A)$是信息增益，$H(D)$是数据集$D$的熵。

（3）样本集合$D$的基尼指数（CART）

$$\mathrm{Gini}(D)=1-\sum _{k=1}^K{\left(\frac{\left|C_k\right|}{|D|}\right)}^2$$

特征$A$条件下集合$D$的基尼指数：

$$\mathrm{Gini}(D,A)=\frac{\left|D_1\right|}{|D|}\mathrm{Gini}\left(D_1\right)+\frac{\left|D_2\right|}{|D|}\mathrm{Gini}\left(D_2\right)$$

4．决策树的生成。通常使用信息增益最大、信息增益比最大或基尼指数最小作为特征选择的准则。决策树的生成往往通过计算信息增益或其他指标，从根结点开始，递归地产生决策树。这相当于用信息增益或其他准则不断地选取局部最优的特征，或将训练集分割为能够基本正确分类的子集。

5．决策树的剪枝。由于生成的决策树存在过拟合问题，需要对它进行剪枝，以简化学到的决策树。决策树的剪枝，往往从已生成的树上剪掉一些叶结点或叶结点以上的子树，并将其父结点或根结点作为新的叶结点，从而简化生成的决策树。

导入包：

import numpy as np
import pandas as pd
import math
from math import log

创建数据

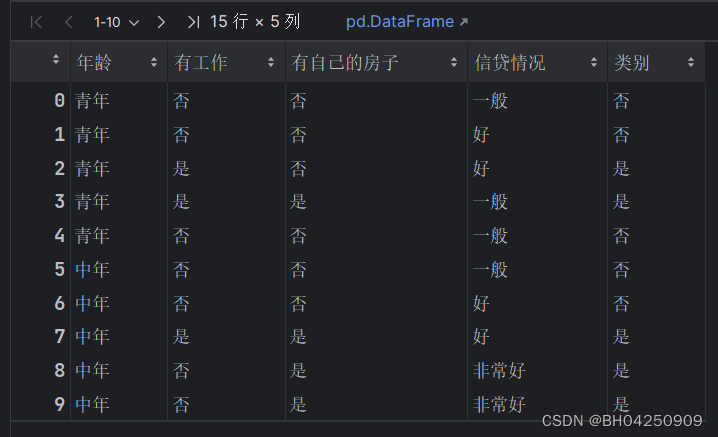
def create_data():datasets = [['青年', '否', '否', '一般', '否'],['青年', '否', '否', '好', '否'],['青年', '是', '否', '好', '是'],['青年', '是', '是', '一般', '是'],['青年', '否', '否', '一般', '否'],['中年', '否', '否', '一般', '否'],['中年', '否', '否', '好', '否'],['中年', '是', '是', '好', '是'],['中年', '否', '是', '非常好', '是'],['中年', '否', '是', '非常好', '是'],['老年', '否', '是', '非常好', '是'],['老年', '否', '是', '好', '是'],['老年', '是', '否', '好', '是'],['老年', '是', '否', '非常好', '是'],['老年', '否', '否', '一般', '否'],]labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']# 返回数据集和每个维度的名称return datasets, labels

datasets, labels = create_data()

train_data = pd.DataFrame(datasets, columns=labels)

train_data

熵

# 计算给定数据集的熵（信息熵）
def calc_ent(datasets):# 计算数据集的长度data_length = len(datasets)# 统计数据集中每个类别的出现次数label_count = {}for i in range(data_length):# 获取每个样本的标签label = datasets[i][-1]# 如果该类别不在label_count中，则添加到label_count中if label not in label_count:label_count[label] = 0# 统计该类别的出现次数label_count[label] += 1# 计算熵ent = -sum([(p / data_length) * log(p / data_length, 2)for p in label_count.values()])return ent

条件熵

# 计算给定数据集在指定特征上的条件熵
def cond_ent(datasets, axis=0):# 计算数据集的长度data_length = len(datasets)# 使用字典feature_sets存储在指定特征上的不同取值对应的样本集合feature_sets = {}for i in range(data_length):# 获取每个样本在指定特征上的取值feature = datasets[i][axis]# 如果该取值不在feature_sets中，则添加到feature_sets中if feature not in feature_sets:feature_sets[feature] = []# 将该样本添加到对应取值的样本集合中feature_sets[feature].append(datasets[i])# 计算条件熵cond_ent = sum([(len(p) / data_length) * calc_ent(p)for p in feature_sets.values()])return cond_ent

calc_ent(datasets)

0.9709505944546686

信息增益

#计算信息增益
def info_gain(ent, cond_ent):# 信息增益等于熵减去条件熵return ent - cond_ent

#使用信息增益选择最佳特征作为根节点特征进行决策树的训练
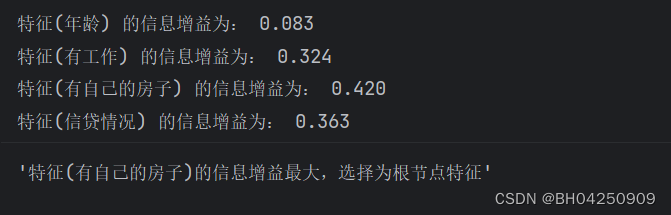
def info_gain_train(datasets):# 计算特征的数量count = len(datasets[0]) - 1# 计算整个数据集的熵ent = calc_ent(datasets)# 存储每个特征的信息增益best_feature = []for c in range(count):# 计算每个特征的条件熵c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))# 将特征及其对应的信息增益存入best_feature列表中best_feature.append((c, c_info_gain))# 输出每个特征的信息增益print('特征({}) 的信息增益为： {:.3f}'.format(labels[c], c_info_gain))# 找到信息增益最大的特征best_ = max(best_feature, key=lambda x: x[-1])# 返回信息增益最大的特征作为根节点特征return '特征({})的信息增益最大，选择为根节点特征'.format(labels[best_[0]])

info_gain_train(np.array(datasets))

利用ID3算法生成决策树

# 定义节点类 二叉树
class Node:def __init__(self, root=True, label=None, feature_name=None, feature=None):self.root = rootself.label = labelself.feature_name = feature_nameself.feature = featureself.tree = {}self.result = {'label:': self.label,'feature': self.feature,'tree': self.tree}def __repr__(self):return '{}'.format(self.result)def add_node(self, val, node):self.tree[val] = nodedef predict(self, features):if self.root is True:return self.labelreturn self.tree[features[self.feature]].predict(features)class DTree:def __init__(self, epsilon=0.1):self.epsilon = epsilonself._tree = {}# 熵@staticmethoddef calc_ent(datasets):data_length = len(datasets)label_count = {}for i in range(data_length):label = datasets[i][-1]if label not in label_count:label_count[label] = 0label_count[label] += 1ent = -sum([(p / data_length) * log(p / data_length, 2)for p in label_count.values()])return ent# 经验条件熵def cond_ent(self, datasets, axis=0):data_length = len(datasets)feature_sets = {}for i in range(data_length):feature = datasets[i][axis]if feature not in feature_sets:feature_sets[feature] = []feature_sets[feature].append(datasets[i])cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)for p in feature_sets.values()])return cond_ent# 信息增益@staticmethoddef info_gain(ent, cond_ent):return ent - cond_entdef info_gain_train(self, datasets):count = len(datasets[0]) - 1ent = self.calc_ent(datasets)best_feature = []for c in range(count):c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))best_feature.append((c, c_info_gain))# 比较大小best_ = max(best_feature, key=lambda x: x[-1])return best_def train(self, train_data):"""input:数据集D(DataFrame格式)，特征集A，阈值etaoutput:决策树T"""_, y_train, features = train_data.iloc[:, :-1], train_data.iloc[:,-1], train_data.columns[:-1]# 1,若D中实例属于同一类Ck，则T为单节点树，并将类Ck作为结点的类标记，返回Tif len(y_train.value_counts()) == 1:return Node(root=True, label=y_train.iloc[0])# 2, 若A为空，则T为单节点树，将D中实例树最大的类Ck作为该节点的类标记，返回Tif len(features) == 0:return Node(root=True,label=y_train.value_counts().sort_values(ascending=False).index[0])# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征max_feature, max_info_gain = self.info_gain_train(np.array(train_data))max_feature_name = features[max_feature]# 4,Ag的信息增益小于阈值eta,则置T为单节点树，并将D中是实例数最大的类Ck作为该节点的类标记，返回Tif max_info_gain < self.epsilon:return Node(root=True,label=y_train.value_counts().sort_values(ascending=False).index[0])# 5,构建Ag子集node_tree = Node(root=False, feature_name=max_feature_name, feature=max_feature)feature_list = train_data[max_feature_name].value_counts().indexfor f in feature_list:sub_train_df = train_data.loc[train_data[max_feature_name] ==f].drop([max_feature_name], axis=1)# 6, 递归生成树sub_tree = self.train(sub_train_df)node_tree.add_node(f, sub_tree)# pprint.pprint(node_tree.tree)return node_treedef fit(self, train_data):self._tree = self.train(train_data)return self._treedef predict(self, X_test):return self._tree.predict(X_test)

datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)

tree

{‘label:’: None, ‘feature’: 2, ‘tree’: {‘否’: {‘label:’: None, ‘feature’: 1, ‘tree’: {‘否’: {‘label:’: ‘否’, ‘feature’: None, ‘tree’: {}}, ‘是’: {‘label:’: ‘是’, ‘feature’: None, ‘tree’: {}}}}, ‘是’: {‘label:’: ‘是’, ‘feature’: None, ‘tree’: {}}}}

dt.predict(['老年', '否', '否', '一般'])

‘否’

Scikit-learn实例

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter

使用Iris数据集，我们可以构建如下树：

#data
def create_data():iris = load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)df['label'] = iris.targetdf.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']data = np.array(df.iloc[:100, [0, 1, -1]])# print(data)return data[:, :2], data[:, -1],iris.feature_names[0:2]X, y,feature_name= create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

决策树分类

from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz
from sklearn import treeclf = DecisionTreeClassifier()
clf.fit(X_train, y_train,)clf.score(X_test, y_test)

0.9

一旦经过训练，就可以用 plot_tree函数绘制树：

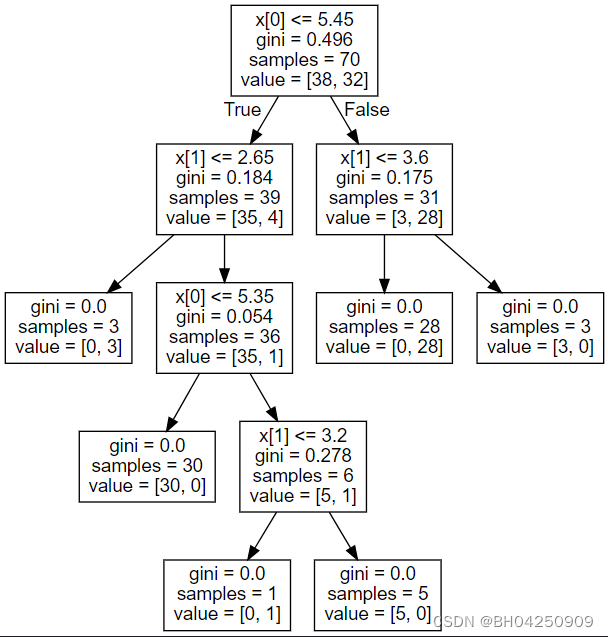
tree.plot_tree(clf) 

[Text(0.5, 0.9, ‘x[0] <= 5.45\ngini = 0.496\nsamples = 70\nvalue = [38, 32]’),
Text(0.25, 0.7, ‘x[1] <= 2.65\ngini = 0.184\nsamples = 39\nvalue = [35, 4]’),
Text(0.125, 0.5, ‘gini = 0.0\nsamples = 3\nvalue = [0, 3]’),
Text(0.375, 0.5, ‘x[0] <= 5.35\ngini = 0.054\nsamples = 36\nvalue = [35, 1]’),
Text(0.25, 0.3, ‘gini = 0.0\nsamples = 30\nvalue = [30, 0]’),
Text(0.5, 0.3, ‘x[1] <= 3.2\ngini = 0.278\nsamples = 6\nvalue = [5, 1]’),
Text(0.375, 0.1, ‘gini = 0.0\nsamples = 1\nvalue = [0, 1]’),
Text(0.625, 0.1, ‘gini = 0.0\nsamples = 5\nvalue = [5, 0]’),
Text(0.75, 0.7, ‘x[1] <= 3.6\ngini = 0.175\nsamples = 31\nvalue = [3, 28]’),
Text(0.625, 0.5, ‘gini = 0.0\nsamples = 28\nvalue = [0, 28]’),
Text(0.875, 0.5, ‘gini = 0.0\nsamples = 3\nvalue = [3, 0]’)]

也可以导出树

tree_pic = export_graphviz(clf, out_file="mytree.pdf")
with open('mytree.pdf') as f:dot_graph = f.read()

graphviz.Source(dot_graph)

或者，还可以使用函数 export_text以文本格式导出树。此方法不需要安装外部库，而且更紧凑：

from sklearn.tree import export_text

r = export_text(clf)

print(r)

|— feature_0 <= 5.45
| |— feature_1 <= 2.65
| | |— class: 1.0
| |— feature_1 > 2.65
| | |— feature_0 <= 5.35
| | | |— class: 0.0
| | |— feature_0 > 5.35
| | | |— feature_1 <= 3.20
| | | | |— class: 1.0
| | | |— feature_1 > 3.20
| | | | |— class: 0.0
|— feature_0 > 5.45
| |— feature_1 <= 3.60
| | |— class: 1.0
| |— feature_1 > 3.60
| | |— class: 0.0

决策树回归

import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))

# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)# Predict
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)# Plot the results
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue", label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

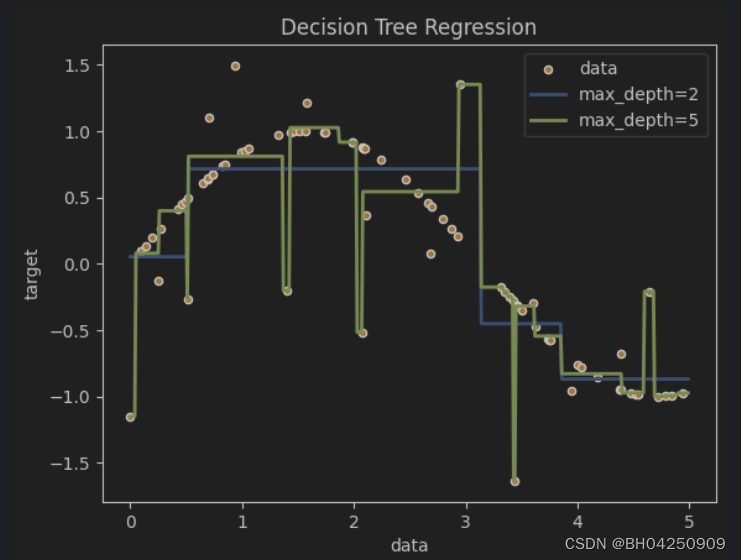
Scikit-learn 的决策树参数

DecisionTreeClassifier(criterion=“gini”,
splitter=“best”,
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.,
max_features=None,
random_state=None,
max_leaf_nodes=None,
min_impurity_decrease=0.,
min_impurity_split=None,
class_weight=None,
presort=False)

参数含义：
1.criterion:string, optional (default=“gini”)
(1).criterion=‘gini’,分裂节点时评价准则是Gini指数。
(2).criterion=‘entropy’,分裂节点时的评价指标是信息增益。
2.max_depth:int or None, optional (default=None)。指定树的最大深度。
如果为None，表示树的深度不限。直到所有的叶子节点都是纯净的，即叶子节点
中所有的样本点都属于同一个类别。或者每个叶子节点包含的样本数小于min_samples_split。
3.splitter:string, optional (default=“best”)。指定分裂节点时的策略。
(1).splitter=‘best’,表示选择最优的分裂策略。
(2).splitter=‘random’,表示选择最好的随机切分策略。
4.min_samples_split:int, float, optional (default=2)。表示分裂一个内部节点需要的做少样本数。
(1).如果为整数，则min_samples_split就是最少样本数。
(2).如果为浮点数(0到1之间)，则每次分裂最少样本数为ceil(min_samples_split * n_samples)
5.min_samples_leaf: int, float, optional (default=1)。指定每个叶子节点需要的最少样本数。
(1).如果为整数，则min_samples_split就是最少样本数。
(2).如果为浮点数(0到1之间)，则每个叶子节点最少样本数为ceil(min_samples_leaf * n_samples)
6.min_weight_fraction_leaf:float, optional (default=0.)
指定叶子节点中样本的最小权重。
7.max_features:int, float, string or None, optional (default=None).
搜寻最佳划分的时候考虑的特征数量。
(1).如果为整数，每次分裂只考虑max_features个特征。
(2).如果为浮点数(0到1之间)，每次切分只考虑int(max_features * n_features)个特征。
(3).如果为’auto’或者’sqrt’,则每次切分只考虑sqrt(n_features)个特征
(4).如果为’log2’,则每次切分只考虑log2(n_features)个特征。
(5).如果为None,则每次切分考虑n_features个特征。
(6).如果已经考虑了max_features个特征，但还是没有找到一个有效的切分，那么还会继续寻找
下一个特征，直到找到一个有效的切分为止。
8.random_state:int, RandomState instance or None, optional (default=None)
(1).如果为整数，则它指定了随机数生成器的种子。
(2).如果为RandomState实例，则指定了随机数生成器。
(3).如果为None，则使用默认的随机数生成器。
9.max_leaf_nodes: int or None, optional (default=None)。指定了叶子节点的最大数量。
(1).如果为None,叶子节点数量不限。
(2).如果为整数，则max_depth被忽略。
10.min_impurity_decrease:float, optional (default=0.)
如果节点的分裂导致不纯度的减少(分裂后样本比分裂前更加纯净)大于或等于min_impurity_decrease，则分裂该节点。
加权不纯度的减少量计算公式为：
min_impurity_decrease=N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
其中N是样本的总数，N_t是当前节点的样本数，N_t_L是分裂后左子节点的样本数，
N_t_R是分裂后右子节点的样本数。impurity指当前节点的基尼指数，right_impurity指
分裂后右子节点的基尼指数。left_impurity指分裂后左子节点的基尼指数。
11.min_impurity_split:float
树生长过程中早停止的阈值。如果当前节点的不纯度高于阈值，节点将分裂，否则它是叶子节点。
这个参数已经被弃用。用min_impurity_decrease代替了min_impurity_split。
12.class_weight:dict, list of dicts, “balanced” or None, default=None
类别权重的形式为{class_label: weight}
(1).如果没有给出每个类别的权重，则每个类别的权重都为1。
(2).如果class_weight=‘balanced’，则分类的权重与样本中每个类别出现的频率成反比。
计算公式为：n_samples / (n_classes * np.bincount(y))
(3).如果sample_weight提供了样本权重(由fit方法提供)，则这些权重都会乘以sample_weight。
13.presort:bool, optional (default=False)
指定是否需要提前排序数据从而加速训练中寻找最优切分的过程。设置为True时，对于大数据集
会减慢总体的训练过程；但是对于一个小数据集或者设定了最大深度的情况下，会加速训练过程。

决策树调参

# 导入库
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor
from sklearn import metrics

# 导入数据集
X = datasets.load_iris()  # 以全部字典形式返回,有data,target,target_names三个键
data = X.data
target = X.target
name = X.target_names
x, y = datasets.load_iris(return_X_y=True)  # 能一次性取前2个
print(x.shape, y.shape)

(150, 4) (150,)

# 数据分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2,random_state=100)

# 用GridSearchCV寻找最优参数（字典）
param = {'criterion': ['gini'],'max_depth': [30, 50, 60, 100],'min_samples_leaf': [2, 3, 5, 10],'min_impurity_decrease': [0.1, 0.2, 0.5]
}
grid = GridSearchCV(DecisionTreeClassifier(), param_grid=param, cv=6)
grid.fit(x_train, y_train)
print('最优分类器:', grid.best_params_, '最优分数:', grid.best_score_)  # 得到最优的参数和分值

最优分类器: {‘criterion’: ‘gini’, ‘max_depth’: 50, ‘min_impurity_decrease’: 0.2, ‘min_samples_leaf’: 2} 最优分数: 0.9416666666666665

参考：

• https://github.com/fengdu78/lihang-code

• 李航. 统计学习方法[M]. 北京: 清华大学出版社,2019.

• https://scikit-learn.org