为了深入了解这些生物群体的生态特征,你们进行了大量的实地观察和数据采集。数组 arrayA 记录了各个生物群体数量数据,其中 arrayA[i] 表示第 i 个生物群体的数量。请返回一个数组 arrayB,该数组为基于数组 arrayA 中的数据计算得出的结果,其中 arrayB[i] 表示将第 i 个生物群体的数量从总体中排除后的其他数量的乘积。
示例 1:
输入:arrayA = [2, 4, 6, 8, 10]
输出:[1920, 960, 640, 480, 384]
- 我的原始人解法:首先如果没有 0,那就先得到每个数的乘积 x,然后最终结果
ans[i] = x/arrayA[i];如果只有一个 0,只需要计算出除了这个 0 以外其他数的乘积,否则就都是 0 了 -
public int[] statisticalResult(int[] nums) {int x = 1, zero = 0;for(int n:nums){if(n==0 && zero == 0){// 如果是第一个 0 我就暂且跳过这个 0 继续计算乘积// 这时为了应对数组中只有一个 0 的情况,为 0 的那个对应为除了 0 的乘积// 否则就不管你了,全为 0 吧zero++;continue;}x *= n;}int[] ans = new int[nums.length];for(int i=0;i<nums.length;i++){// 如果有 0 那只有是 0 那一位能为 x,只有一个 0 的话 x 还能为正数,否则就为 0if(zero > 0)ans[i] = nums[i]==0?x:0;// 为了防止 0 被作为被除数,所以就这样了else ans[i] = x/nums[i];}return ans;} - 他人题解:首先为了防止除 0,我们索性就只用乘法来解决。根据题意我们可以得到以下 B[i] 的计算公式,就是除了 A[i] 以外其他 A[x] 的乘积。比如
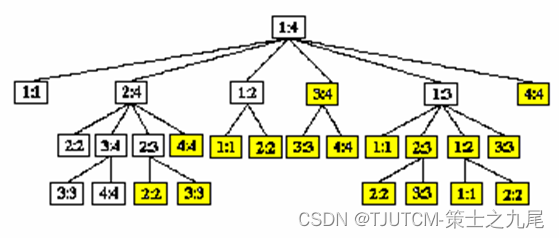
B[2] = A[0] x A[1] x A[3] x...,那么其实你也可以看做B[2] = A[0] x A[1] x A[2] x A[3] x...,只不过这个 A[2] 为 1,即B[i] = A[0] x A[1] x ... x A[i-1] x 1 * A[i+1]...,这也就是下表的由来。我们不着急直接计算,而是观察规律,你会发现可以分为两个三角
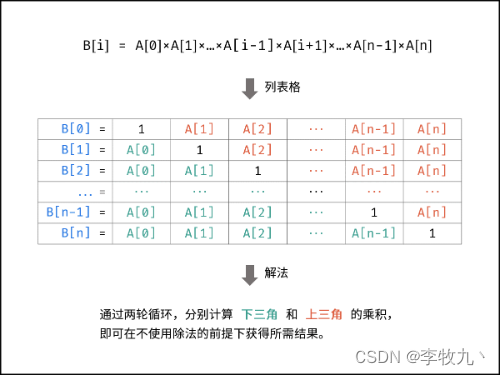
- 其中绿色那个三角的
- B[0] = 1
- B[1] = A[0]
- B[2] = A[0] x A[1]
- B[3] = A[0] x A[1] x A[2]
- 你发现没有,这个乘积貌似是可以迭代的,即 i 从 1开始,B[i] = B[i-1] x A[i-1]
- B[0] = 1
- B[1] = A[0] = B[0] x A[0]
- B[2] = A[0] x A[1] = B[1] x A[1]
- B[3] = A[0] x A[1] x A[2] = B[2] x A[2]
- 也就是我们只要以 1 为起点就能得到下三角的乘积了,也算是得到了每个 B[i] 的一半乘积
- 下三角我们也是同理从 1 开始迭代,之前顺着能直接用结果数组 B 来迭代,上三角得倒着来,我们原理还是不变,用一个 temp 来从 1 开始迭代好了,让他不断乘以 A[n],A[n-1]…
-
public int[] statisticalResult(int[] a) {int n = a.length;if(n == 0) return new int[0];int[] b = new int[n];b[0] = 1;int temp = 1;// 先得到 b[i] 的下三角乘积,也就是 b[i] 的一半乘积for(int i=1;i<n;i++){b[i] = b[i-1] * a[i-1];}// 对照上面的表看,迭代顺序为从下往上,// 所以先乘以 1,然后乘以 A[n],然后乘以 A[n]xA[n-1]...// 我们用 temp 来表示这个迭代的数for(int i=n-1;i>=0;i--){// b[i] 乘上自己的另一半乘积b[i] *= temp;temp *= a[i];}return b;}