📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

前言
希尔排序,作为一种高效的排序算法,更是在排序算法这个舞台上展现出了自己独特的魅力,听这个名字就感觉这个排序不简单,本篇文章我将带领大家深入了解希尔排序。
1. 排序算法
在数据世界中,排序算法是一种强大的工具,能够将混乱无序的数据变得井然有序,排序算法有很多种,最常见也是最常用的排序算法有8种,本期的主角是希尔排序。
1.1插入排序
希尔排序属于插入排序的一种,在理解希尔排序之前,我们需要先来了解一下插入排序的初阶——直接插入排序
1.1.1 直接插入排序
直接插入排序的原理非常好理解,举个例子:我们在完扑克牌时都会对牌的大小进行排序(也就是组成顺子)。

这就利用了直接直接插入排序,7和10比较,7小,7再和5比较,比5大,所以7就插入到10的前边。
直接插入排序,是一种简单直观的排序算法,它的基本思想是将一个待排序的元素插入到已经排好序的元素序列中的适当位置,从而得到一个新的、个数加一的有序序列。具体步骤如下:
- 将待排序序列第一个元素视为已排序序列,将其作为比较的基准。
- 从第二个元素开始,依次将每个元素插入到已排序序列中的适当位置。
- 每次插入一个元素时,都将该元素与已排序序列中的元素进行比较,找到合适的位置插入。
- 插入时,将已排序序列中比待插入元素大的元素向后移动一位,为待插入元素腾出位置。
- 重复步骤3和步骤4,直到将所有元素插入到已排序序列中。
过程如下图:
理解了基本原理,我们来进行代码实现,在写排序算法时我们可以先写一趟的逻辑。我们需要记录开始比较的位置,还要记录开始位置的后一个数据,例如当end=0时,我们需要记录end的后一个位置数据,从end开始一次向前移动并比较大小。如果tmp小于end位置的数据,那么,end位置的数据就向后移动一个位置。在这个过程中end要不断减减。具体代码如下:
int end = ;int tmp = arr[end + 1];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];}else{break;}end--;}arr[end + 1] = tmp;//找到比tmp大的数据后跳出循环插入到end的后边
}这也仅仅是一个数据插入的过程,接下来我们要搞定这个数组所有的元素。我们可以利用一个for循环,观察动图我们可以发现,end是逐个向后的。但我们需要考虑越界的问题,i要小于n-1,结束位置在最后的前一个位置。完整代码如下:
void InsertSort(int* arr,int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];}else{break;}end--;}arr[end + 1] = tmp;}
}1.1.2 希尔排序
由来
通过上述的插入排序过程我们可以发现,插入排序的时间复杂度不低,在局部有序的情况下,插入排序很优。但存在最坏的情况,就是逆序。逆序的情况下,它的时间复杂度不亚于冒泡排序。
为了防止出现较坏的情况,有位叫希尔的大佬对插入排序进行了优化,就是在插入排序之前进行预排序。所以希尔排序的过程就可分为两部分:
- 预排序
- 插入排序
过程
希尔排序(Shell Sort),也称为缩小增量排序,是插入排序的一种改进算法。它通过将待排序序列分割成若干子序列来进行排序,最终将整个序列排序。
希尔排序的基本思想是先将待排序序列按照一定的增量进行分组,对每个子序列进行插入排序,然后逐步缩小增量,再次进行分组和插入排序,直到增量为1,完成最后一次插入排序,整个序列就变成有序的。
预排序
上边说到按照增量进行分组,不好理解,我们可以理解为步数(gap),当gap为1的时候就是插入排序,gap为1就是相邻数据依次比较进行插入。当gap > 1时都是预排序,目的是让数组更接近于有序。
例如gap等于4,那进行比较时就是对相邻间隔为4的数据进行调整位置插入。如下图:
gap越小,数据就越接近有序。
1.1.3 希尔排序的实现
理解了预排序的原理,我们可以先来写一下预排序。
for (int i = 0; i < n - gap; i+=gap)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;
}这段代码看着是否很熟悉,当gap为1时,这段代码就是直接插入排序。这个是从第一个数据开始,将数组中距离为gap数据进行调整。
那么接下来还要从第二个数据开始,将距离为gap的数据进行调整。所以这里我们可以加一个循环,确保每个数据都能被调整。
for (int i = 0; i < gap; i++)
{for (int i = 0; i < n - gap; i+=gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;}
}这里我们可以优化一下,我们这样写:
for (int i = 0; i < n - gap; i++)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;
}大多数看到的书中都是这样写的,或许在之前学习中,很多同学不懂for循环这里为什么这样写。起初的逻辑是,调整完一组后,再调整下一组。那我们可不可以同时调整所有组?
我们先调整第一个数据和它距离为gap的数据,不急着将整组数据调整完,接着开始从第二个数据开始与它距离为gap的数据进行调整……
理解了这里,我们继续,上述的过程是在gap不变的情况下进行的,预排序的过程是不断的改变gap的值来进行预排序。gap越小预排序后数据越接近有序。
void ShellSort(int* a, int n)
{int gap = n;while (gap>1){gap = gap / 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];}else{break;}end -= gap;}a[end + gap] = tmp;}}
}我们可以先令gap等于n(数组的数据个数),然后使用while循环判断gap是否大于1,当gap > 1时都是预排序,进入while循环之后,gap就整除2。到这里希尔排序就实现了。任何一个大于2的数除2最后都等于1,除到最后gap等于2时进入while循环,先执行gap=gap/2,最后一次执行时就刚好是插入排序。
当然gap也不一定就除2,在一些书中也有这样的写法:gap=gap/3+1,除3是因为有人觉得gap/2进行预排序的次数太多了,但gap/3并不能保证除到最后,所以就有了这种写法:gap=gap/3+1。
2. 复杂度
了解了直接插入排序和希尔排序,那我们就来说一说它的复杂度问题,它们的空间复杂度都为O(1),重点就在它们的时间复杂度。
2.1 直接插入排序
直接插入排序的时间复杂度好说,假设有n个数据,第一次从第一个数据开始,最多比较1次,第二次从第二个数据开始,最多比较2次,第三个最多比较3次……
那么它的执行次数T=1+2+3+4+……+n-1,等差数列求和,T=(n-1+1)*n/2(首项加尾项乘以项数除以2)所以它的时间复杂度最差达到O(N^2)。
2.2 希尔排序
希尔排序的时间复杂度计算非常复杂,它的时间复杂度和gap有关。
当gap很大时,例如gap=n/3。整个数组逆序那么就有n/3组数据,每组数据最多比较3(1+2)次。
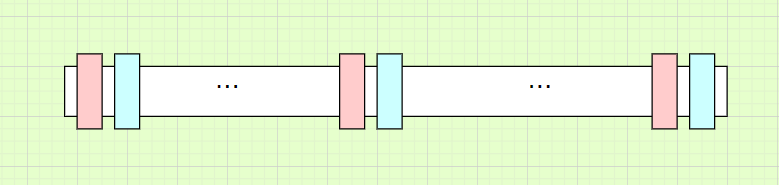
合计比较:n/3*3=n。
当gap等于n/9时,整个数组逆序,就会有n/9组数据,每组有9个数据,每组最多比较(1+2+3+4+5+6+7+8)次
合计比较:n/9*36=4n。
当gap很小时,如gap等于1时,就只有1组数据进行调整排序,此时的数据已经非常接近有序了,再进行调整,最差会比较n次,估算一下,合计:n
由此可以看出:希尔排序的性能图形为一个曲线函数。
希尔排序时间复杂度计算分析,以上内容为了解
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在很多书中给出的希尔排序的时间复杂度都不固定。在实际测试效果时,众多答案中,最符合的是O(N^1.3)。从这里就可以看出,希尔排序它非常的不稳。
总结
本篇文章主要介绍了希尔排序,希尔排序的时间复杂度与增量序列的选择有关,它是一种不稳定的排序算法,适用于中等规模的数据排序。希望本文对你有所帮助,最后,感谢阅读!