目录

第一题

题目来源

题目内容

解决方法

方法一：回溯算法

方法二：基于位运算的回溯

第二题

题目来源

题目内容

解决方法

方法一：动态规划

方法二：分治法 

方法三：前缀和数组

第三题

题目来源

题目内容

解决方法

方法一：模拟遍历

方法二：递归

方法三：方向转换法

方法四：螺旋填数法

---

第一题

题目来源

52. N 皇后 II - 力扣（LeetCode）

题目内容

解决方法

方法一：回溯算法

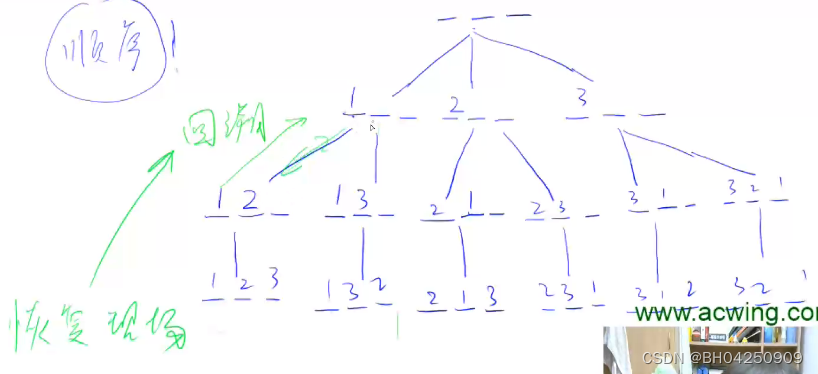
要解决N皇后问题，可以使用回溯算法。

回溯算法是一种通过试错的方式搜索所有可能解的算法。在每一步选择中，我们尝试放置一个皇后，并递归地处理剩下的部分。如果当前方案不能得到有效解，则撤销上一步的选择，回溯到上一层继续尝试其他选择。

具体步骤如下：

1. 定义一个长度为N的数组queens，用于存储每行皇后所在的列数。
2. 从第一行开始，依次遍历每一行。
3. 在当前行，尝试将皇后放置在每一列，判断是否满足条件。
   • 如果满足条件，则将该列标记为皇后所在的位置，并进入下一行进行递归。
   • 如果不满足条件，则继续尝试下一列。
4. 当遍历完最后一行时，说明找到了一组解决方案，计数器count加1。
5. 回溯到上一行，撤销当前行的选择，继续尝试下一列。
6. 当所有可能的选择都尝试完毕后，回溯结束。

在判断当前位置是否满足条件时，需要检查当前列、主对角线和副对角线上是否已经有其他皇后。如果存在冲突，则当前位置不可放置皇后。

最终，统计计数器count的值即为N皇后问题的不同解决方案数量。

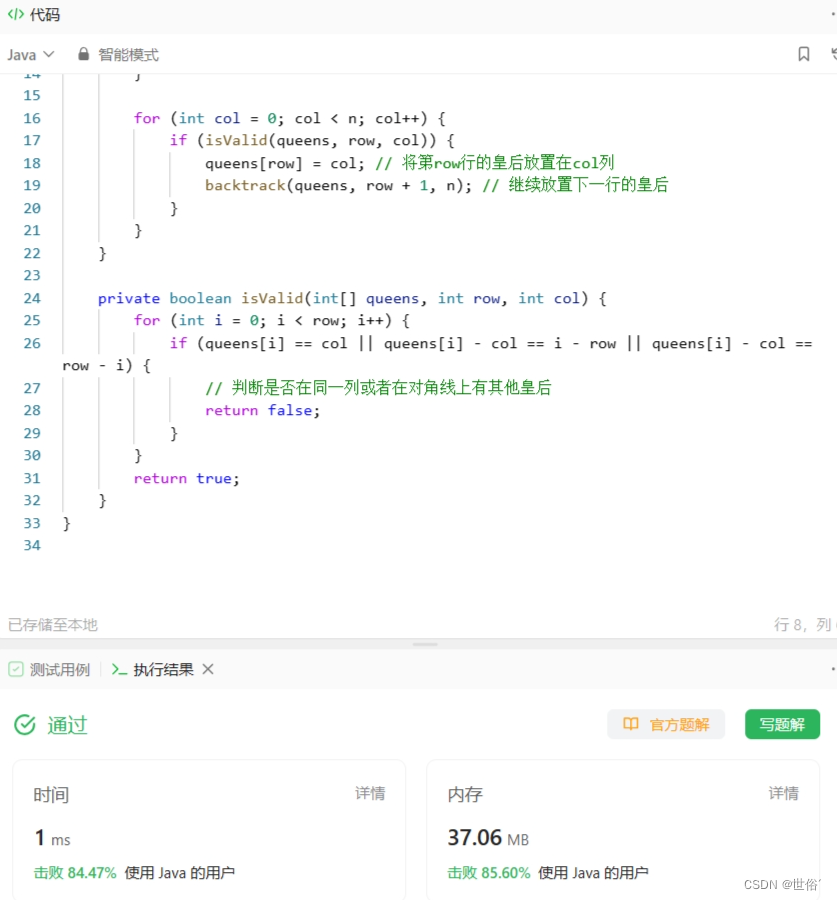
class Solution {int count = 0; // 解决方案的数量public int totalNQueens(int n) {int[] queens = new int[n]; // 用来存储每行皇后所在的列数backtrack(queens, 0, n);return count;}private void backtrack(int[] queens, int row, int n) {if (row == n) { // 找到一个解决方案count++;return;}for (int col = 0; col < n; col++) {if (isValid(queens, row, col)) {queens[row] = col; // 将第row行的皇后放置在col列backtrack(queens, row + 1, n); // 继续放置下一行的皇后}}}private boolean isValid(int[] queens, int row, int col) {for (int i = 0; i < row; i++) {if (queens[i] == col || queens[i] - col == i - row || queens[i] - col == row - i) {// 判断是否在同一列或者在对角线上有其他皇后return false;}}return true;}
}

复杂度分析：

• 时间复杂度：该解法使用回溯算法，在每一行中需要遍历N个位置。因此，总共有N行，复杂度为 O(N^N)。但是，由于N的取值范围非常小（1<=N<=9），因此实际运行效率很高。
• 空间复杂度：该解法只需要一个长为N的数组来记录每个皇后所在的列数，因此空间复杂度为O(N)。

综上所述，该解法的时间复杂度和空间复杂度都较小，可以快速地找到N皇后问题的所有解决方案。

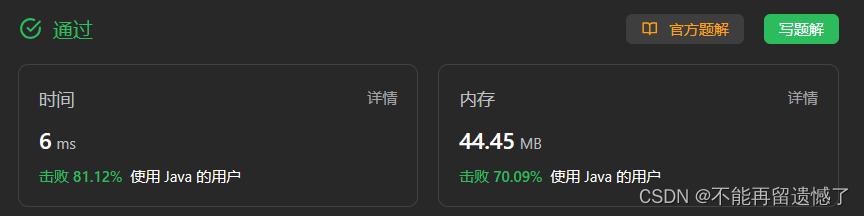
LeetCode运行结果：

方法二：基于位运算的回溯

位运算方法是一种巧妙的解决N皇后问题的算法，其基本思路如下：

1. 使用一个整数变量来表示每一行、每一列以及两个对角线的占用情况。

   • 对于每一行，整数的二进制表示中的某一位为1表示该位置已经被占用。
   • 对于每一列，整数的二进制表示中的某一位为1表示该列已经有皇后。
   • 对于主对角线（左上到右下方向）和副对角线（左下到右上方向），可以通过移位操作来表示。

2. 在回溯过程中，逐行放置皇后，并更新整数变量的占用情况。

   • 遍历当前行的每个位置，检查该位置是否可放置皇后。
   • 如果该位置对应的列、主对角线和副对角线都没有被占用，则进行递归调用。
   • 在递归调用之前，需要更新整数变量的占用情况，将相应的位置设置为已占用。

3. 当递归到最后一行时，找到一个合法解法，计数加一。

   • 在递归过程中，如果当前行达到了N，说明已经成功放置了N个皇后，找到一个合法解法，计数器加一。

4. 通过递归回溯的方式，遍历所有可能的放置方式。

这种位运算方法可以有效地判断皇后的位置是否冲突，且在求解过程中不需要额外的数据结构来存储棋盘状态。通过位运算的方式，可以在常数时间内进行判断和更新占用情况，从而大大提高了算法的效率。

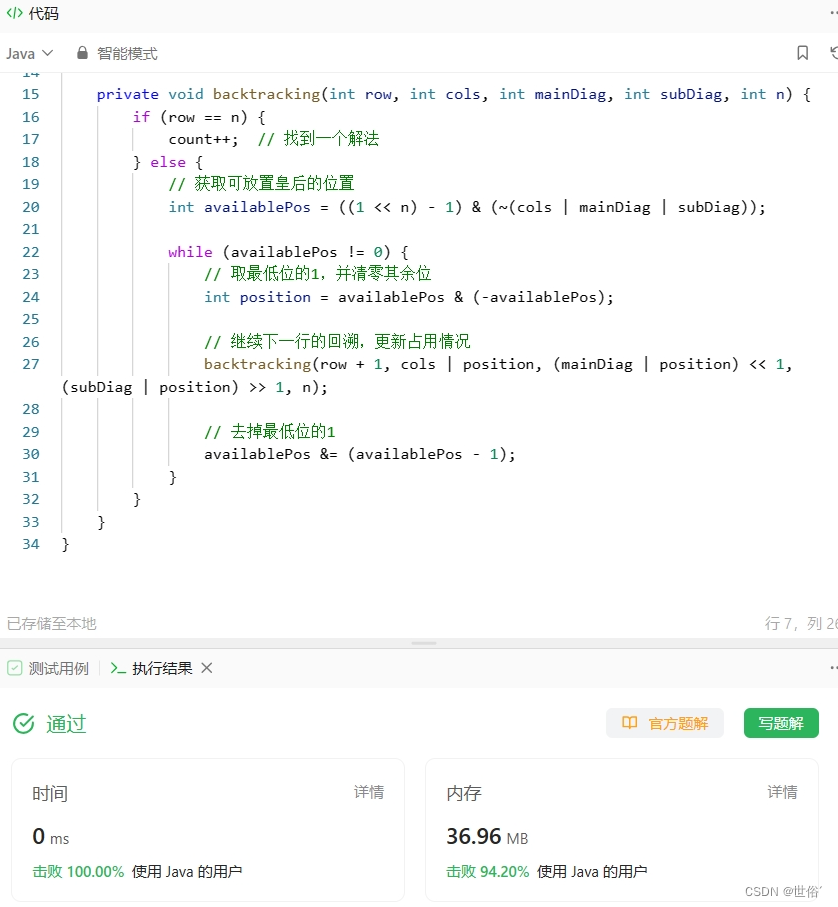
class Solution {
private int count;  // 解法计数器public int totalNQueens(int n) {// 初始化列、主对角线和副对角线的占用情况int cols = 0;int mainDiag = 0;int subDiag = 0;backtracking(0, cols, mainDiag, subDiag, n);return count;}private void backtracking(int row, int cols, int mainDiag, int subDiag, int n) {if (row == n) {count++;  // 找到一个解法} else {// 获取可放置皇后的位置int availablePos = ((1 << n) - 1) & (~(cols | mainDiag | subDiag));while (availablePos != 0) {// 取最低位的1，并清零其余位int position = availablePos & (-availablePos);// 继续下一行的回溯，更新占用情况backtracking(row + 1, cols | position, (mainDiag | position) << 1, (subDiag | position) >> 1, n);// 去掉最低位的1availablePos &= (availablePos - 1);}}}
}

复杂度分析：

• 时间复杂度： 在位运算方法中，回溯的过程是一个递归操作。在每一行中，需要遍历当前行的每个位置，然后进行递归调用。在最坏情况下，每个位置都需要进行递归调用。因此，时间复杂度可以表示为O(N!)，其中N是皇后的数量。
• 空间复杂度： 位运算方法的空间复杂度主要由递归调用时的内存消耗决定。在每个递归调用中，需要保存当前行、列、主对角线和副对角线的占用情况，以及递归过程中的其他临时变量。因此，空间复杂度可以表示为O(N)，其中N是皇后的数量。

综上所述，位运算方法解决N皇后问题的时间复杂度为O(N!)，空间复杂度为O(N)。该算法在较小的N值下可以快速求解N皇后问题，但随着N的增大，时间复杂度呈指数级增长，计算量会变得非常大。对于较大的N值，可能需要使用其他优化方法来降低计算的复杂度。

LeetCode运行结果：

第二题

题目来源

53. 最大子数组和 - 力扣（LeetCode）

题目内容

解决方法

方法一：动态规划

最大子数组和问题可以使用动态规划算法来解决。我们可以定义一个动态规划数组dp，其中dp[i]表示以第i个元素结尾的最大子数组和。

对于数组中的第i个元素，有两种情况：

1. 将第i个元素加入到前面的子数组中：如果dp[i-1]大于0，说明前面的子数组和对于当前元素是有贡献的，所以将第i个元素加入到前面的子数组中会使得子数组和更大。因此，dp[i] = dp[i-1] + nums[i]。
2. 第i个元素作为新的子数组的起点：如果dp[i-1]小于等于0，说明前面的子数组和对于当前元素没有贡献，所以舍弃前面的子数组，将第i个元素作为新的子数组的起点。因此，dp[i] = nums[i]。

通过以上的状态转移方程，我们可以计算出dp数组的每一个元素，然后找到其中的最大值maxSum，即得到最大子数组和。

最后，返回maxSum作为结果。

class Solution {public int maxSubArray(int[] nums) {int n = nums.length;int[] dp = new int[n]; // dp[i]表示以第i个元素结尾的最大子数组和dp[0] = nums[0];int maxSum = dp[0];for (int i = 1; i < n; i++) {dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);maxSum = Math.max(maxSum, dp[i]);}return maxSum;}
}

复杂度分析：

时间复杂度分析：

• 遍历数组的过程中，需要计算每个位置上以该元素结尾的最大子数组和。这一步的时间复杂度是O(n)，其中n是数组的长度。
• 在计算每个位置上的最大子数组和时，只需要比较当前元素和当前元素加上前面子数组和的结果。这是一个常数时间操作。
• 因此，整个算法的时间复杂度是O(n)。

空间复杂度分析：

• 只需要使用一个动态规划数组dp来保存计算过程中的中间结果。所以空间复杂度是O(n)，其中n是数组的长度。
• 注意，这里的空间复杂度是指额外使用的空间，不包括输入数组本身的空间。

综上所述，最大子数组和问题的解决方案的时间复杂度是O(n)，空间复杂度是O(n)。

LeetCode运行结果：

方法二：分治法 

除了动态规划之外，我们还可以使用分治法来解决最大子数组和问题。

分治法的基本思想是将问题划分为更小的子问题，并且递归地求解子问题。然后将子问题的结果合并起来得到原问题的结果。

对于最大子数组和问题，可以将数组划分为左右两个子数组，分别求解左子数组、右子数组和跨越中点的最大子数组和。最后将这三个结果中的最大值作为最终的结果。

具体步骤如下：

1. 如果数组的长度为1，则最大子数组和就是数组中的唯一元素。
2. 将数组等分为左右两部分，分别对左右子数组递归地求解最大子数组和，得到左子数组的最大子数组和leftSum和右子数组的最大子数组和rightSum。
3. 计算跨越中点的最大子数组和crossSum：
   • 从中点开始向左遍历，找到以中点为起点的最大子数组和leftCrossSum。
   • 从中点的下一个位置开始向右遍历，找到以中点+1为起点的最大子数组和rightCrossSum。
   • 跨越中点的最大子数组和crossSum = leftCrossSum + rightCrossSum。
4. 返回leftSum、rightSum和crossSum中的最大值作为最终的结果。

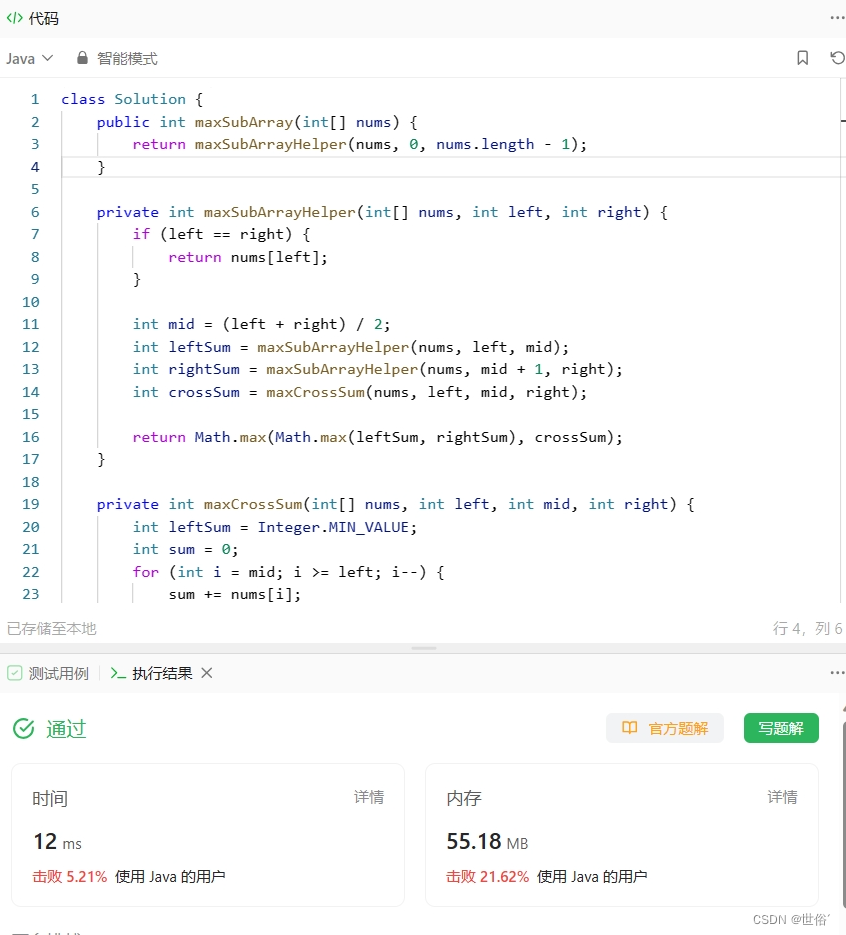
class Solution {public int maxSubArray(int[] nums) {return maxSubArrayHelper(nums, 0, nums.length - 1);}private int maxSubArrayHelper(int[] nums, int left, int right) {if (left == right) {return nums[left];}int mid = (left + right) / 2;int leftSum = maxSubArrayHelper(nums, left, mid);int rightSum = maxSubArrayHelper(nums, mid + 1, right);int crossSum = maxCrossSum(nums, left, mid, right);return Math.max(Math.max(leftSum, rightSum), crossSum);}private int maxCrossSum(int[] nums, int left, int mid, int right) {int leftSum = Integer.MIN_VALUE;int sum = 0;for (int i = mid; i >= left; i--) {sum += nums[i];leftSum = Math.max(leftSum, sum);}int rightSum = Integer.MIN_VALUE;sum = 0;for (int i = mid + 1; i <= right; i++) {sum += nums[i];rightSum = Math.max(rightSum, sum);}return leftSum + rightSum;}
}

复杂度分析：

• 时间复杂度是O(n log n)，其中n是数组的长度。因为每次递归都将数组划分为两个子数组，并且需要线性时间来计算跨越中点的最大子数组和。总共有log n层递归，每层的时间复杂度是O(n)，所以总的时间复杂度是O(n log n)。
• 空间复杂度是O(log n)，其中n是数组的长度。每次递归都需要额外的空间来保存函数调用的上下文，递归深度是log n，所以空间复杂度是O(log n)。

LeetCode运行结果：

方法三：前缀和数组

使用前缀和数组解决最大子数组和问题的思路与算法如下：

1. 首先，构建一个前缀和数组prefixSum，用于记录原始数组中每个位置之前所有元素的和。具体的操作如下：

   • 初始化一个长度为n+1的前缀和数组prefixSum，其中n为原始数组的长度。
   • 遍历原始数组nums，计算每个位置i之前所有元素的和，并将其存入prefixSum[i+1]中。即prefixSum[i+1] = nums[0] + nums[1] + ... + nums[i]。
   • 这样，prefixSum数组中的第i个元素表示原始数组中前i个元素的和。

2. 接下来，遍历前缀和数组prefixSum，同时维护两个变量maxSum和minPrefixSum，用于记录当前最大子数组和和当前最小前缀和。具体的操作如下：

   • 初始化maxSum为负无穷大，minPrefixSum为0。
   • 遍历前缀和数组prefixSum的每个元素prefixSum[i]：
     • 更新maxSum，取当前prefixSum[i]减去minPrefixSum的差值与maxSum的较大值。
     • 更新minPrefixSum，取当前prefixSum[i]与minPrefixSum的较小值。

3. 最后，返回maxSum作为最大子数组和的结果。

这个算法的关键在于利用前缀和数组来计算子数组的和，避免了重复计算。通过维护最大子数组和和最小前缀和，可以在遍历过程中动态更新并得到最终结果。

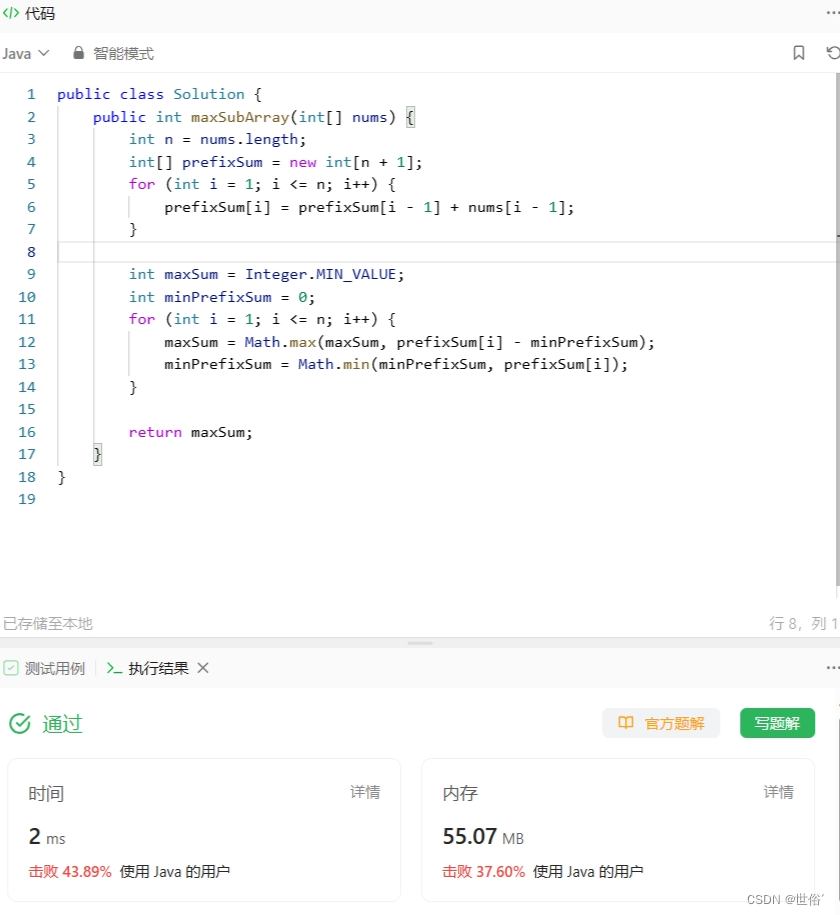
public class Solution {public int maxSubArray(int[] nums) {int n = nums.length;int[] prefixSum = new int[n + 1];for (int i = 1; i <= n; i++) {prefixSum[i] = prefixSum[i - 1] + nums[i - 1];}int maxSum = Integer.MIN_VALUE;int minPrefixSum = 0;for (int i = 1; i <= n; i++) {maxSum = Math.max(maxSum, prefixSum[i] - minPrefixSum);minPrefixSum = Math.min(minPrefixSum, prefixSum[i]);}return maxSum;}
}

复杂度分析：

• 时间复杂度：构建前缀和数组需要遍历一次原始数组，时间复杂度为O(n)。然后在计算最大子数组和时，需要再次遍历一次前缀和数组，时间复杂度也是O(n)。因此，总体时间复杂度为O(n)。
• 空间复杂度：需要额外的空间存储前缀和数组，空间复杂度为O(n)。

综上所述，使用前缀和数组解决最大子数组和问题的时间复杂度为O(n)，空间复杂度为O(n)。

需要注意的是，虽然使用前缀和数组的时间复杂度与动态规划的时间复杂度相同，但两种方法的实现思路和具体代码略有不同。前缀和数组适用于需要频繁查询子数组和的场景，而动态规划适用于需要记录具体的子数组位置的场景。根据实际需求选择合适的方法。

LeetCode运行结果：

第三题

题目来源

54. 螺旋矩阵 - 力扣（LeetCode）

题目内容

解决方法

方法一：模拟遍历

思路与算法：

该问题可以通过模拟遍历的方式来解决。我们使用四个变量rowStart、rowEnd、colStart、colEnd来表示当前要遍历的子矩阵的边界位置。

初始化时，rowStart为0，rowEnd为矩阵的行数减1，colStart为0，colEnd为矩阵的列数减1。

然后，按照顺时针螺旋顺序遍历矩阵：

1. 从左到右遍历当前行的元素，并将它们添加到结果列表中。
2. 将rowStart加1，进入下一行。
3. 从上到下遍历当前列的元素，并将它们添加到结果列表中。
4. 将colEnd减1，进入下一列。
5. 如果rowStart仍然小于等于rowEnd，则从右到左遍历当前行的元素，并将它们添加到结果列表中。
6. 将rowEnd减1，进入上一行。
7. 如果colStart仍然小于等于colEnd，则从下到上遍历当前列的元素，并将它们添加到结果列表中。
8. 将colStart加1，进入下一列。
9. 重复步骤1~8，直到遍历完所有的元素。
10. 最后，返回结果列表。

通过以上的思路和算法，我们可以按照顺时针螺旋顺序遍历矩阵，并将元素添加到结果列表中。

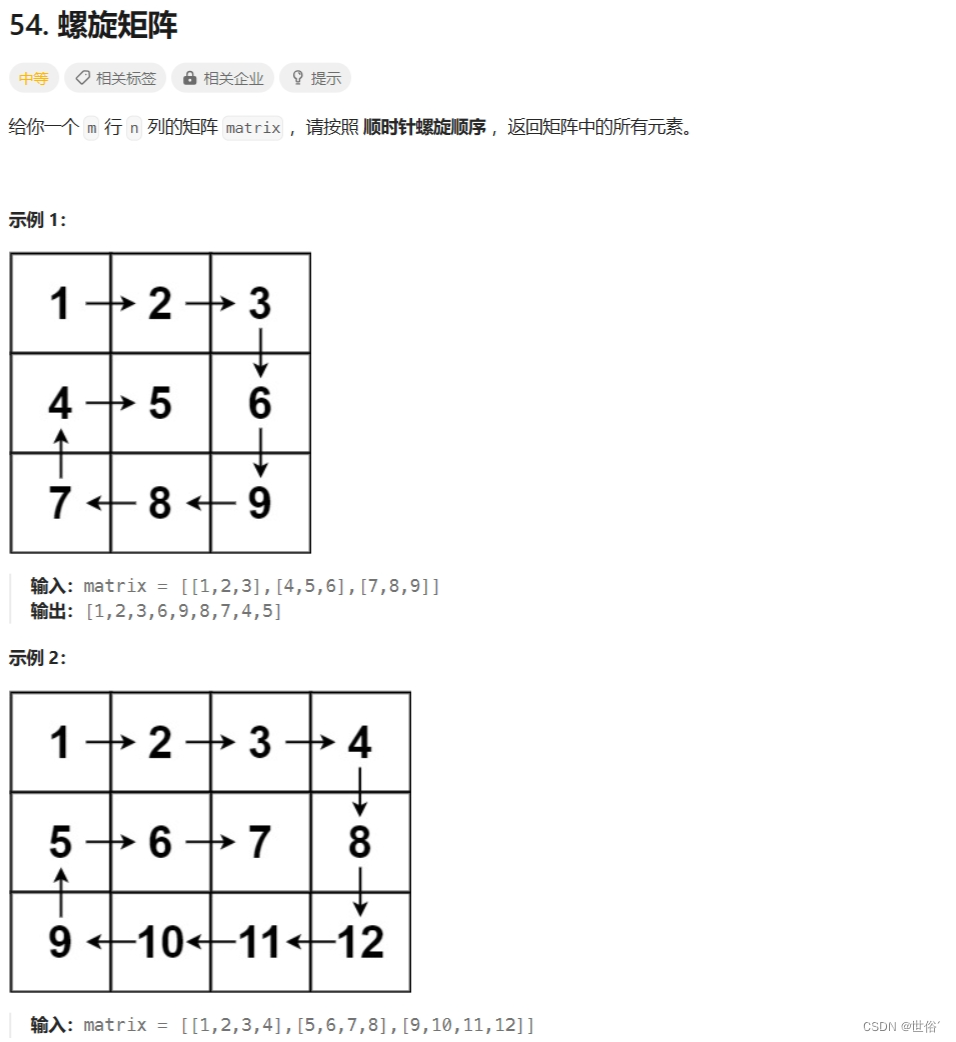
class Solution {public static List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0) {return result;}int rowStart = 0, rowEnd = matrix.length - 1;int colStart = 0, colEnd = matrix[0].length - 1;while (rowStart <= rowEnd && colStart <= colEnd) {// Traverse rightfor (int i = colStart; i <= colEnd; i++) {result.add(matrix[rowStart][i]);}rowStart++;// Traverse downfor (int i = rowStart; i <= rowEnd; i++) {result.add(matrix[i][colEnd]);}colEnd--;// Traverse leftif (rowStart <= rowEnd) {for (int i = colEnd; i >= colStart; i--) {result.add(matrix[rowEnd][i]);}rowEnd--;}// Traverse upif (colStart <= colEnd) {for (int i = rowEnd; i >= rowStart; i--) {result.add(matrix[i][colStart]);}colStart++;}}return result;}}

复杂度分析：

设矩阵的行数为m，列数为n。

• 时间复杂度：遍历矩阵中的每个元素需要O(m*n)的时间复杂度。
• 空间复杂度：除了存储结果的列表外，我们并没有使用额外的空间，因此空间复杂度为O(1)。

综上所述，该算法的时间复杂度为O(m*n)，空间复杂度为O(1)。

LeetCode运行结果：

方法二：递归

除了模拟遍历的方法，还可以使用递归解决螺旋矩阵问题。

该方法通过递归地遍历螺旋路径，在每一层递归中处理当前子矩阵的四条边。递归函数spiralOrderHelper接受子矩阵的边界索引和结果列表，然后按照顺时针螺旋顺序遍历矩阵并将元素添加到结果列表中。

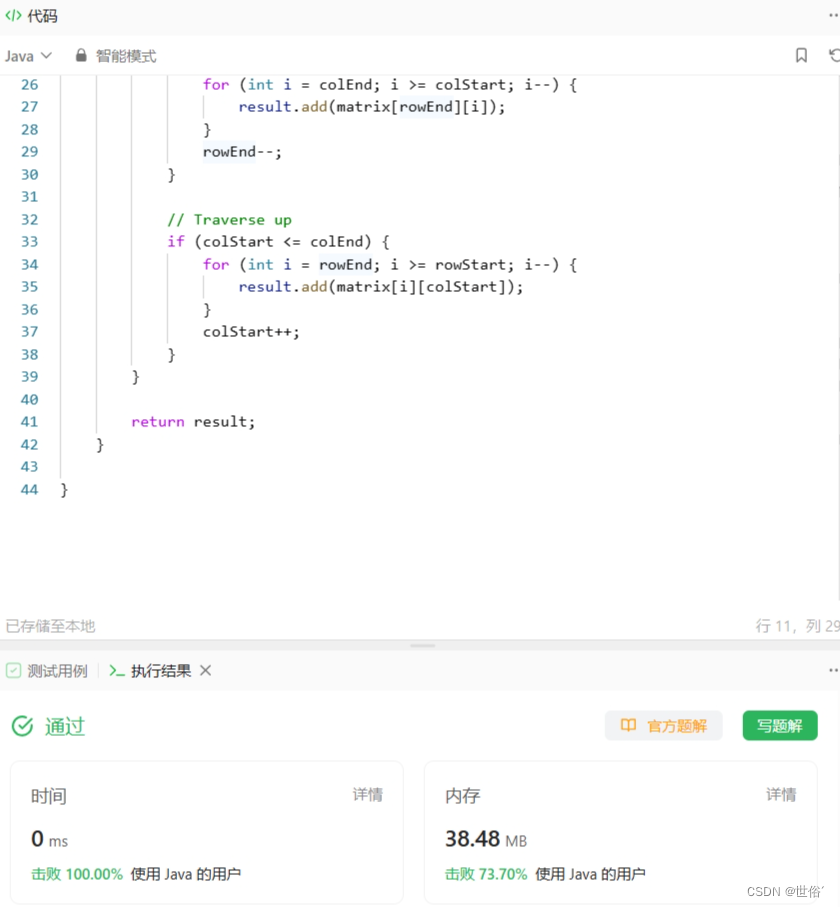
class Solution {public static List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0) {return result;}int m = matrix.length;int n = matrix[0].length;spiralOrderHelper(matrix, 0, m - 1, 0, n - 1, result);return result;}private static void spiralOrderHelper(int[][] matrix, int rowStart, int rowEnd, int colStart, int colEnd, List<Integer> result) {if (rowStart > rowEnd || colStart > colEnd) {return;}// Traverse rightfor (int i = colStart; i <= colEnd; i++) {result.add(matrix[rowStart][i]);}// Traverse downfor (int i = rowStart + 1; i <= rowEnd; i++) {result.add(matrix[i][colEnd]);}// Traverse leftif (rowStart < rowEnd) {for (int i = colEnd - 1; i >= colStart; i--) {result.add(matrix[rowEnd][i]);}}// Traverse upif (colStart < colEnd) {for (int i = rowEnd - 1; i > rowStart; i--) {result.add(matrix[i][colStart]);}}spiralOrderHelper(matrix, rowStart + 1, rowEnd - 1, colStart + 1, colEnd - 1, result);}
}

复杂度分析：

假设矩阵的大小是m × n（行数为m，列数为n），我们来分析一下递归解法的时间复杂度和空间复杂度。

时间复杂度分析： 递归函数的时间复杂度主要取决于两个因素：

• 每一层递归的时间复杂度：在每一层递归中，需要遍历边界上的元素，这个操作的时间复杂度是O(n+m)。因为每个元素需要访问一次，且没有重复访问。
• 递归的层数：递归的层数取决于矩阵的大小，即m和n的较小值。这是因为每一次递归都会缩小矩阵的规模，直到最后只剩下一个元素或者没有元素。

所以，递归解法的总的时间复杂度可以表示为O((n+m) * min(m, n))，其中n和m分别表示矩阵的列数和行数。

空间复杂度分析： 递归函数的空间复杂度主要取决于两个因素：

• 递归调用栈的大小：每一层递归都会在调用栈中占用一定的空间，具体的大小取决于递归的层数。由上面分析可知，递归的层数是O(min(m, n))。
• 存储结果的空间：递归函数需要返回一个螺旋遍历的结果，这个结果列表的大小与矩阵中的元素个数相同，即m * n。

因此，递归解法的总的空间复杂度可以表示为O(m * n + min(m, n))。

综上所述，使用递归解决螺旋矩阵问题的时间复杂度是 O((n+m) * min(m, n))，空间复杂度是 O(m * n + min(m, n))。在矩阵较大时，递归解法可能会造成栈溢出或者额外的空间开销较大，因此在实际应用中需要谨慎使用。

LeetCode运行结果：

方法三：方向转换法

这种方法基于对螺旋矩阵的特性进行分析，通过不断改变遍历方向来遍历整个矩阵。具体步骤如下：

1. 定义4个边界：上边界、下边界、左边界、右边界。
2. 初始化当前位置为(0, 0)，遍历方向为向右。
3. 当遍历方向向右时，先向右遍历直到到达右边界，然后将上边界下移一行，遍历方向转为向下。
4. 当遍历方向向下时，先向下遍历直到到达下边界，然后将右边界左移一列，遍历方向转为向左。
5. 当遍历方向向左时，先向左遍历直到到达左边界，然后将下边界上移一行，遍历方向转为向上。
6. 当遍历方向向上时，先向上遍历直到到达上边界，然后将左边界右移一列，遍历方向转为向右。
7. 重复上述步骤，直到遍历完整个矩阵。

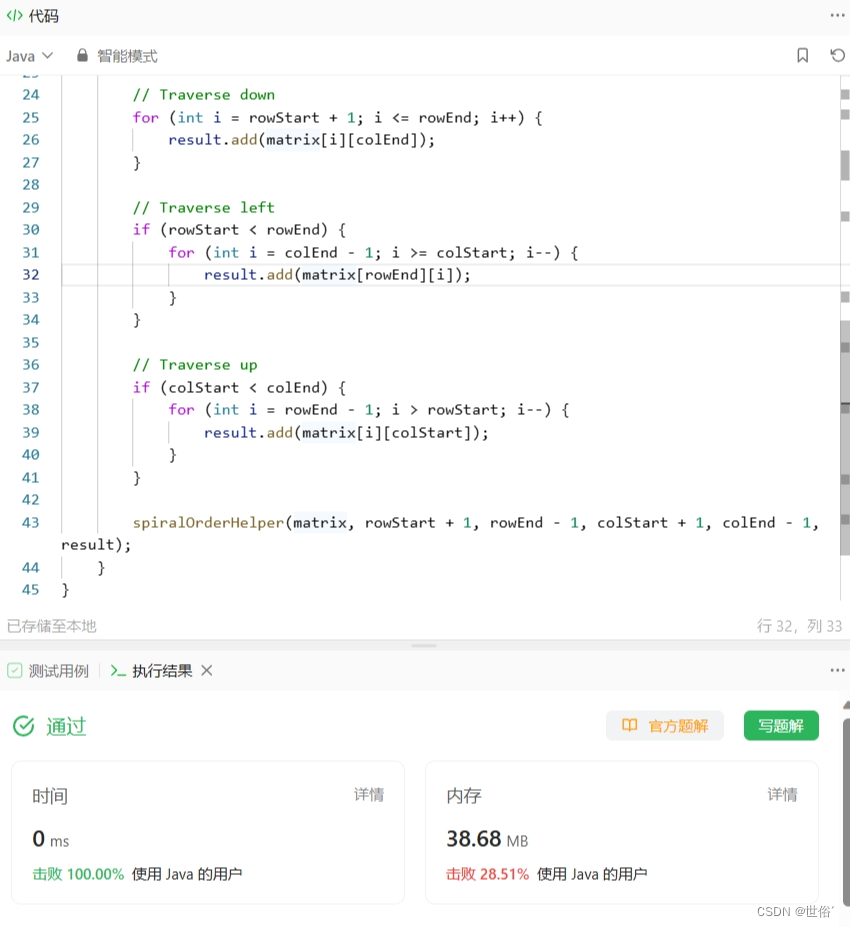
class Solution {public static List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return result;}int m = matrix.length; // 行数int n = matrix[0].length; // 列数int top = 0, bottom = m - 1, left = 0, right = n - 1;int direction = 0; // 0表示向右, 1表示向下, 2表示向左, 3表示向上while (top <= bottom && left <= right) {if (direction == 0) { // 向右遍历for (int i = left; i <= right; i++) {result.add(matrix[top][i]);}top++; // 上边界下移一行} else if (direction == 1) { // 向下遍历for (int i = top; i <= bottom; i++) {result.add(matrix[i][right]);}right--; // 右边界左移一列} else if (direction == 2) { // 向左遍历for (int i = right; i >= left; i--) {result.add(matrix[bottom][i]);}bottom--; // 下边界上移一行} else if (direction == 3) { // 向上遍历for (int i = bottom; i >= top; i--) {result.add(matrix[i][left]);}left++; // 左边界右移一列}direction = (direction + 1) % 4; // 改变遍历方向}return result;}
}

复杂度分析：

这种方法只需要遍历一次矩阵，时间复杂度为O(m * n)，空间复杂度为O(1)。

LeetCode运行结果：

方法四：螺旋填数法

这种方法实际上是构造螺旋矩阵的过程，可以直接得到螺旋遍历的结果。具体步骤如下：

1. 定义4个边界：上边界、下边界、左边界、右边界。
2. 初始化当前数字为1，遍历方向为向右。
3. 当遍历方向向右时，从左到右填充当前行的所有元素，并将上边界下移一行。
4. 当遍历方向向下时，从上到下填充当前列的所有元素，并将右边界左移一列。
5. 当遍历方向向左时，从右到左填充当前行的所有元素，并将下边界上移一行。
6. 当遍历方向向上时，从下到上填充当前列的所有元素，并将左边界右移一列。
7. 重复上述步骤，直到填充完整个矩阵。

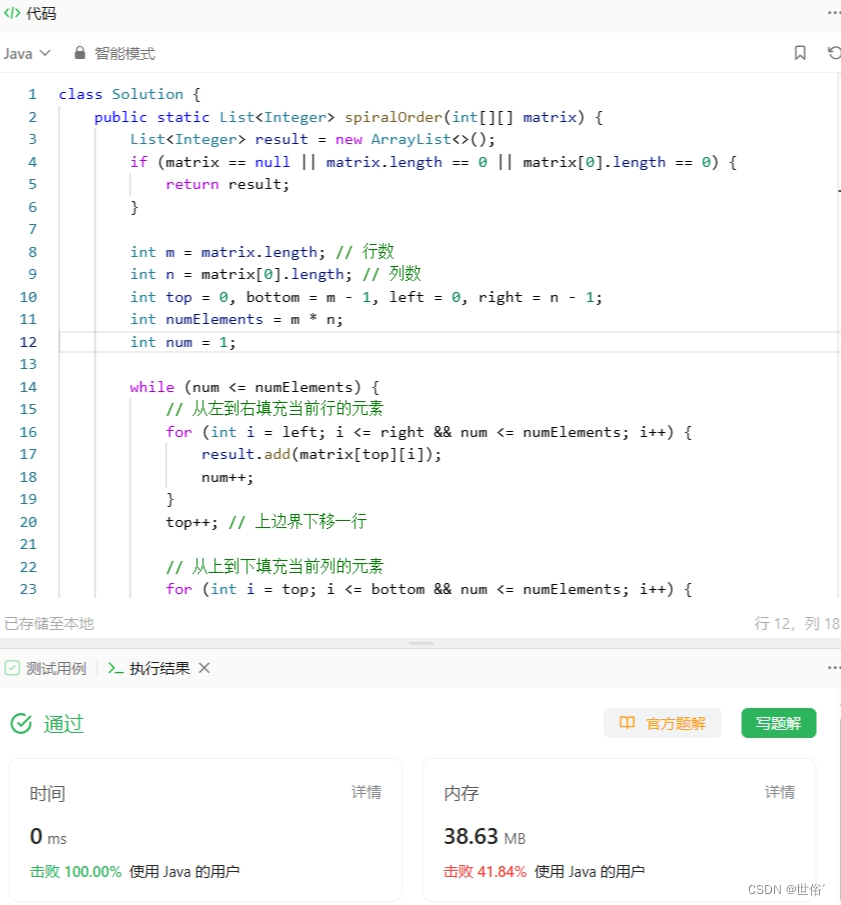
class Solution {public static List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return result;}int m = matrix.length; // 行数int n = matrix[0].length; // 列数int top = 0, bottom = m - 1, left = 0, right = n - 1;int numElements = m * n;int num = 1;while (num <= numElements) {// 从左到右填充当前行的元素for (int i = left; i <= right && num <= numElements; i++) {result.add(matrix[top][i]);num++;}top++; // 上边界下移一行// 从上到下填充当前列的元素for (int i = top; i <= bottom && num <= numElements; i++) {result.add(matrix[i][right]);num++;}right--; // 右边界左移一列// 从右到左填充当前行的元素for (int i = right; i >= left && num <= numElements; i--) {result.add(matrix[bottom][i]);num++;}bottom--; // 下边界上移一行// 从下到上填充当前列的元素for (int i = bottom; i >= top && num <= numElements; i--) {result.add(matrix[i][left]);num++;}left++; // 左边界右移一列}return result;}
}

复杂度分析：

这种方法也只需要遍历一次矩阵，时间复杂度为O(m * n)，空间复杂度为O(1)。

LeetCode运行结果：