【二叉树练习题】

在这里插入图片描述

欢迎来到我的：世界

希望作者的文章对你有所帮助，有不足的地方还请指正，大家一起学习交流 !

前言

本篇文章共有9道题，其中4题是初阶，5题是进阶题；希望该文章对你有帮助！

初阶题

既然了解的二叉树的基本结构，接下来了解几个有关二叉树的基本函数吧！

二叉树的节点个数

如果知道一颗二叉树，那怎么求这颗二叉树的节点个数呢？

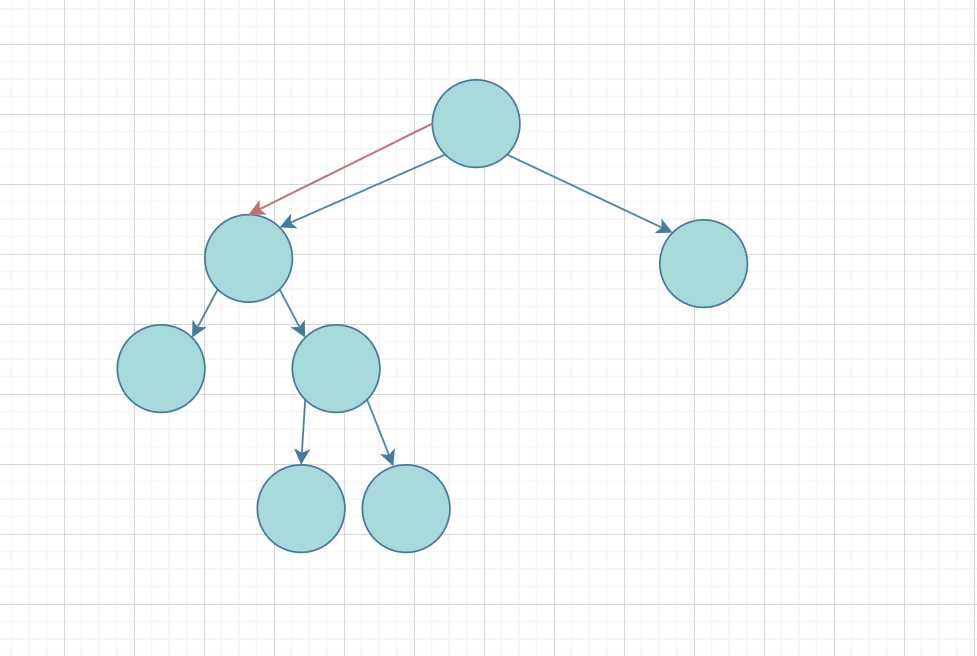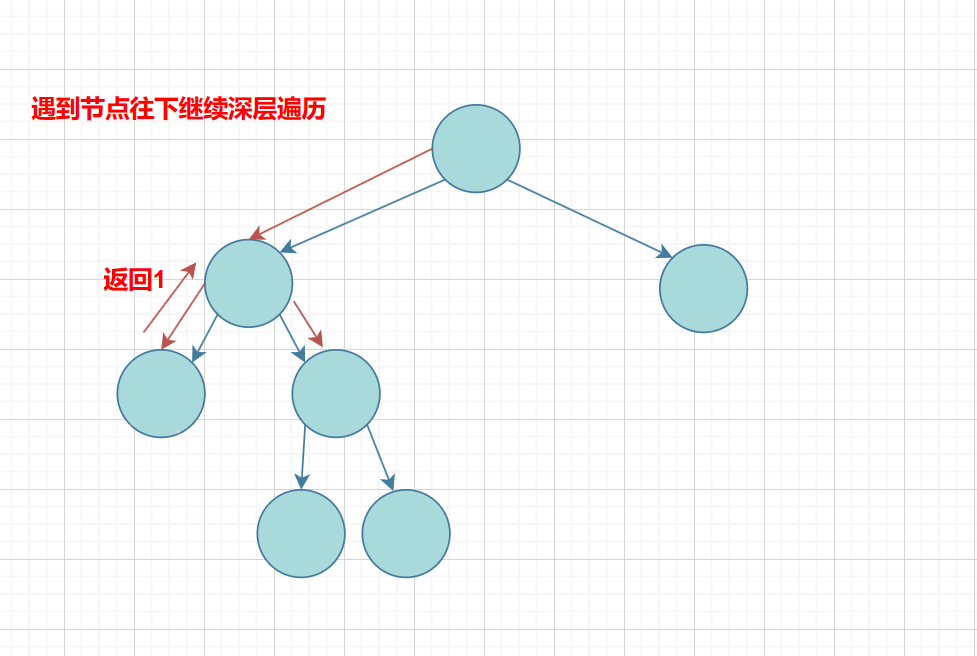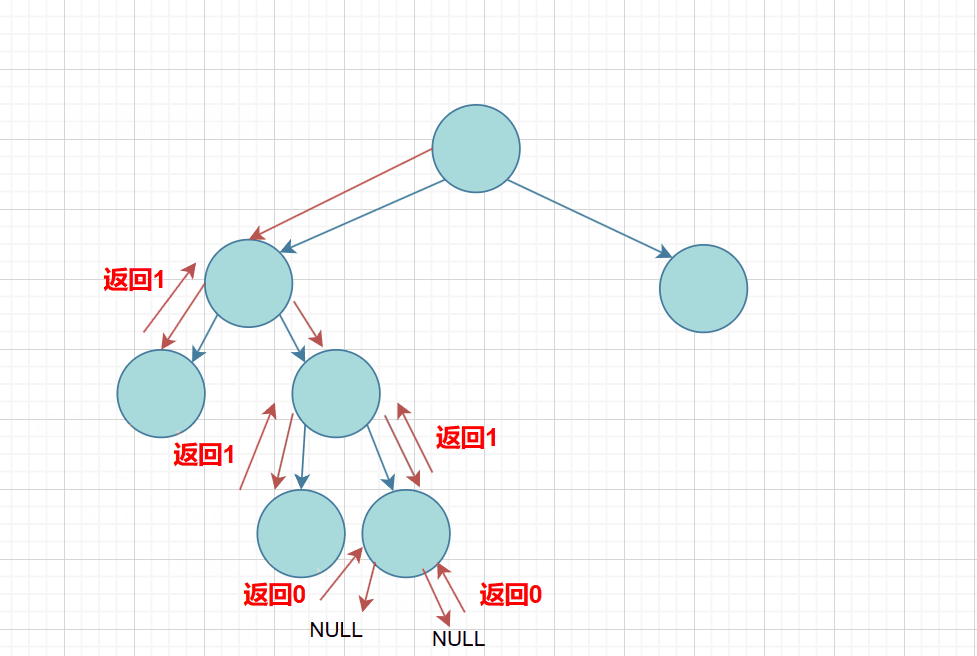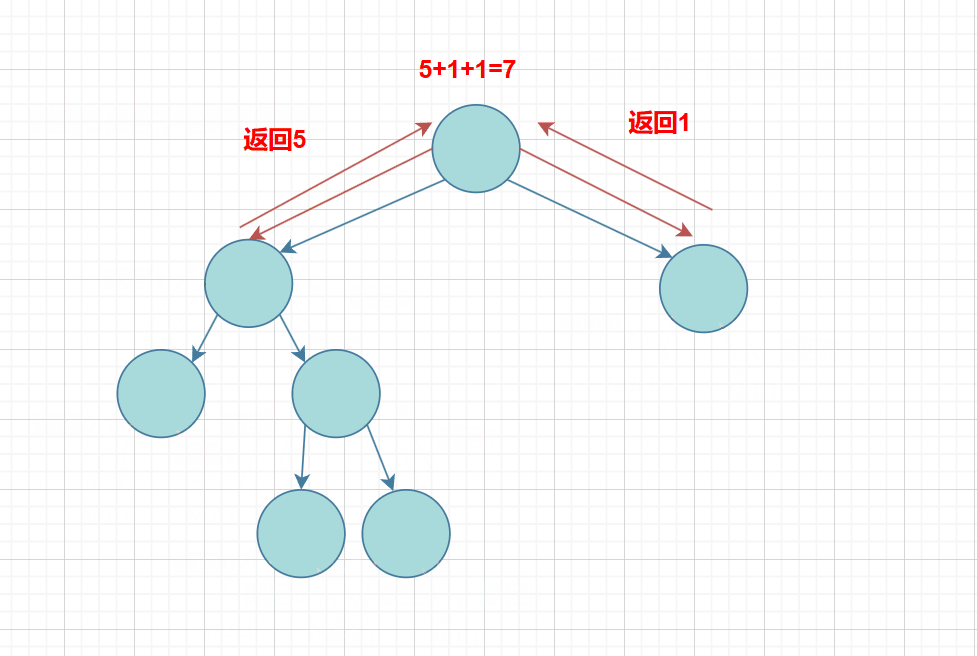
思路： 我们可以利用树的递归的思想，遍历这颗树，这里我们用前序遍历：如果遇到节点就再向左右子树深层递归下去+1(其本身)，直到遇到空就返回0；
下面根据图解的方式：

代码实现：

//二叉树的节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

二叉树的叶子节点个数

知道二叉树的节点个数，那叶子结点个数呢？
叶子节点是和普通的节点不一样的，叶子结点其特点是：没有子节点的，所以我们可以根据这一特性来解决这个问题；

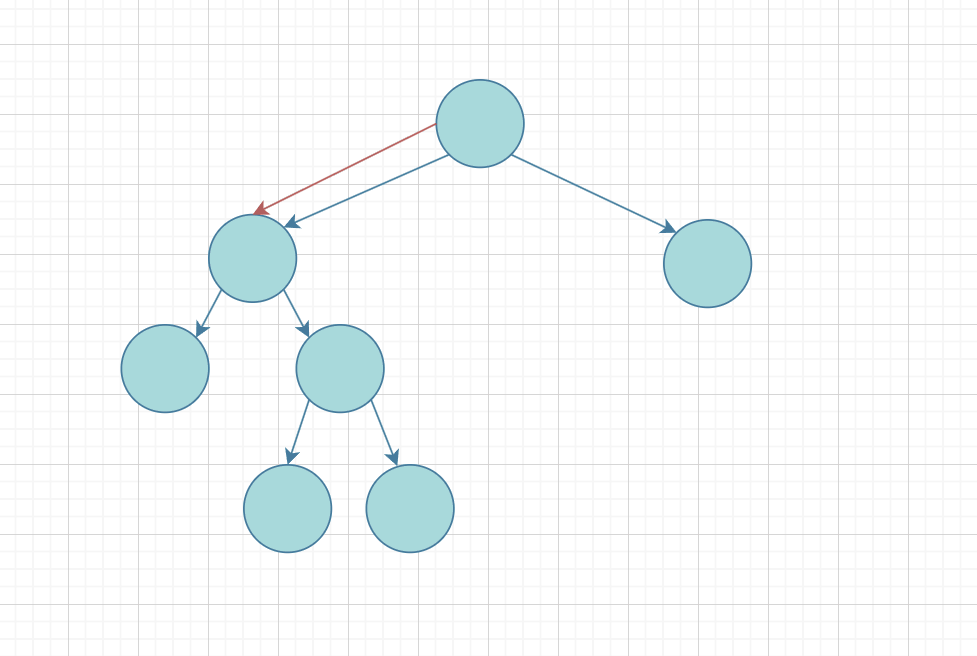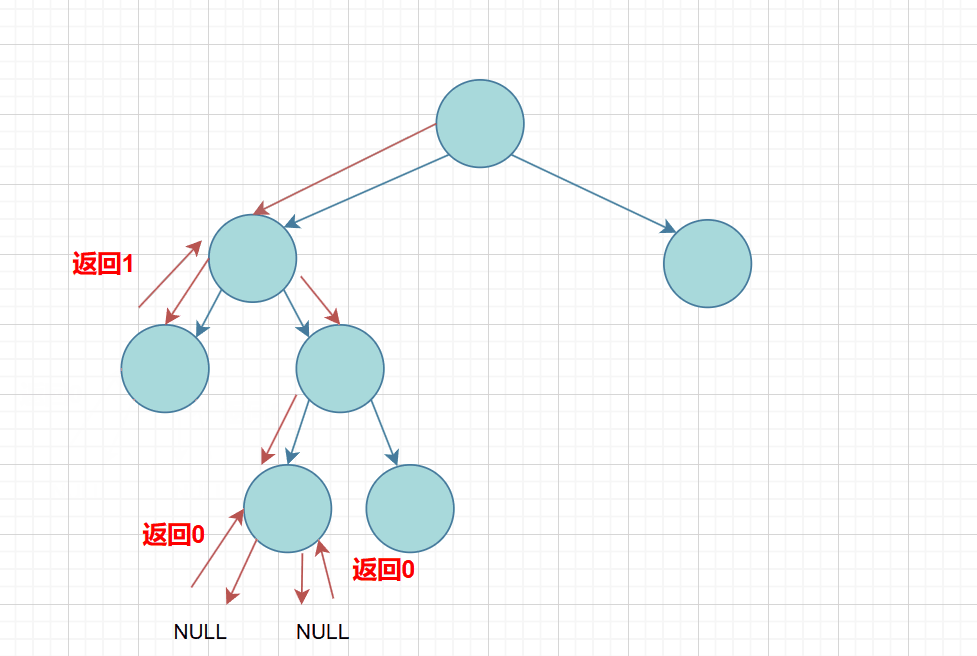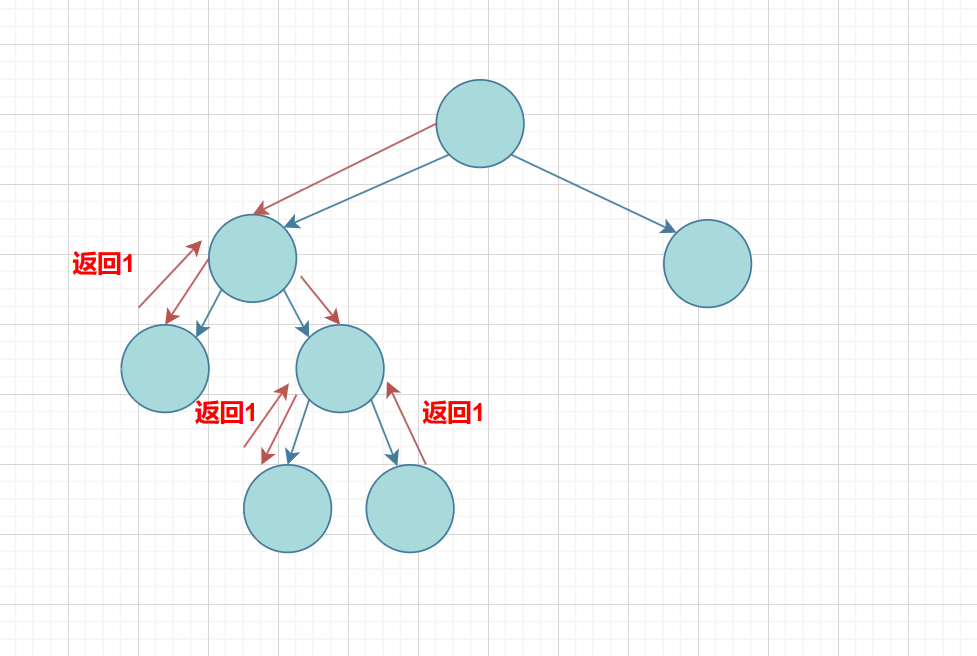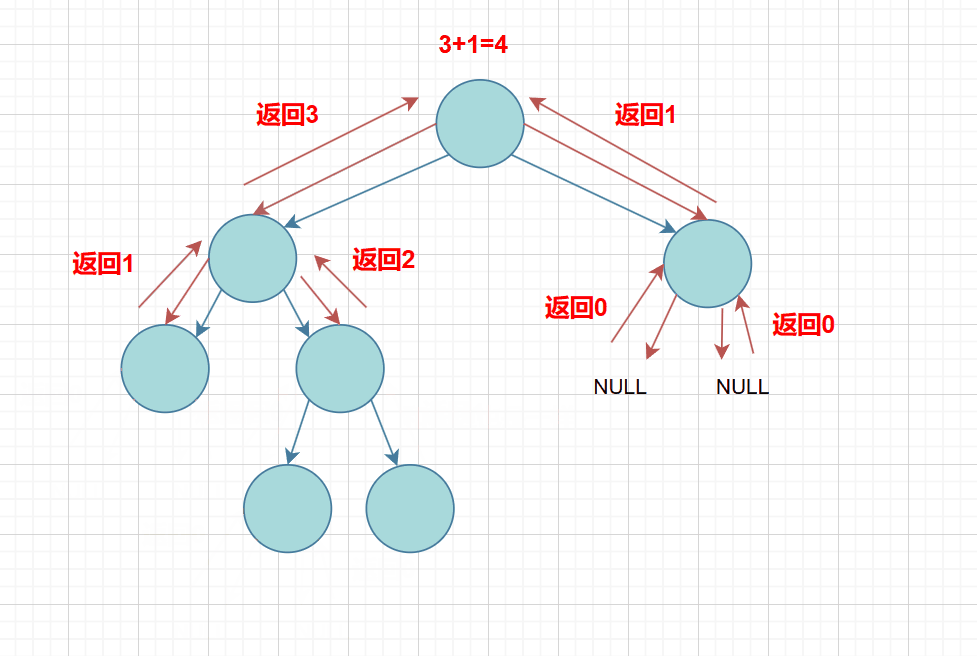
思路：我们还是可以利用二叉树树的结构特点，前序遍历这颗二叉树树，如果节点的左右节点返回=0，那就说明该节点是叶子结点，那就返回1，否则就返回左右子树的值；

代码实现：

//求叶子节点的个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;int left = BinaryTreeLeafSize(root->left);int right = BinaryTreeLeafSize(root->right);return left + right == 0 ? 1 : (left + right);
}

注意：关于这代码实现，可能有老铁想过可以这样写代码是不是方便点：
代码：错误的示例

//求叶子节点的个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right) == 0  ? 1 : (BinaryTreeLeafSize(root->left) +  BinaryTreeLeafSize(root->right));
}

这样想的话就是理解的不够深刻，你要知道每次递归调用这个函数，调用的栈空间就越大，栈的空间不大，调用的越深越容易栈溢出；还有一点，你要知道的是这个节点的左右子树的返回值，如在前面的已经知道该节点的左右子树的返回值和，在往后走就会再一次往深层遍历一次了，这完全是没有必要，多此一举；

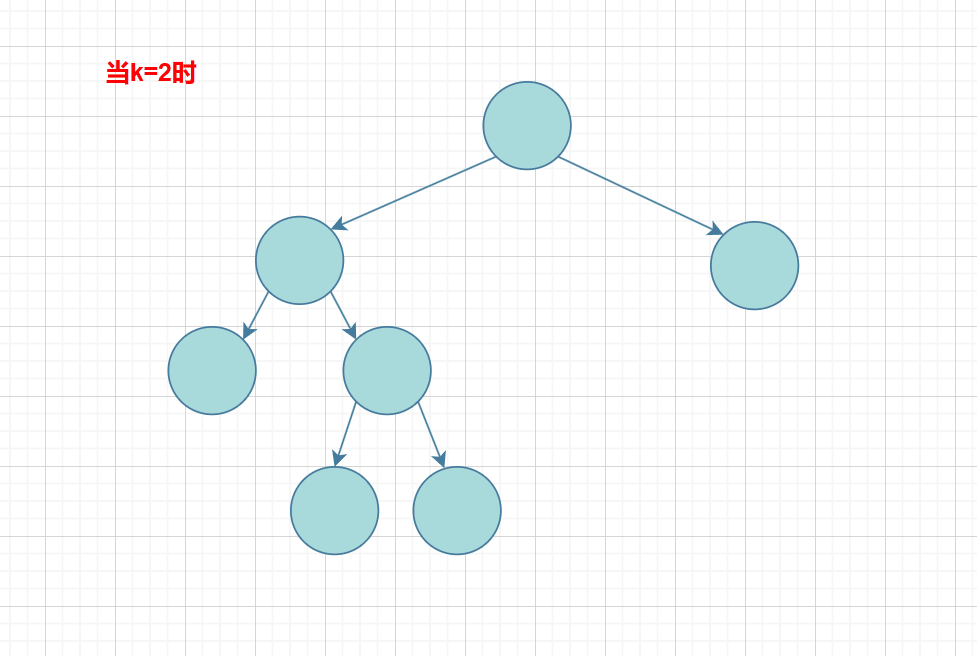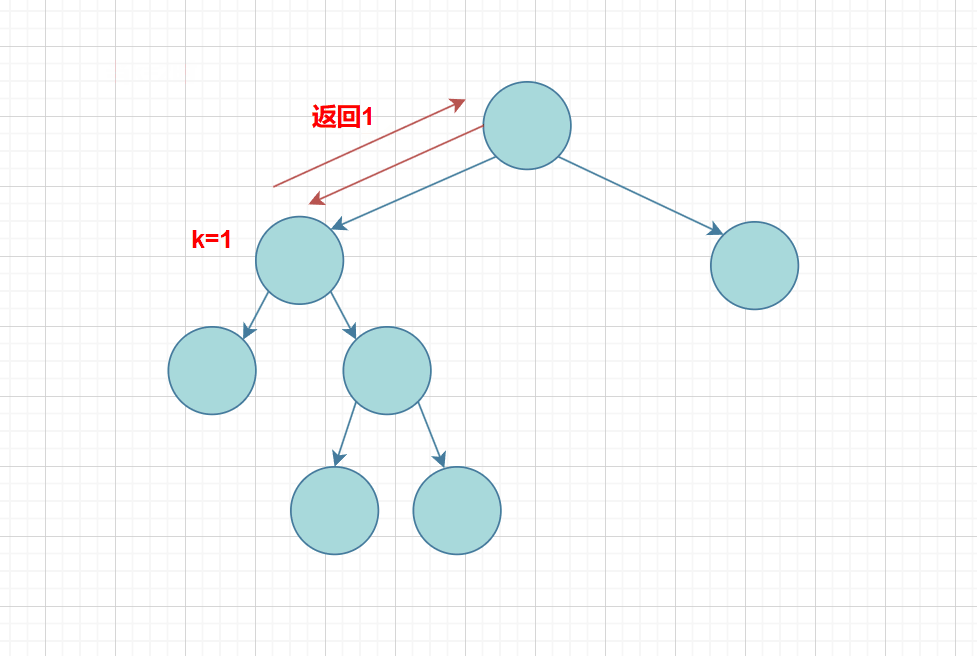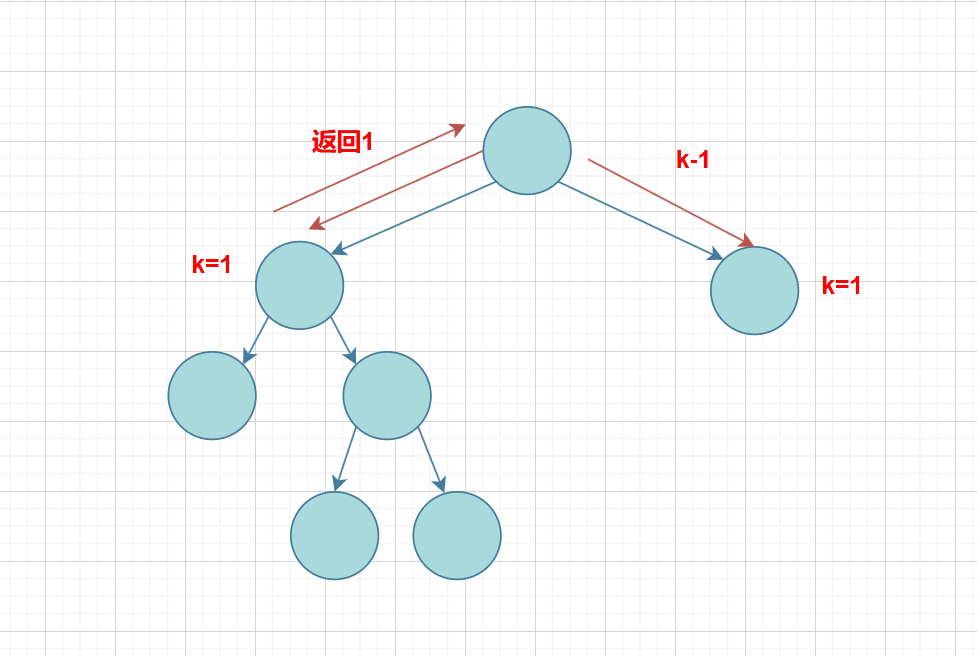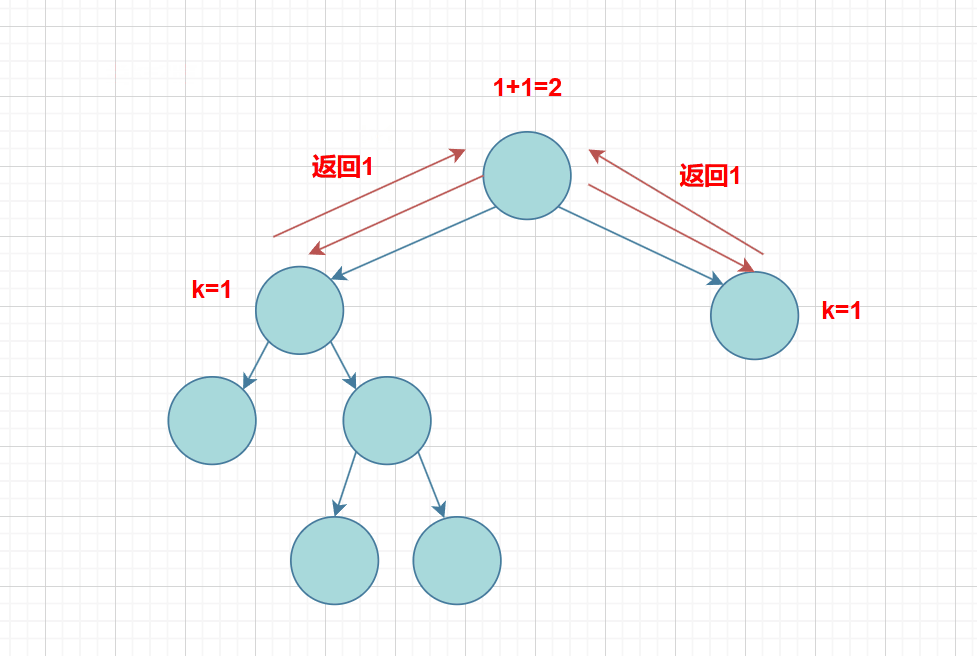
二叉树第k层节点个数

下面来加一点点难度吧！

思路:就是关键的k的值，在每次递归调用的时候 k-1，就可以实现了，不过还要加一条条件：如果当k==1时，就到了要求k层的节点个数的那层，这时只要不为空，则都返回 1，记住：这是求第k层的节点个数；

代码实现：

//二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1 )return 1;return BinaryTreeLevelKSize(root->left, k-1) + BinaryTreeLevelKSize(root->right, k-1);
}

二叉树查找值为x的节点

思路：二叉树最常利用的递归的思想，往下遍历一遍，找到了一样的值，就返回该值的结点，否则就返回NULL；
代码实现：

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->val == x)return root;BTNode* left = BinaryTreeFind(root->left, x);if (left)return left;BTNode* right = BinaryTreeFind(root->right, x);if (right)return right;
}

有一个改善版本：

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->val == x)return root;BTNode*left=BinaryTreeFind(root->left,x);if (left)return left;return BinaryTreeFind(root->right,x);
}

进阶题

完全二叉树的节点个数

地址：oj地址

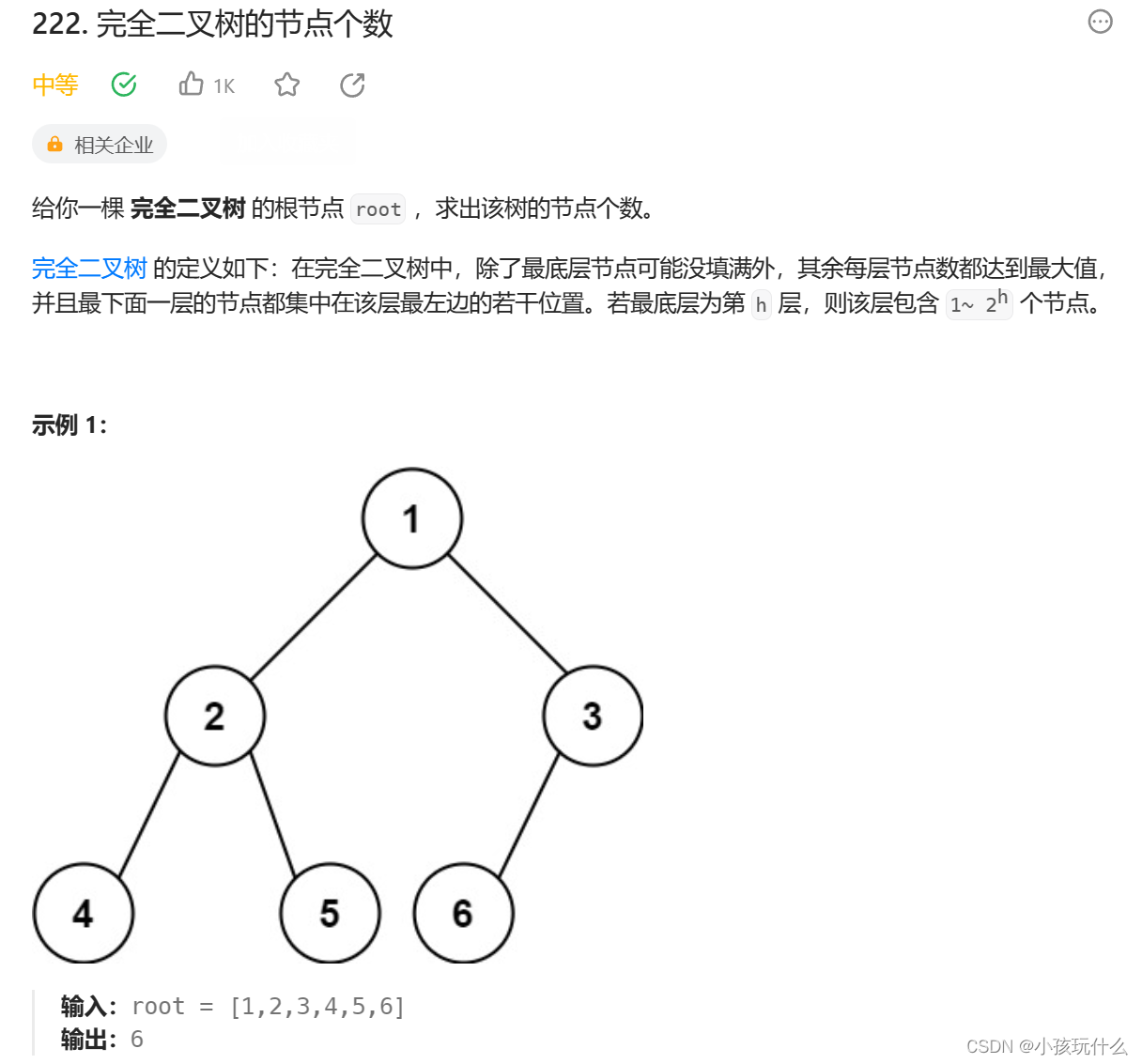
在这里插入图片描述

解题思路：

这道题仔细一看是不是和我们上面初阶那道：求二叉树的节点个数一样，那这题是完全二叉树的结点个数，那不是肯定能行么？那我们先试一试能不能过；
答案是：过了；

代码实现：

//完全二叉树的节点个数
int countNodes(struct TreeNode* root){
return root == NULL ? 0 : countNodes(root->left) + countNodes(root->right) + 1;
}

翻转二叉树

地址：oj地址

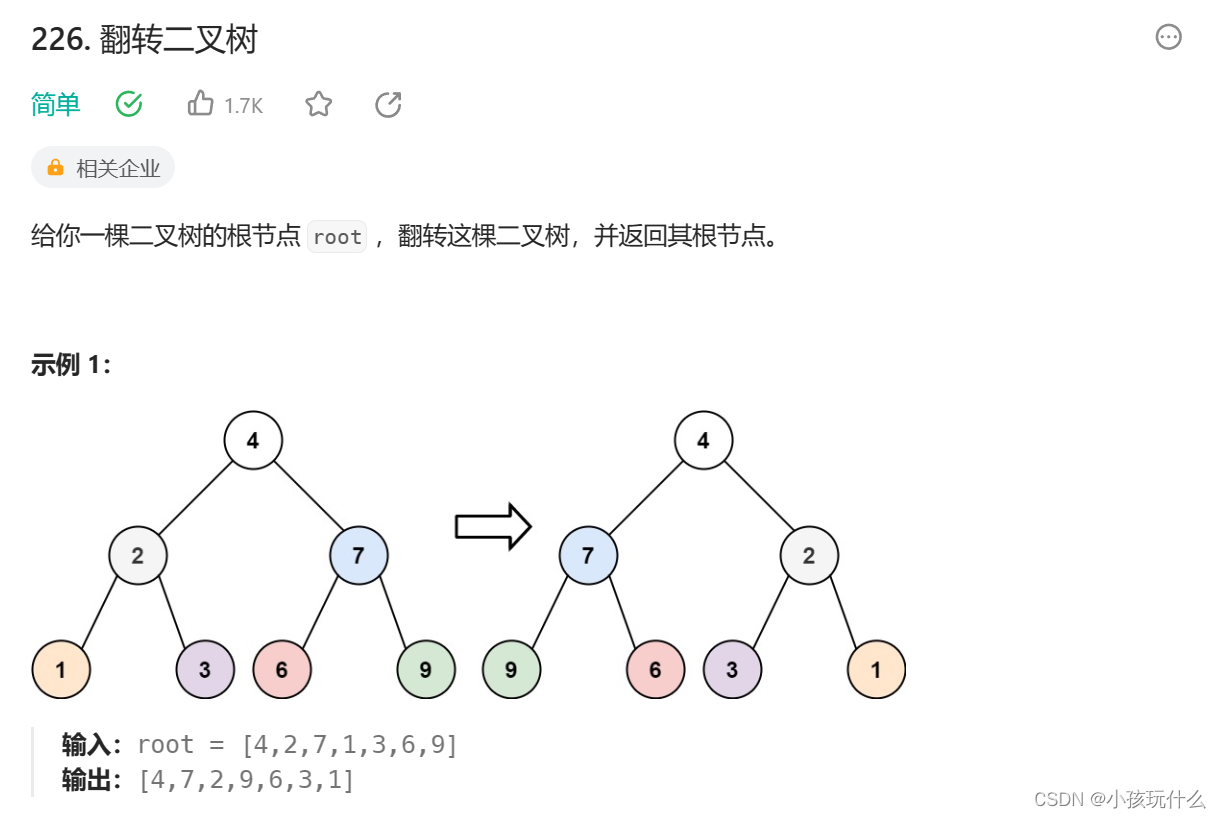
在这里插入图片描述

解题思路：
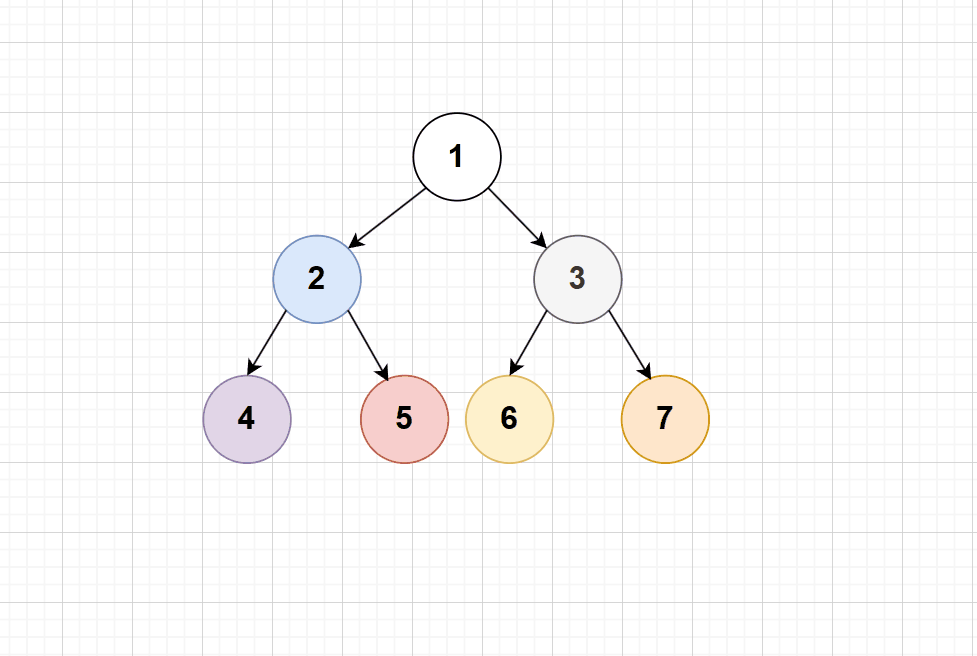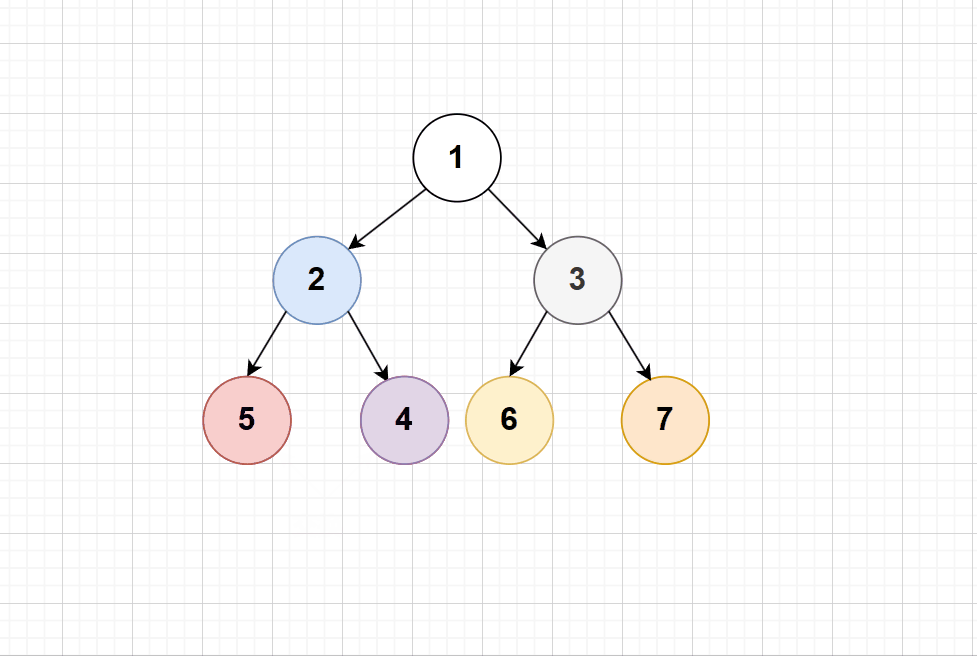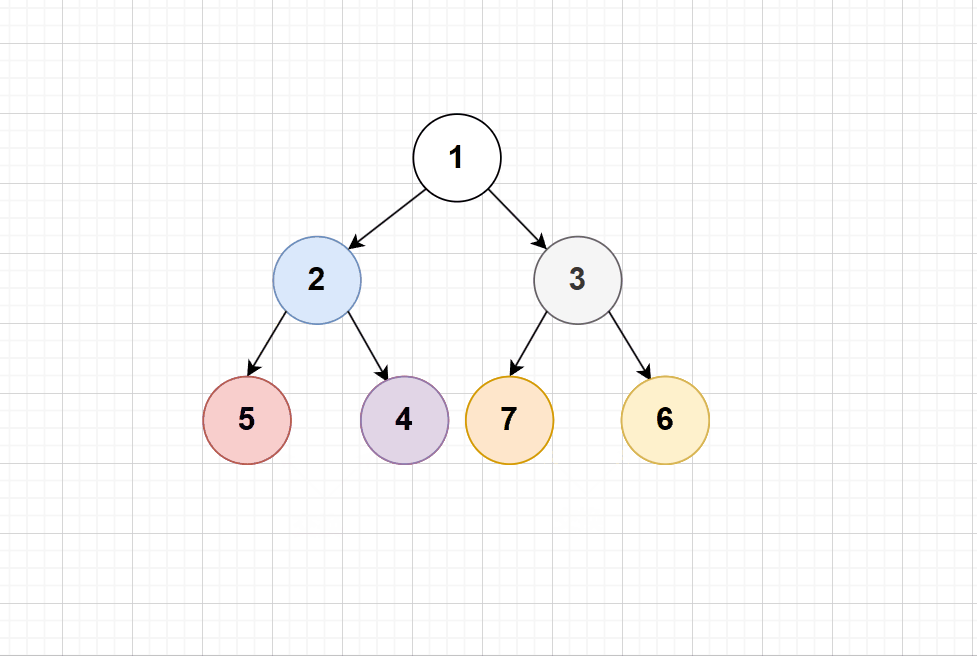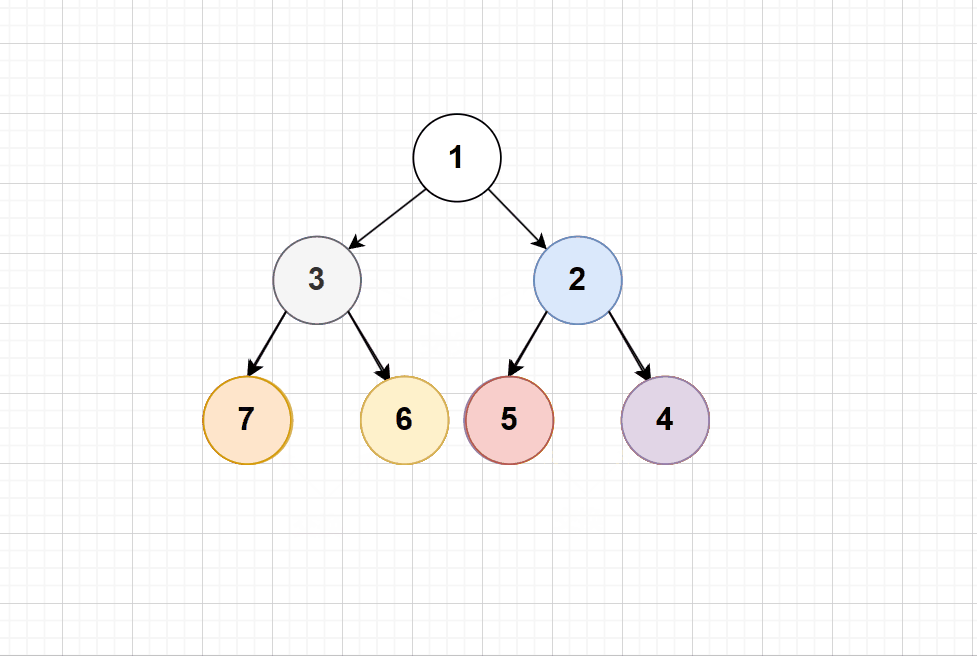
可以看出，交换节点的左右子树即可；需要注意的是：返回的是节点本身，这要才能连带着其子节点交换过去；

//翻转二叉树
struct TreeNode* invertTree(struct TreeNode* root){if(root==NULL)return NULL;struct TreeNode*left=invertTree(root->left);struct TreeNode*right=invertTree(root->right);root->left=right;root->right=left;return root;
}

检验两个树是否相同

地址：oj地址

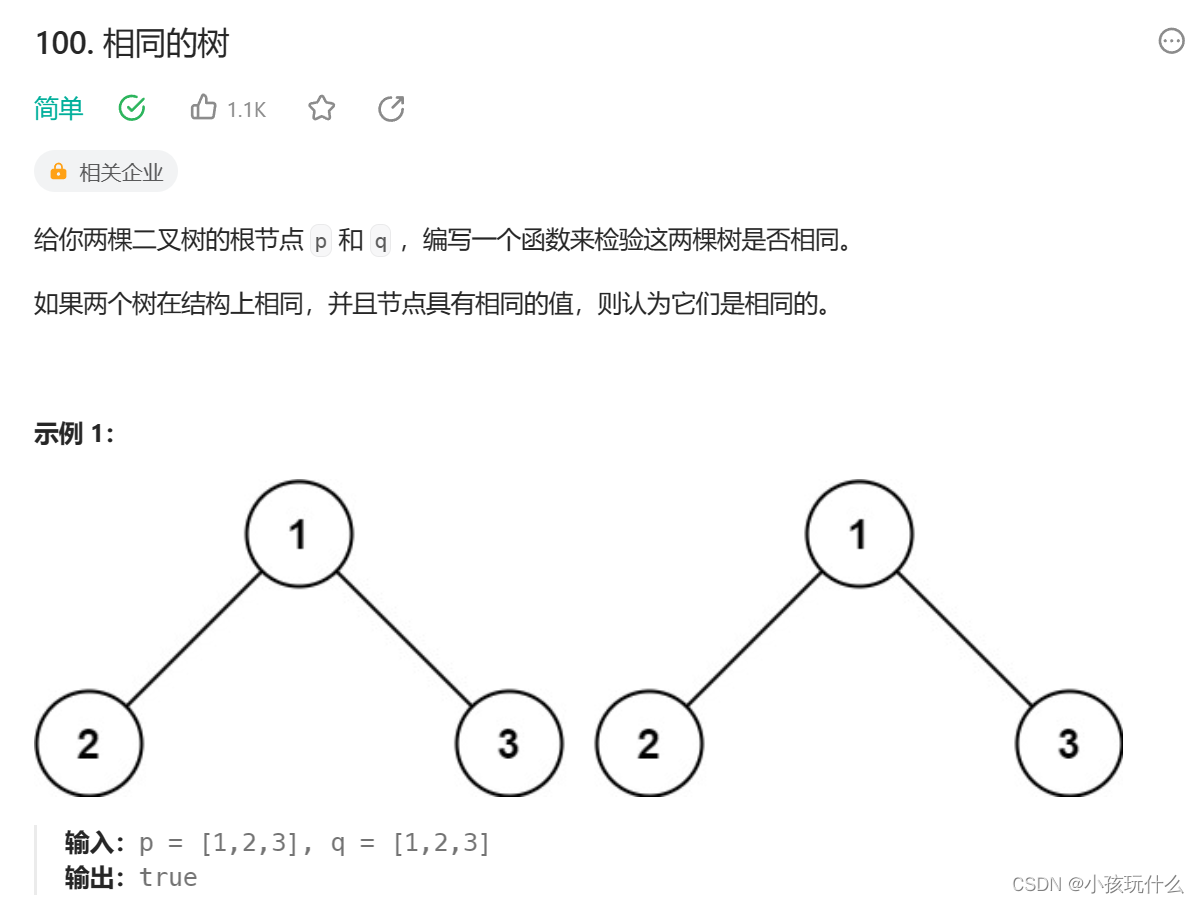
在这里插入图片描述

解题思路：
两颗树完全相同，代表着其所有子节点值都相同，那就同时遍历两颗树，是两颗树的左子树和左子树进行比较，右子树和右子树进行比较，绝不能左子树和右子树进行比较；遍历到底时，如果两树的节点都指向NULL则代表相同就返回true；如果只有其中一个节点指向NULL则代表两个节点不同返回flase，当两个节点指向的都不是NULL，那就比较节点值，不同的则返回flase；最后的判断条件，只要两颗树都返回true，则代表两颗树相同；

代码实现：

bool isSameTree(struct TreeNode* p, struct TreeNode* q){//两个都为空if(p==NULL && q==NULL)return true;//其中一个为空if(p==NULL || q==NULL)return false;if(p->val!=q->val)return false;return isSameTree(p->left,q->left) &&isSameTree(p->right,q->right);
}

对称二叉树

地址：oj地址

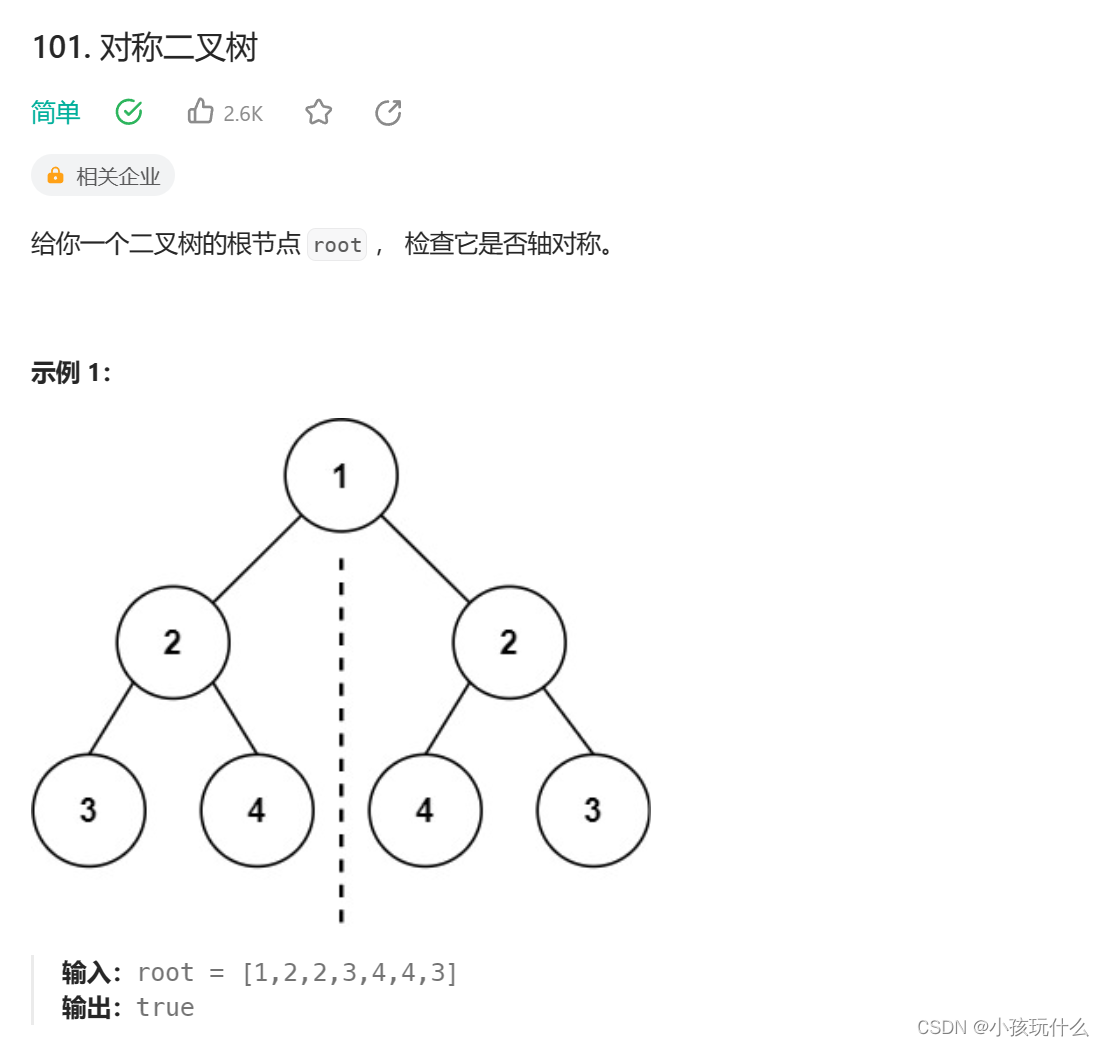
在这里插入图片描述

解题思路：
看一颗二叉树是否对称，完全可以以根节点当做是对称轴，然后比较根节点的左子树和右子树是否对称即可；简化为判断两棵树是否对称，这时候上面的一题：相同的树；很像，但不同的是对称，不是相同，所以我们需要变化一下，在相同的树的解题思路上，注意一点：他要比较的是一颗树的左子树和另一颗树的右子树进行比较，所以根据这点：

代码实现：

bool Cheak(struct TreeNode*q,struct TreeNode*p)
{//两个都为空if(p==NULL && q==NULL)return true;//其中一个为空if(p==NULL || q==NULL)return false;if(p->val!=q->val)return false;return Cheak(q->left,p->right) &&Cheak(q->right,p->left);
}bool isSymmetric(struct TreeNode* root){struct TreeNode*left =root->left;struct TreeNode*right=root->right;return Cheak(left,right);
}

检验是否是其子树

地址：oj地址

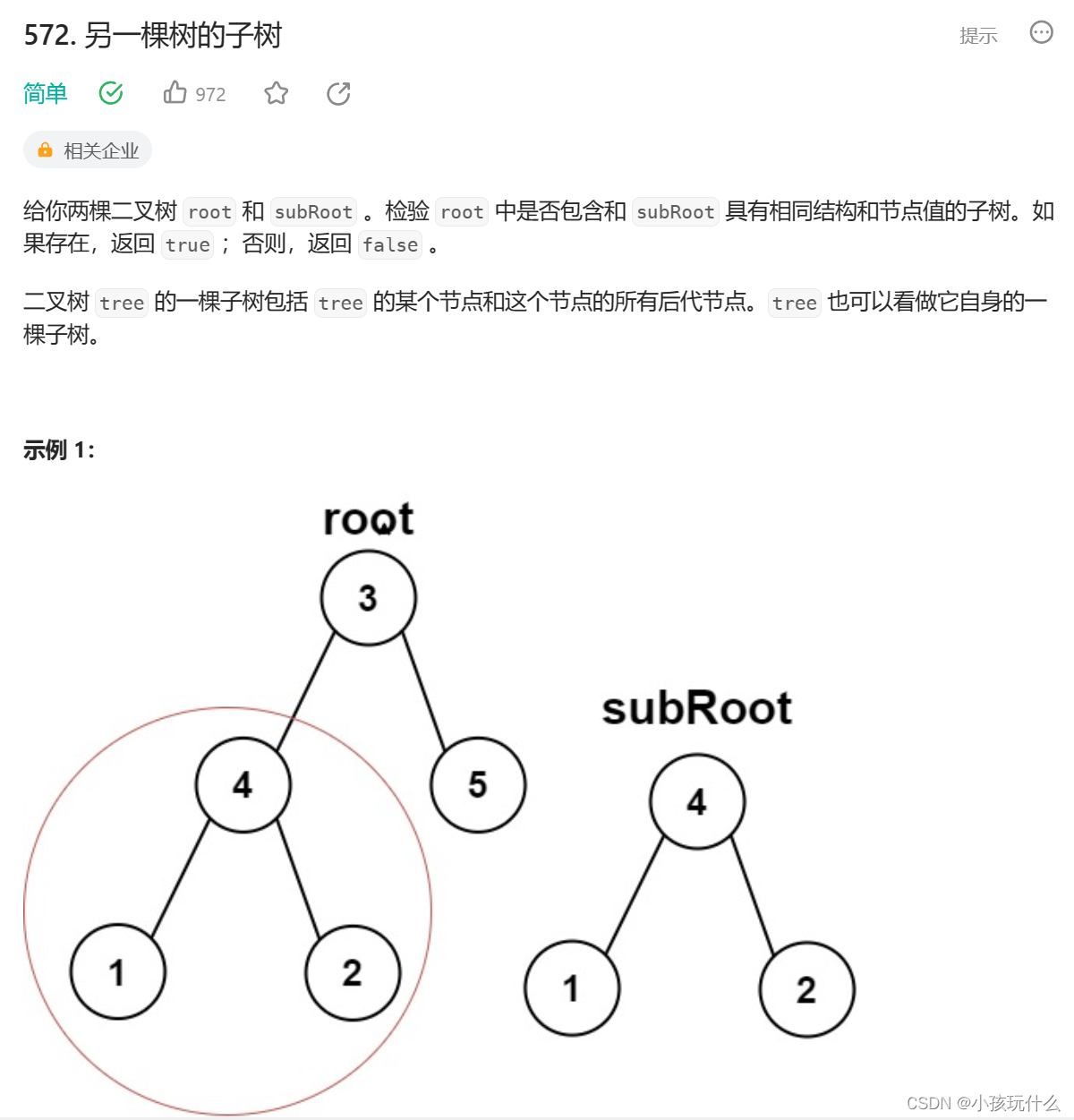
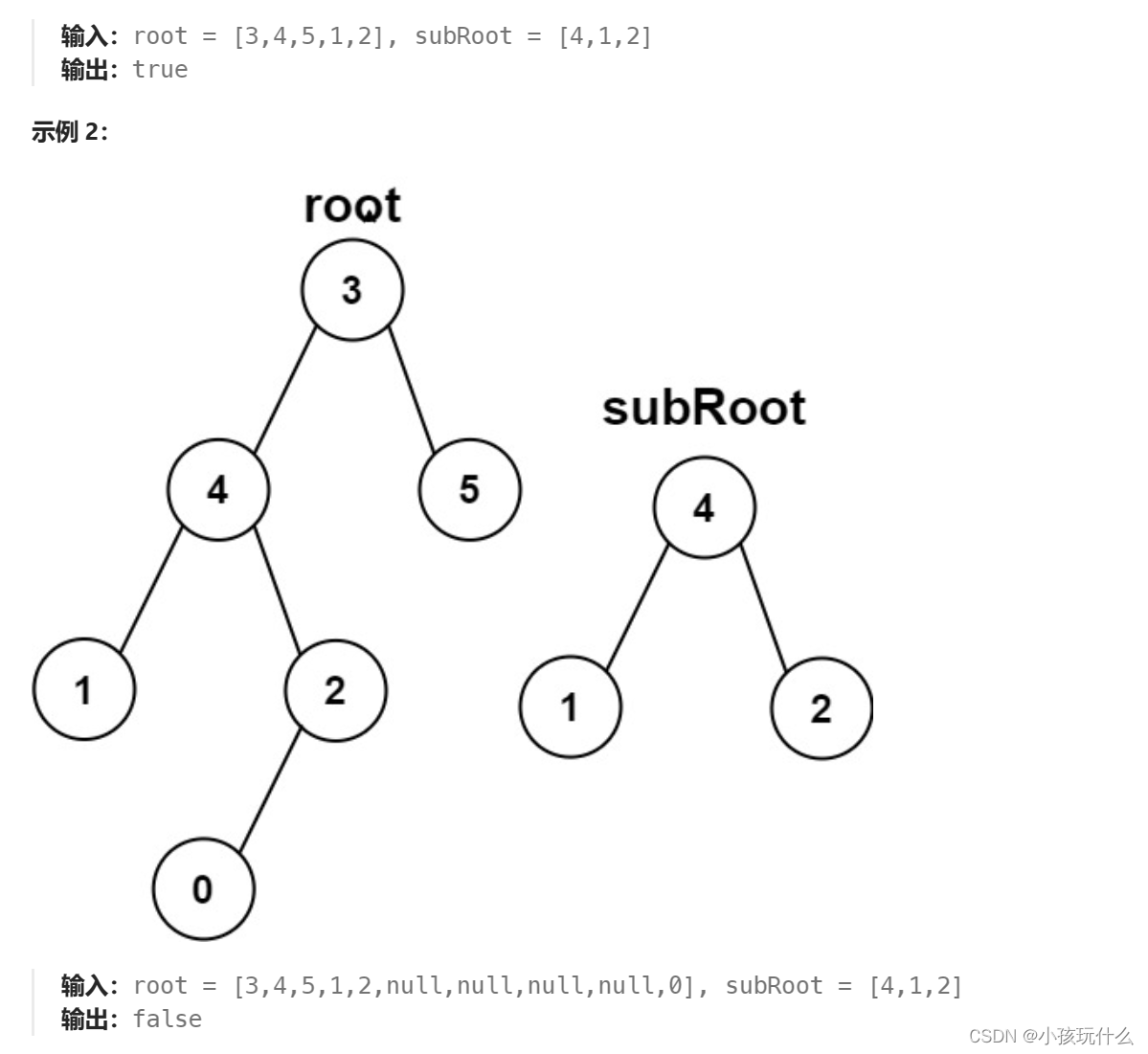
在这里插入图片描述

解题思路：
这题我们可以换个思路：找到root树中与subRoot树相同的根节点后，就比较这两颗树是否相同，如果都相同，则代表subRoot树是root树的子树；只要找到相同的树，就不需要再找了；

代码实现：

bool isSameTree(struct TreeNode* p, struct TreeNode* q){//两个都为空if(p==NULL && q==NULL)return true;//其中一个为空if(p==NULL || q==NULL)return false;if(p->val!=q->val)return false;return isSameTree(p->left,q->left) &&isSameTree(p->right,q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root==NULL)return false;if(root->val==subRoot->val){if(isSameTree(root,subRoot))return true;}return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}