目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
一、支持向量机(SVM)
二、多层感知器(MLP)
5.算法完整程序工程
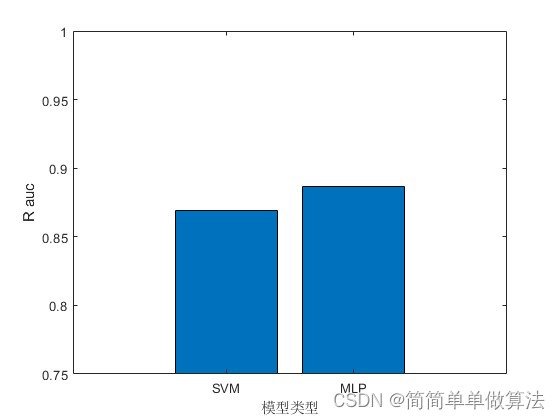
1.算法运行效果图预览






2.算法运行软件版本
matlab2022a
3.部分核心程序
...................................................................
%SVM
% 以下是关于SVM模型的设置。
% 并行计算设置,使用多核CPU进行计算。
svm_opt = statset('UseParallel',true);tic% 开始计时,计算模型训练时间。
% 使用fitcsvm函数训练SVM模型,其中标准化设为真,核函数、多项式阶数、盒子约束等参数进行设置。结果为最优的SVM模型svm_optimal。
svm_models = fitcsvm(xTrain,yTrain, 'Standardize', true,...'KernelFunction',"polynomial",...% "polynomial"核函数是一个多项式核函数,它对应于无穷维特征空间中的点积。 'PolynomialOrder' ,2,...% "2"定义了多项式的阶数'BoxConstraint',0.8);%"0.8"定义了约束条件。
% 计算并存储SVM模型训练时间。
Time_svm = toc;
% 对测试集进行预测和评价。
yr_svm = predict(svm_models, xTest);........................................................................
%MLP
% 以下是关于多层感知器(MLP)模型的设置。
% MLP的超参数
mlp_models.divideFcn = 'dividerand'; %将数据随机划分
mlp_models.divideMode = 'sample'; %对每个样本进行划分
mlp_models.divideParam.trainRatio = 0.85;% 训练集占85%
mlp_models.divideParam.valRatio = 0.15;% 验证集占15%
% 创建一个有35个隐藏层节点的模式识别神经网络,训练函数为'trainrp'(反向传播)
mlp_models = patternnet(35, 'trainrp');
mlp_models.trainParam.lr = 0.004;% 设置学习率为0.004
mlp_models.trainParam.mc = 0.35;% 设置动量系数为0.35
% 设置第一层的传递函数为'transig'(Sigmoid函数)
mlp_models.trainParam.epochs=300;% 设置训练次数为300次
tic% 开始计时,计算模型训练时间。% 使用训练数据进行训练,结果存储在net中,同时返回训练记录tr,预测输出y和误差e。
..........................................................................
figure
plot(xSVM,ySVM,'r')
hold on
plot(xMLP,yMLP,'b')
legend('SVM','MLP')
xlabel('FP');
ylabel('TP');
title('ROC曲线')
grid onfigure
bar([aucSVM,aucMLP]);
xlabel('模型类型');
ylabel('R auc');
xticklabels({'SVM','MLP'});
ylim([0.75,1]);
674.算法理论概述
支持向量机(SVM)和多层感知器(MLP)是两种常用的机器学习算法,它们在数据预测和分类任务中都有广泛的应用。下面将详细介绍这两种算法的原理和数学公式。
一、支持向量机(SVM)
支持向量机是一种二分类算法,其基本思想是在特征空间中找到一个最优超平面,使得该超平面能够将不同类别的数据点尽可能地分开。具体来说,对于一个二分类问题,假设数据集包含n个样本{(x1, y1), (x2, y2), ..., (xn, yn)},其中xi是输入特征向量,yi是对应的类别标签(+1或-1)。SVM的目标是找到一个最优超平面wx+b=0,使得该超平面能够将不同类别的数据点尽可能地分开,同时使得超平面两侧的空白区域(即“间隔”)最大化。
在数学上,SVM的优化问题可以表示为以下形式:
min 1/2 ||w||^2 + C ∑ ξ_i
s.t. y_i (w^T x_i + b) ≥ 1 - ξ_i, i=1,2,...,n
ξ_i ≥ 0, i=1,2,...,n
其中,w是超平面的法向量,b是超平面的截距,C是一个惩罚参数,用于控制误分类的惩罚力度,ξ_i是第i个样本的松弛变量,用于容忍一些不可分的样本。该优化问题的目标是最小化超平面的法向量长度(即||w||^2)和误分类的惩罚项(即C ∑ ξ_i)。
对于非线性可分的情况,可以通过核函数将输入特征映射到高维空间,使得在高维空间中数据变得线性可分。此时,优化问题中的内积运算需要用核函数来替代。常见的核函数包括线性核、多项式核和高斯核等。
二、多层感知器(MLP)
多层感知器是一种前向传播的神经网络,其基本结构包括输入层、隐藏层和输出层。在数据预测任务中,MLP通过学习输入数据和输出数据之间的非线性映射关系,来对新的输入数据进行预测。具体来说,对于一个回归问题,假设数据集包含n个样本{(x1, y1), (x2, y2), ..., (xn, yn)},其中xi是输入特征向量,yi是对应的输出值。MLP的目标是找到一个最优的网络参数θ,使得对于任意一个新的输入x,都能够输出一个尽可能接近真实值y的预测值。
在数学上,MLP的预测过程可以表示为以下形式:
y_pred = f(x; θ)
其中,f(·)表示MLP的网络结构,θ表示网络参数。通常,MLP的网络结构包括多个隐藏层和非线性激活函数,如ReLU、sigmoid或tanh等。网络参数的优化通常采用梯度下降算法及其变种,如批量梯度下降、随机梯度下降和小批量梯度下降等。在训练过程中,通过反向传播算法计算损失函数对网络参数的梯度,并根据梯度更新网络参数,以最小化预测误差。常见的损失函数包括均方误差损失、交叉熵损失等。
需要注意的是,MLP的训练过程容易陷入局部最优解和过拟合等问题。为了避免这些问题,可以采用一些正则化技术,如L1正则化、L2正则化和dropout等。此外,还可以采用一些集成学习技术,如bagging和boosting等,以提高模型的泛化能力和鲁棒性。
5.算法完整程序工程
OOOOO
OOO
O