文章目录
- 前言
- 线性表
- 顺序表
- 链表
- 合并有序链表
- 反转链表
- 队列
- 循环队列
- 双端队列
- 资源分配问题
- 栈
- 共享栈
- 表达式求值
- 递归处理
- 迷宫问题
- 串
- 串的模式匹配
- BF算法
- KMP算法
- next数组的求解
- next数组的优化
前言
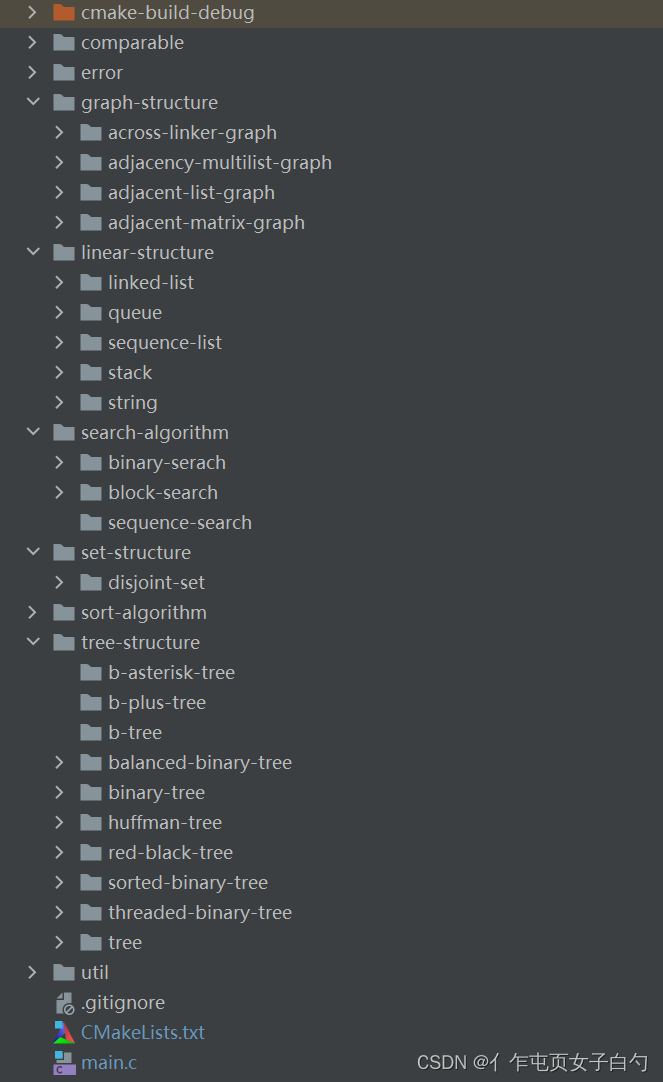
本文所有代码均在仓库中,这是一个完整的由纯C语言实现的可以存储任意类型元素的数据结构的工程项目:
线性表
线性表是具有相同类型 n n n个数据元素的有限序列:
L = ( a 1 , a 2 , … , a n ) L=(a_1,a_2,\dots,a_n) L=(a1,a2,…,an)
其中 n n n为表长,当 n = 0 n=0 n=0时线性表是一个空表,数据元素在线性表的位置称为位序(从 1 1 1开始)。线性表的性质如下:
- 线性表中存在唯一的第一元素也存在唯一的最后元素。
- 除第一元素外,其它元素有唯一的直接前驱,除最后元素外,其它元素有唯一的直接后继。
顺序表
使用顺序存储方式实现的线性表称为顺序表。顺序表的特点如下:
- 随机访问:可以在 O ( 1 ) O(1) O(1)时间内找到第 i i i个元素。
- 存储密度高:每个节点只存储数据元素。
- 扩展容量不方便。
- 插入、删除元素不方便,需要移动大量元素。
struct SequenceList{ElementType * data;int length;
};
链表
使用链式存储实现的线性表称为链表。链表由若干个节点连接而成。每个节点包括两部分一部分是存储数据元素的数据域,另一部分是存储其它节点地址的指针域。链表的特点如下:
- 链表的访问是顺序的,只能通过头指针进行。
- 链表可以有一个头节点,也可以没有,头节点不存储任何数据,含有头节点的链表操作更加方便。
- 除头节点外第一个存储数据的节点称为首元节点。
只有一个指针域的链表称为单链表:
//SingleLinkedList.h
typedef struct Node Node, *SingleLinkedList;
//SingleLinkedList.c
struct Node {ElementType data;struct Node *next;
};
有两个指针域的链表称为双链表:
//DoubleLinkedList.h
typedef struct Node Node, *DoubleLinkedList;
//DoubleLinkedList.c
struct Node {ElementType data;struct Node *last;struct Node *next;
};
把单链表和双链表的第一元素和最后元素就变成了循环链表。
合并有序链表
SingleLinkedList mergeOrderedLinkedList(SingleLinkedList l1, SingleLinkedList l2) {//返回最小的节点if (l1 == NULL) {return l2;} else if (l2 == NULL) {return l1;} else if (l1->data < l2->data) {l1->next = mergeOrderedLinkedList(l1->next, l2);return l1;} else {l2->next = mergeOrderedLinkedList(l1, l2->next);return l2;}
}
反转链表
- 反转整个链表
SingleLinkedList reverseList(SingleLinkedList list) {if (list->next==NULL){return list;} else{Node * head=reverseList(list->next);list->next->next=list;list->next=NULL;return head;}
}
- 反转链表的前n个元素
public ListNode end;
public ListNode reverseListN(ListNode head,int n){if (n==1){end=head.next;return head;}else {ListNode newHead=reverseListN(head.next,n-1);head.next.next=head;head.next=end;return newHead;}
}
反转链表的任意一部分
public ListNode reverseBetween(ListNode head, int left, int right) {if (left==1){return reverseListN(head,right);}else {head.next=reverseBetween(head.next,left-1,right-1);return head;}
}
k个一组反转链表
public ListNode reverseKGroup(ListNode head, int k) {if (k==1){return head;}else {ListNode right=head;for (int i = 1; i < k; i++) {if (right==null){return head;}right=right.next;}ListNode newHead=reverse(head,right);if (right!=null&&right.next!=null){head.next=reverseKGroup(head.next,k);}return newHead;}
}
public ListNode end;
public ListNode reverse(ListNode left,ListNode right){if (left==null||right==null||left==right){return left;} {end=right.next;ListNode newHead = reverse(left.next, right);left.next.next=left;left.next=end;return newHead;}
}
队列
队列是一种只能在表头或表尾进行插入或删除的线性表,它的特点如下:
- 插入元素的一端称为队尾
- 删除元素的一端称为队头
- 遵循先入先出原则
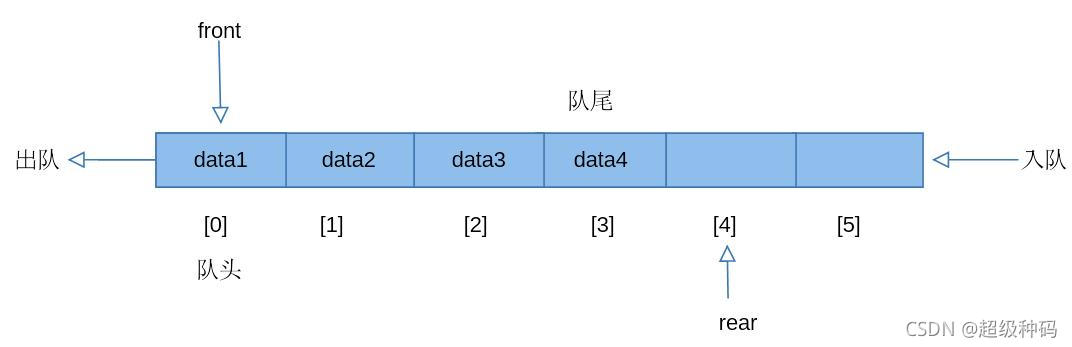
可以使用顺序存储或链式存储的方式实现队列:
//顺序存储
typedef struct SequenceQueue SequenceQueue;
struct SequenceQueue {ElementType data[MAX_SIZE];int front;int rear;
};//链式存储
#include "../linkList/SingleLinkedList.h"
typedef struct LinkedQueue LinkedQueue;
struct LinkedQueue {Node *front;Node *rear;
};
循环队列
双端队列
资源分配问题
栈
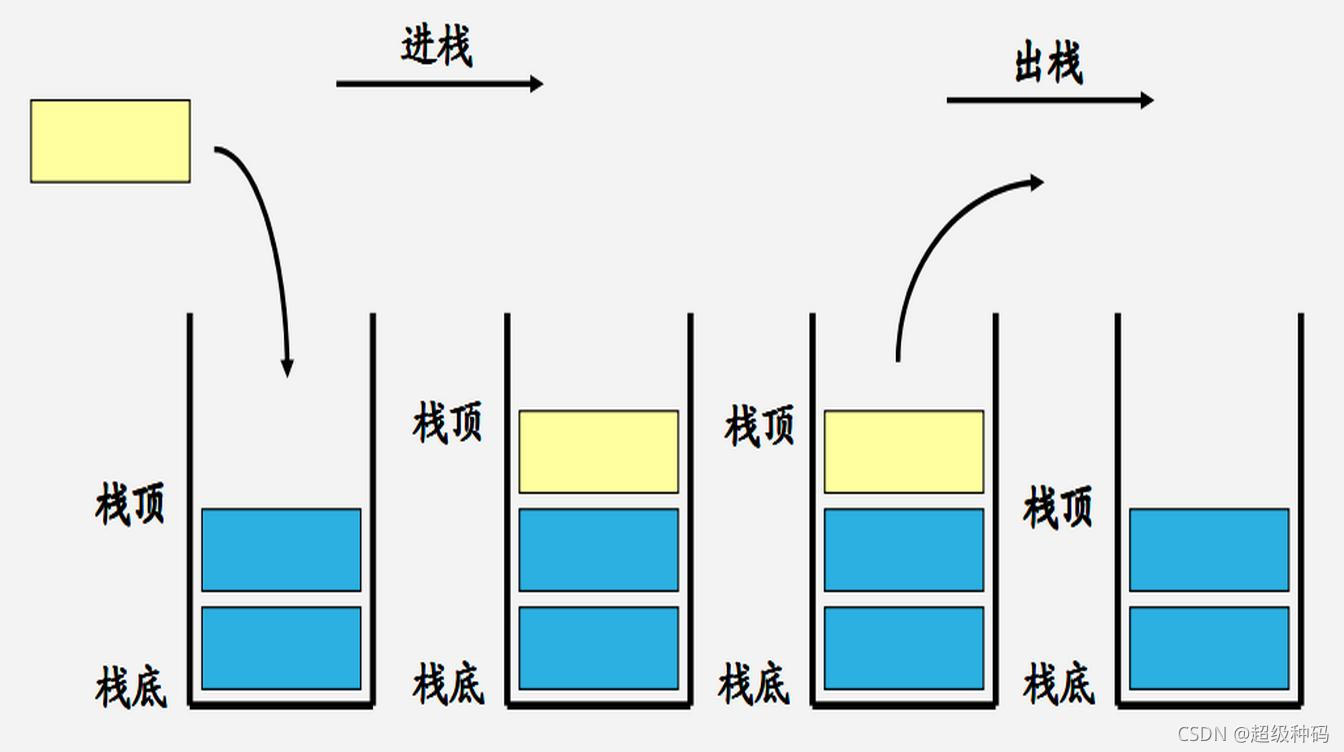
栈是一种只能在表头或表尾进行插入和删除的线性表。它的特点如下:
- 允许插入和删除的一端称为栈顶
- 不允许插入和删除的一端称为栈底
- 遵循先入后出原则
- n n n个不同元素进栈,出栈元素不同排列个数为 1 n + 1 C 2 n n \frac{1}{n+1}C^n_{2n} n+11C2nn(卡特兰数)
可以通过顺序存储和链式存储的方式实现栈:
//顺序存储
typedef struct SequenceStack SequenceStack;
struct SequenceStack {ElementType data[MAX_SIZE];int top;
};//链式存储
typedef struct Node Node, *LinkedStack;
struct Node{ElementType data;struct Node * next;
};
共享栈
表达式求值
- 中缀表达式
- 后缀表达式(逆波兰表达式):
- 左优先原则:只要左边的运算符能先算,就先算左边的
- 先出栈的是右操作数
- 前缀表达式(波兰表达式):
- 右优先原则:只要右边的运算符能先算,就优先算右边的
- 先出栈的是左操作数
递归处理
迷宫问题
串
串是一个数据元素只能是字符的线性表:
S = ′ a 1 a 2 … a n ′ S='a_1a_2\dots a_n' S=′a1a2…an′
其中 n n n为串长,当 n = 0 n=0 n=0时串为空串。串中任意连续字符组成的子序列称为该串的子串,包含该子串的串称为主串,不包含串本身的子串称为真子串,空串是任意串的子串。某个字符在串中的序号称为该字符在串中的位置。子串在主串中的位置以子串的第一个字符在主串中的位置来表示。
//String.h
typedef struct String *String;//String.c
struct String {char *ch;int length;
};
串的模式匹配
子串在串中的定位称为串的模式匹配。通常有以下两种算法:
- BF算法
- KMP算法
BF算法
BF算法也称为简单匹配法,它的算法思想是:将主串中所有与模式串长度相同的子串和模式串对比,直到找到一个完全匹配的子串或所有的子串都不匹配为止。
int BF(String src, String target) {int i = 1, j = 1;while (i <= src->length && j <= target->length) {if (*(src->ch + i - 1) == *(target->ch + j - 1)) {i++;j++;} else {i = i - j + 2;j = 1;}}if (j > target->length) {return i - target->length;} else {return 0;}
}
KMP算法
与BP算法相比KMP算法可以利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配。首先弄清三个概念:
- 前缀:除最后一个字符外,字符串的所有头部子串。
- 后缀:除第一个字符外,字符串的所有尾部子串。
- 部分匹配:字符串最长相等前后缀的长度。
下面通过以下两个串来描述算法:
//主串:aaabaaaabaa
String src=stringConstructor("aaabaaaabaa");
//模式串:aabaa
String target=stringConstructor("aabaa");
算法开始时先求出模式串中以各个字符为结尾的子串的部分匹配值,并将这些值放到数组partialMarch中:
//a:0
//aa:1
//aab:0
//aaba:1
//aabaa:2
int partialMarch[]={,0,1,0,1,2};//字符串的位置从1开始,数组下标从0开始,为了便于计算,舍弃数组的第一位
当匹配失败时,主串不再回溯而是保持当前位置不动,模式串也不再从头开始,而是相对于当前位置回退move位,回退之后继续匹配,move由以下公式计算:
//回退位数=匹配成功子串的字符个数-匹配成功子串的部分匹配值
//j为模式串当前匹配的位置
move=(j-1)-partialMarch[j-1]
从partialMarch数组的角度看就是当前字符匹配失败就会找它前一个字符的部分匹配值,因此最后一个字符的部分匹配值将永远用不到,所以可以将partialMarch数组整体向右移动一个单位得到next数组(第一个元素以-1填充):
next[]={,-1,0,1,0,1};
那么move就变为:
move=(j-1)-next[j]
那么回退后的j就变为:
j=j-move=next[j]+1
如果将next数组各个元素加1:
next[]={,0,1,2,1,2};
此时j为:
j=next[j]
next数组的求解
因此最主要的任务就是求解next数组,原理很简单,设i为模式串的当前位置,j为上一位置的next数组值,即j=next[i-1],那么:
- 当
i=1时,next[i]≡0; - 当
i≠1时:- 如果
charAt(target, i) == charAt(target, j),那么next[i]=j+1; - 如果
charAt(target, i) == charAt(target, j),那么就让j=next[j],之后继续比较,直至比较相等或j=0。
- 如果
int *getNext(String target) {int *next = calloc(target->length + 1, sizeof(int));*(next + 1) = 0;int i = 1, j = 0;while (i < target->length) {if (j == 0 || charAt(target, i) == charAt(target, j)) {next[++i] = ++j;} else {j = next[j];}}
}
// 初始:i=1,j=0
// | i |1|2|3|4|5|
// |target|a|a|b|a|a|
// | next |0| | | | |// 第一轮:i=1,j=0
// | i |1|2|3|4|5|
// |target|a|a|b|a|b|
// i=2,j=1
// | next |0|1| | | |// 第二轮:i=2,j=1
// | i |1|2|3|4|5|
// |target|a|a|b|a|b|
// i=3,j=2
// | next |0|1|2| | |// 第三轮:i=3,j=2
// | i |1|2|3|4|5|
// |target|a|a|b|a|b|
// i=4,j=1
// | next |0|1|2|1| |//第四轮:i=4,j=1
// | i |1|2|3|4|5|
// |target|a|a|b|a|b|
// i=5,j=2
// | next |0|1|2|1|2|
next数组的优化
可以对next数组进一步优化,当计算出next[++i]后,如果发现*charAt(target, i) == charAt(target, next[i]),那么下一次比较必将失败,此时就可以将next[i] = next[next[i]]。
int *getNextVal(String target) {int *nextVal = calloc(target->length + 1, sizeof(int));*(nextVal + 1) = 0;int i = 1, j = 0;while (i < target->length) {if (j == 0 || charAt(target, i) == charAt(target, j)) {nextVal[++i] = ++j;if (charAt(target, i) == charAt(target, nextVal[i])) {nextVal[i] = nextVal[nextVal[i]];}} else {j = nextVal[j];}}
}
完整的KMP算法如下:
int enKMP(String src, String target) {int *next = getNextVal(target);int i = 1, j = 1;while (i <= src->length && j <= target->length) {if (j == 0 || charAt(target, i) == charAt(target, j)) {i++;j++;} else {j = *(next + j);}}if (j > target->length) {return i - target->length;} else {return 0;}
}





](https://img-blog.csdnimg.cn/34f25434e13641d3a138f929d859c0fc.png)