【重拾C语言】十二、C语言程序开发（穷举与试探—

【重拾C语言】十二、C语言程序开发（穷举与试探——八皇后问题）

前言

十二、C语言程序开发

12.1~3 自顶向下、逐步求精；结构化程序设计原则；程序风格

12.4 八皇后——穷举与试探

12.4.1 穷举法

示例：寻找一个整数的平方根

12.4.2 试探法

示例：计算给定数字的阶乘

12.4.3 穷举与试探（八皇后问题）-递归实现

前言

八皇后问题是一个经典的计算机科学问题，要求在一个8×8的棋盘上放置8个皇后，使得它们互相之间不能攻击到对方。这个问题可以通过穷举和试探的方法来解决。

穷举法是一种解决问题的方法，它通过尝试所有可能的解决方案来找到满足条件的解。这种方法适用于解空间较小的问题，例如八皇后问题、0/1 背包问题等。在 C 语言中，我们可以通过编写循环来遍历所有可能的解决方案，并判断是否满足条件。
试探法是一种基于经验或启发式规则的方法，它通过逐步搜索解空间来找到满足条件的解。这种方法适用于解空间较大或问题具有启发式特征的情况。在 C 语言中，我们可以通过编写递归或循环来实现试探法，例如深度优先搜索（DFS）或广度优先搜索（BFS）。

十二、C语言程序开发

12.1~3 自顶向下、逐步求精；结构化程序设计原则；程序风格

【重拾C语言】十二、C语言程序开发（自顶向下、逐步求精；结构化程序设计原则；程序风格）_QomolangmaH的博客-CSDN博客https://blog.csdn.net/m0_63834988/article/details/133825033?spm=1001.2014.3001.5502 在C语言程序开发中，可以使用自顶向下、逐步求精的方法解决问题，遵循结构化程序设计原则，同时注重良好的程序风格，这可以帮助开发者编写可读性强且易于维护的代码。

12.4 八皇后——穷举与试探

12.4.1 穷举法

穷举法（Exhaustive Search）是一种常见的算法设计方法，用于在给定的搜索空间中尝试所有可能的解决方案，以找到满足特定条件的解。

在C语言中，可以使用循环结构和条件语句来实现穷举法。一般步骤如下：
- 定义问题的搜索空间和解的表示方式。
- 使用循环结构遍历搜索空间中的所有可能解。
- 对于每个可能解，使用条件语句判断是否满足问题的条件。
- 如果满足条件，执行相应的操作，例如输出结果或保存解决方案。
- 继续循环，直到遍历完整个搜索空间。
示例：寻找一个整数的平方根

#include <stdio.h>int main() {int num;printf("Enter a number: ");scanf("%d", &num);int i;for (i = 0; i <= num; i++) {if (i * i == num) {printf("Square root of %d is %d\n", num, i);break;}}if (i > num) {printf("No square root found for %d\n", num);}return 0;
}

通过循环遍历从0到输入的数字，逐个尝试每个可能的平方根。如果找到一个平方根，就输出结果并结束循环。如果循环结束后仍然没有找到平方根，就输出相应的提示信息。

输出：

这只是一个简单的示例，实际上，穷举法可以应用于各种问题，包括组合优化、密码破解等。但是需要注意的是，穷举法的计算复杂度通常较高，随着搜索空间的增大，计算时间会呈指数级增长。因此，在实际应用中，需要根据问题的规模和要求，权衡计算时间和解的准确性。

12.4.2 试探法

试探法（Backtracking）是一种基于经验或启发式规则的方法，它通过逐步搜索解空间来找到满足条件的解。通常通过递归的方式进行搜索，尝试每一种可能的选择，并在满足条件的情况下继续向下搜索，如果不满足条件，则回溯到上一步选择的状态，重新选择其他可能的路径。

在C语言中，可以使用递归函数和条件语句来实现试探法。一般步骤如下：
- 定义问题的搜索空间和解的表示方式。
- 编写一个递归函数，在每一步选择中进行尝试，并根据条件判断是否满足问题的要求。
- 如果满足条件，执行相应的操作，例如输出结果或保存解决方案。
- 继续递归调用函数，进入下一步选择。
- 如果不满足条件，回溯到上一步选择的状态，重新选择其他可能的路径。
- 继续递归调用函数，进行下一步尝试。
示例：计算给定数字的阶乘

#include <stdio.h>int factorial(int n) {// 基本情况：当 n 为 0 或 1 时，阶乘为 1if (n == 0 || n == 1) {return 1;}// 递归情况：调用自身来计算 n 的阶乘else {return n * factorial(n - 1);}
}int main() {int n = 5;int result = factorial(n);printf("%d 的阶乘为 %d\n", n, result);return 0;
}

输出：

试探法可以应用于各种问题，如组合优化、图的遍历、八皇后问题等。通过不断地试探和回溯，可以找到所有可能的解决方案。请注意，试探法的计算复杂度也可能较高，特别是在搜索空间较大时。因此，在实际应用中，需要谨慎选择搜索策略和剪枝技巧，以提高算法的效率。同时，合理设计问题的表示方式和条件判断，可以帮助减少搜索空间，加快求解过程。

12.4.3 穷举与试探（八皇后问题）-递归实现

穷举法是一种简单但低效的解决方法，它通过尝试所有可能的皇后布局来找到满足条件的解。具体步骤如下：

从第一行开始，依次尝试在每一列放置皇后。
检查当前的布局是否满足没有皇后互相攻击的条件。
如果满足条件，继续到下一行，重复上述步骤。
如果在某一行无法找到合适的位置放置皇后，回溯到上一行，尝试下一个列。
当放置完最后一行的皇后并且满足条件时，找到一个解。

穷举法的缺点是需要尝试大量的组合，因此在较大的棋盘上效率较低。

#include <stdio.h>#define N 8void printBoard(int board[N][N]) {for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {printf("%c ", board[i][j] ? 'Q' : '.');}printf("\n");}printf("\n");
}int isSafe(int board[N][N], int row, int col) {// 检查当前位置的左侧是否有皇后for (int i = 0; i < col; i++) {if (board[row][i]) {return 0;}}// 检查当前位置的左上方是否有皇后for (int i = row, j = col; i >= 0 && j >= 0; i--, j--) {if (board[i][j]) {return 0;}}// 检查当前位置的左下方是否有皇后for (int i = row, j = col; i < N && j >= 0; i++, j--) {if (board[i][j]) {return 0;}}return 1;
}
int count = 0; // 全局变量用于计数解的数量
void solveNQueens(int board[N][N], int col) {// 所有皇后都放置完毕，打印解决方案，增加解的数量并返回if (col == N) {printBoard(board);count++;return;}// 逐行尝试放置皇后for (int i = 0; i < N; i++) {if (isSafe(board, i, col)) {// 放置皇后board[i][col] = 1;// 递归地尝试下一列solveNQueens(board, col + 1);// 回溯，撤销当前位置的皇后board[i][col] = 0;}}
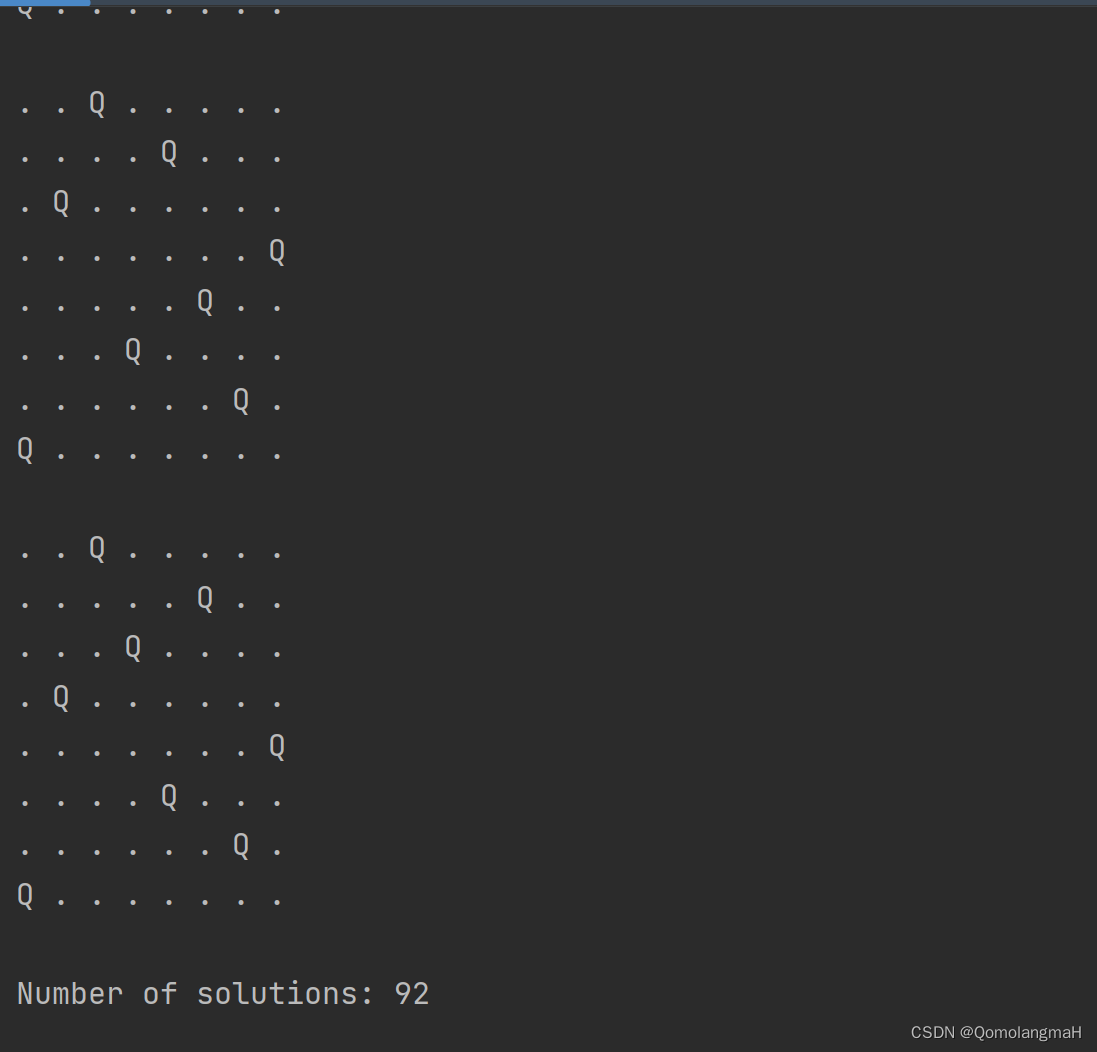
}int main() {int board[N][N] = {0};solveNQueens(board, 0);printf("Number of solutions: %d\n", count);return 0;
}

输出：