当`npm publish`发布时,控制台提示:`Scope not found`,具体错误信息如下:
npm notice npm ERR! code E404 npm ERR! 404 Not Found - PUT https://registry.npmjs.org/@xxx%2fxxx - Scope not found npm ERR! 404 npm ERR! 404 '@xxx/xxx@0.0.0' is not in this registry. npm ERR! 404 You should bug the author to publish it (or use the name yourself!) npm ERR! 404 npm ERR! 404 Note that you can also install from a npm ERR! 404 tarball, folder, http url, or git url. npm ERR! A complete log of this run can be found in: npm ERR! C:\Users\Administrator\AppData\Local\npm-cache\_logs\2021-12-06T14_56_55_018Z-debug.log这是由于包名是`@xxx/xxx`形式造成的。如果包名是`@`开头,需要到npm官网先创建一个组织。
**具体步骤如下:**
1. 注册`npm`官网账号,并且进入个人中心
2. 看到页面左侧菜单栏,点击后面的加号

3. 进入创建组织页面,输入组织名称。(这里不需要加上`@`符号)
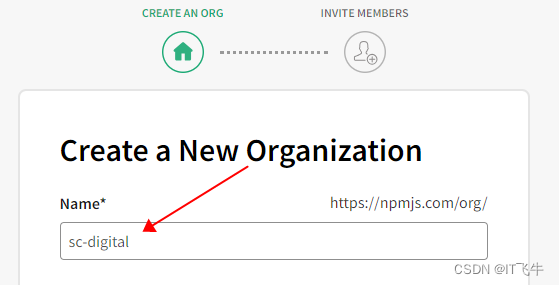
如果组织名称已经存在页面会提示:

4. 再次执行`npm publish`命令,这是就可以正常发布。