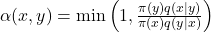来自Manolis Kellis教授（MIT计算生物学主任）的课
油管链接：6.047/6.878 Lecture 7 - RNA folding, RNA world, RNA structures (Fall 2020)
本节课分为三个部分，本篇笔记是第三部分RNA folding。
本课程探讨RNA的折叠过程及其预测方法。先了解了RNA的表示和Nussinov算法的应用。然后通过动态规划预测复杂的RNA叠加与折叠。最后介绍了随机上下文无关文法，为RNA结构提供了广泛的描述框架。

RNA折叠

RNA折叠是一个过程，其中RNA分子将自己折叠成特定的三维结构，这些结构对于其功能至关重要。

RNA folding representation

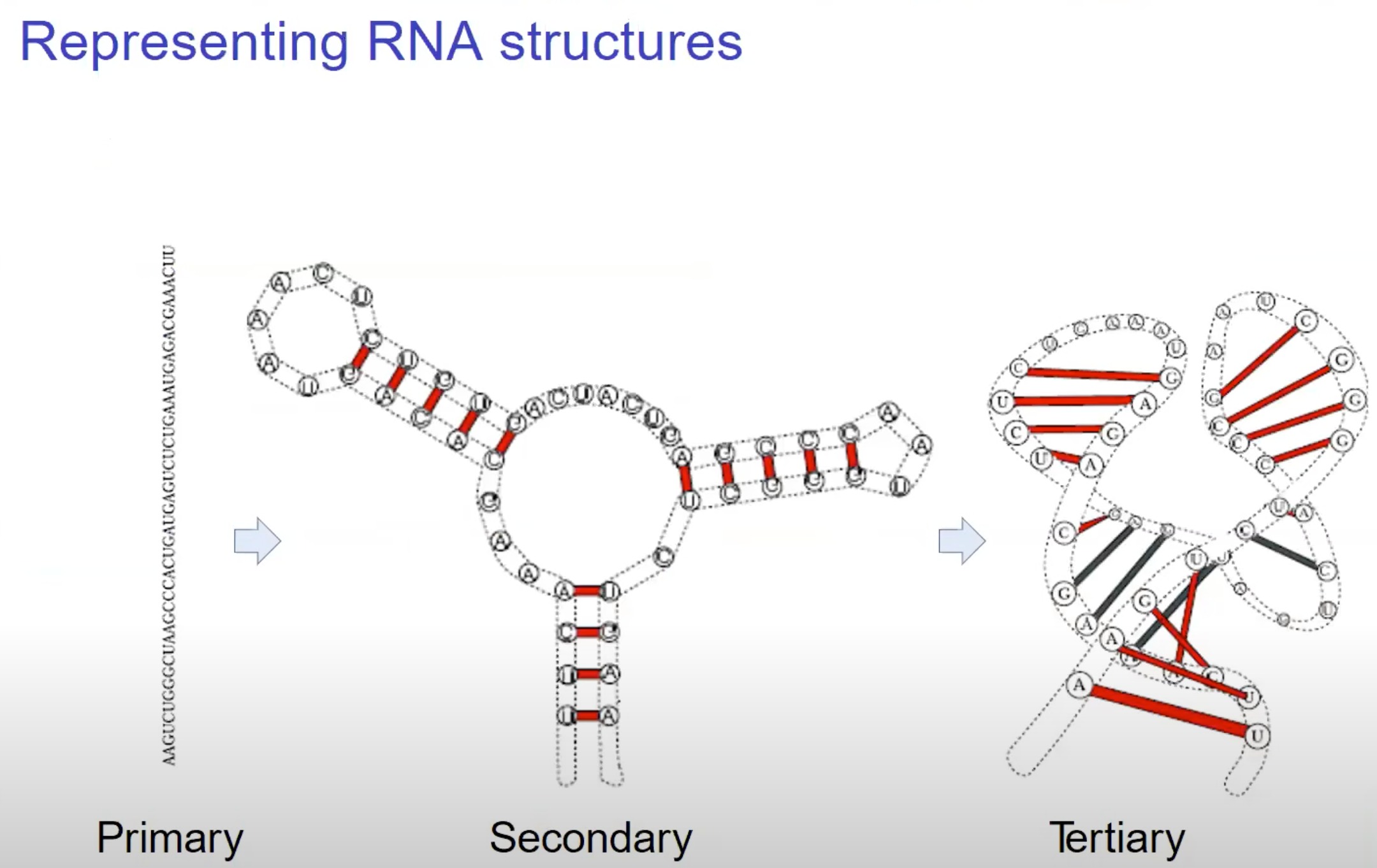
1. 初级结构 (Primary)
2. 二级结构 (Secondary): 二级结构展示了RNA分子如何在空间中折叠并通过氢键形成基对。tRNA和rRNA就是依赖其二级结构来发挥作用的。
   • 某些RNA的功能区域可能是由其特定的二级结构模式决定的。
3. 三级结构 (Tertiary): 三级结构描述了RNA分子如何进一步在三维空间中折叠，以形成更复杂的结构。在这一级，分子的不同部分可能会通过疏水相互作用、范德华力和其他非共价相互作用来相互接触。

1. 能量的覆盖: RNA二级结构占据了折叠过程中的大部分自由能。这意味着RNA的稳定性和形成方式在很大程度上取决于其二级结构。
2. 生化粗粒化: RNA的二级结构为我们提供了一个粗略的、生化上有意义的3D结构表示。这使得研究人员可以更容易地理解RNA的空间排布和功能性质。
3. 折叠的中间态: 在形成其完整的三维结构之前，RNA首先会形成一个稳定的二级结构。这是RNA折叠成其最终功能形态的关键步骤。
4. 进化上的保守性: 在进化过程中，RNA的二级结构往往是保守的。这意味着相似的二级结构在不同的生物中可能具有相似的功能。
5. 易于计算处理: 与RNA的完整三维结构相比，其二级结构相对简单，因此更容易在计算机上建模和分析。

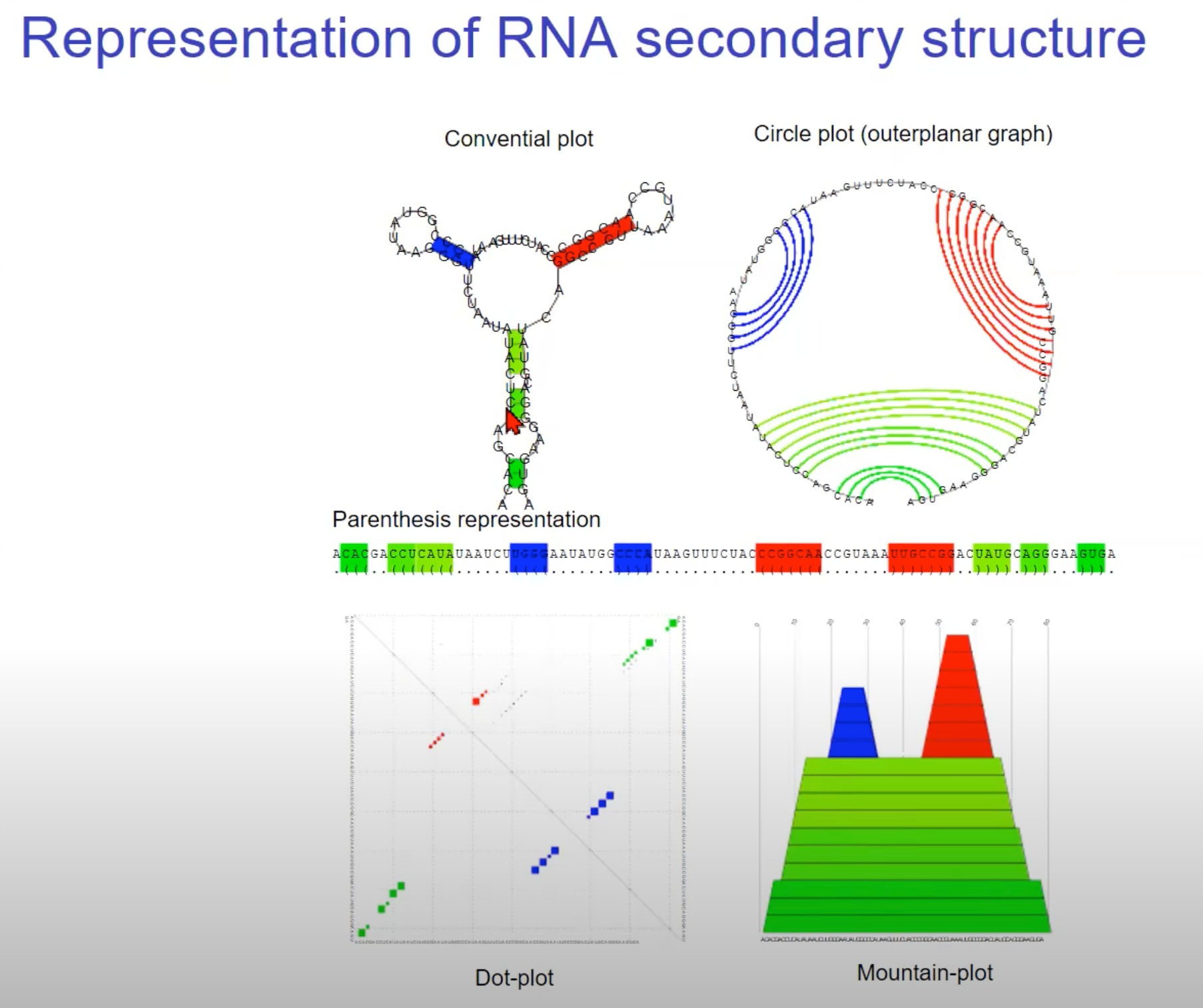
这个图展示了RNA二级结构的不同表示方法。以下是每种表示方法的简要解释：

1. 常规图（Conventional plot）: 这种图形展示了RNA分子的实际形状和其碱基配对。

2. 圆形图（Circle plot/outerplanar graph）: 这是RNA二级结构的另一种表示方法，其中RNA序列被放置在一个圆上，碱基配对则由连接线表示。这种方法适用于显示复杂的或交叉的碱基配对关系。

3. 括号表示法（Parenthesis representation）: 在这种表示法中，RNA序列从左到右写出，而碱基配对则通过括号表示。匹配的左括号和右括号表示一对碱基配对，而点表示未配对的碱基。这种表示法非常紧凑，适用于计算和算法处理。

4. 点图（Dot-plot）: 点图显示了RNA序列内部所有可能的碱基配对。图上的每个点代表一个特定的碱基配对。这种方法常用于预测RNA二级结构和比较不同结构的相似性。

5. 山形图（Mountain-plot）: 这种表示法通过高度变化来描绘RNA的二级结构。高度的变化反映了RNA结构中的堆叠区域。这提供了一个直观的方式来了解RNA的叠层结构和拓扑形态。

1 DP for simple folds

使用动态规划（Dynamic Programming）来解决RNA折叠问题。RNA折叠是预测RNA分子在三维空间中如何折叠成其稳定的结构的问题。

• 当RNA分子折叠时，某些碱基对之间会形成氢键，形成了所谓的碱基配对。我们通常希望优化的是整个结构的稳定性，这可以通过计算配对得分来评估
• 参考我们前面序列对比的动态规划，尝试应用在这里

1.1 Nussinov Algorithm objective

算法目标：预测RNA的二级结构

• Objective function（目标函数）:

  • Nussinov算法的目标是找到具有最大嵌套配对数的RNA结构。所谓的嵌套配对意味着这些配对不与其他配对交叉。

• Recursive computation（递归计算）:

  • Use dynamic programming?
  • How?：具体实施方式涉及建立一个得分矩阵，并通过考虑RNA序列中每个可能的碱基对来填充这个矩阵。每个位置的得分都是基于它可以形成的最佳配对，以及它与其他碱基之间的关系。

• Similarities to sequence alignment（与序列比对的相似性）:

  • 在序列比对中，我们试图找到两个或多个序列之间的最佳对齐方式。对于RNA结构预测，我们试图找到RNA序列内部的最佳对齐方式，即碱基配对方式。

1.2 energy constraints

RNA folding based on biophysical energy constraints（基于生物物理能量约束的RNA折叠）

1. Scoring scheme（评分方案）:

   • 为了决定RNA的最优结构，这里有一个评分系统。在物理上，结构的优化通常是基于最小自由能的。自由能在这里代表稳定性，较低的自由能意味着更稳定的结构。
   • 
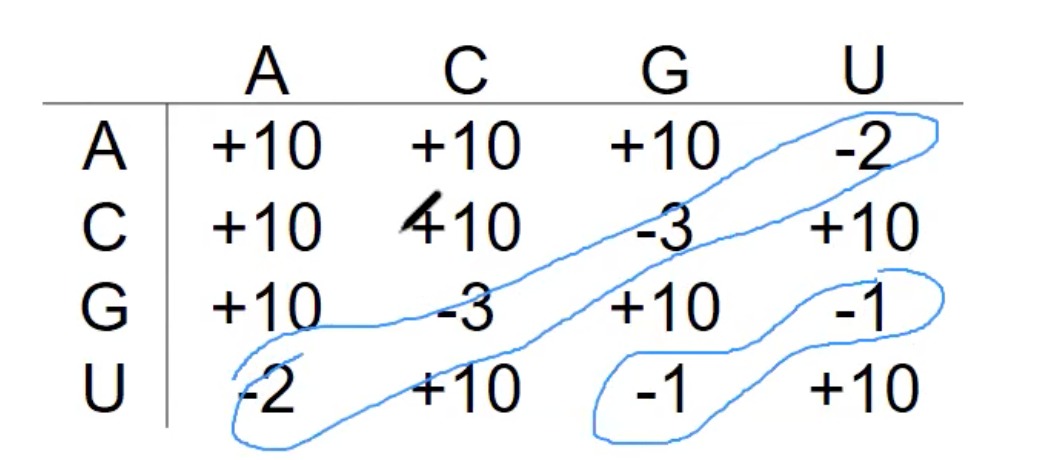
     • "-1"表示G和U的配对，特殊
   • 为了简化模型，为每对碱基配对分配了一个能量值。例如，A与U的配对有-2的能量值，而C与G的配对有-3的能量值。这些值可能是基于实验数据的。

2. Does DP apply?（动态规划是否适用？）:

   • 考虑到能量分数是可加的。
   • 稍后可能会讨论更复杂的能量模型，但基本的思路是，通过排除某些结构（如伪节点），可以将问题分解为子问题，这使得动态规划变得可行。

3. Define “matrix”: Eij:

   • 这定义了一个矩阵E，其中Eij表示子序列i到j之间的最小能量。
   • 这个矩阵用于动态规划算法，储存每个子序列的最优解，从而避免重复计算。

4. Recursion formula（递归公式） 和 Traversal order（遍历顺序）

通过为每对碱基配对分配能量分数，并使用动态规划来找到具有最低总自由能的结构，我们可以获得RNA的预测结构。

1.3 The key idea of the algorithm

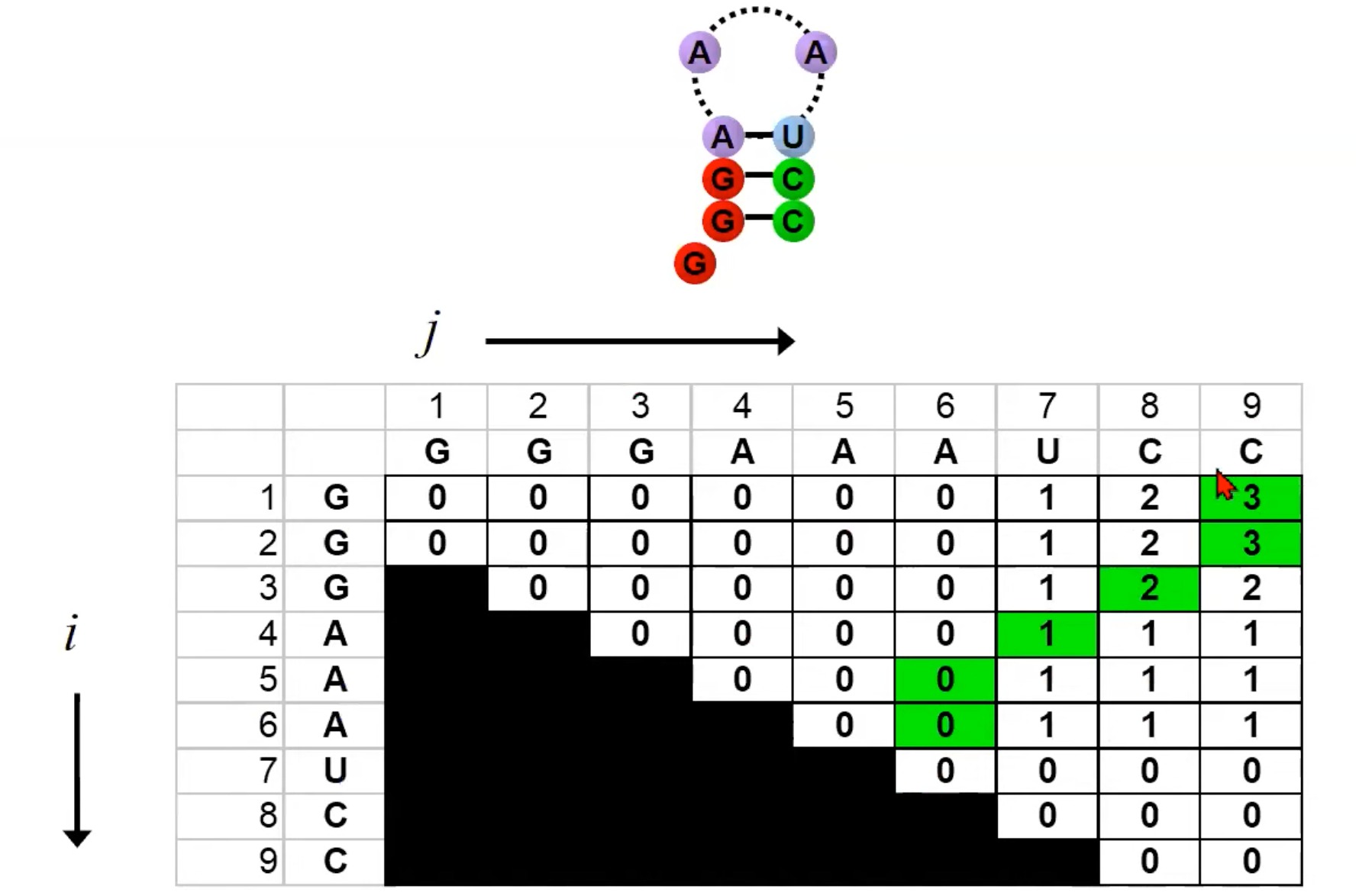
右侧的图显示了一个填充了数字的大矩阵。这个矩阵的填充表示算法的动态规划过程。每个矩阵的单元格代表一个RNA子序列的得分。为了找到整个RNA序列的最优二级结构，算法会逐步填充这个矩阵。

1. 矩阵的对角线：矩阵的对角线上的值都是0，因为一个单独的碱基不能与自己形成配对，所以得分为0。

2. 填充顺序：可以看到图中的蓝色箭头，这表示填充矩阵的顺序。算法从对角线开始，然后向右上方移动，填充每一个子矩阵。

3. 碱基配对：在图中，有些地方用线连接了两个点。这表示在那个特定的RNA子序列中，两个碱基形成了配对。

4. 计算得分：当计算F(i, j)时，我们会查看以下两种情况：

   1. i和j配对的得分（如果它们可以配对的话）加上子序列F(i+1, j-1)的得分。
   2. 不考虑i和j的配对，而是查看从i到j之间所有可能的分割点k，然后取F(i, k)和F(k+1, j)的得分之和的最大值。
   3. 下一个遍历是往右上角遍历

5. 该矩阵的填充反映了RNA序列的所有可能的二级结构。算法通过比较所有这些可能性来找到得分最高的结构。

1. $i,j$配对:

   • 在这种情况下，位置$i$的碱基与位置$j$的碱基形成了配对，因此它们之间形成了一个碱基对。
   • 同时，子序列 $x_{i+1}$ 到 $x_{j-1}$ 可能还有其他的最佳配对，记为 $F(i+1,j-1)$。

2. $i$未配对:

   • 在这里，位置$i$的碱基没有与任何其他碱基配对。
   • 子序列 $x_{i+1}$ 到 $x_j$ 继续寻找其他可能的最佳配对。

3. $j$未配对:

   • 与“$i$未配对”的情况类似，这里位置$j$的碱基没有与任何其他碱基配对。
   • 子序列 $x_i$ 到 $x_{j-1}$ 继续寻找其他可能的最佳配对。

4. 分叉:

   • 在这种情况中，序列在某个位置$k$处被分成了两部分。
   • 从 $x_i$ 到 $x_k$ 的子序列和从 $x_{k+1}$ 到 $x_j$ 的子序列分别寻找自己的最佳配对。
   • 这是一个更复杂的情况，因为我们需要考虑从$i$到$j$之间的所有可能的$k$值，并为每个$k$值计算其得分 $F(i,k)+F(k+1,j)$。最后，我们选择使得 $F(i,j)$ 得分最大的$k$值。

2 DP for stacking and complex folds

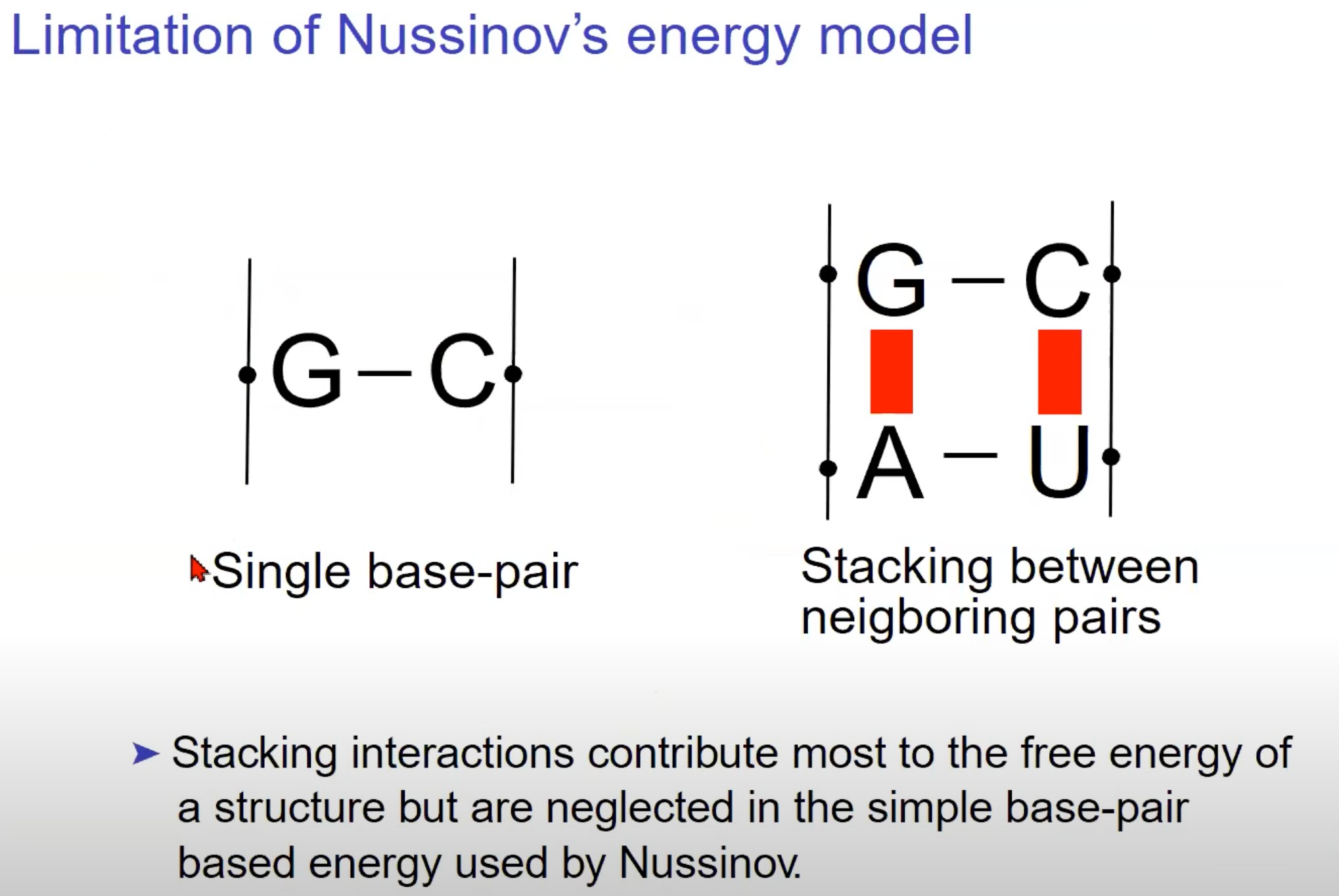
Nussinov能量模型的局限性

• 除了单个碱基对外，RNA碱基还倾向于在空间中堆叠，形成堆叠结构。这里显示了一个G-C配对和一个A-U配对的堆叠。堆叠交互是由于相邻碱基对之间的香族环的π-π交互。
• 堆叠交互为RNA分子提供了额外的稳定性，因此它们对RNA分子的整体自由能有着重要的贡献。

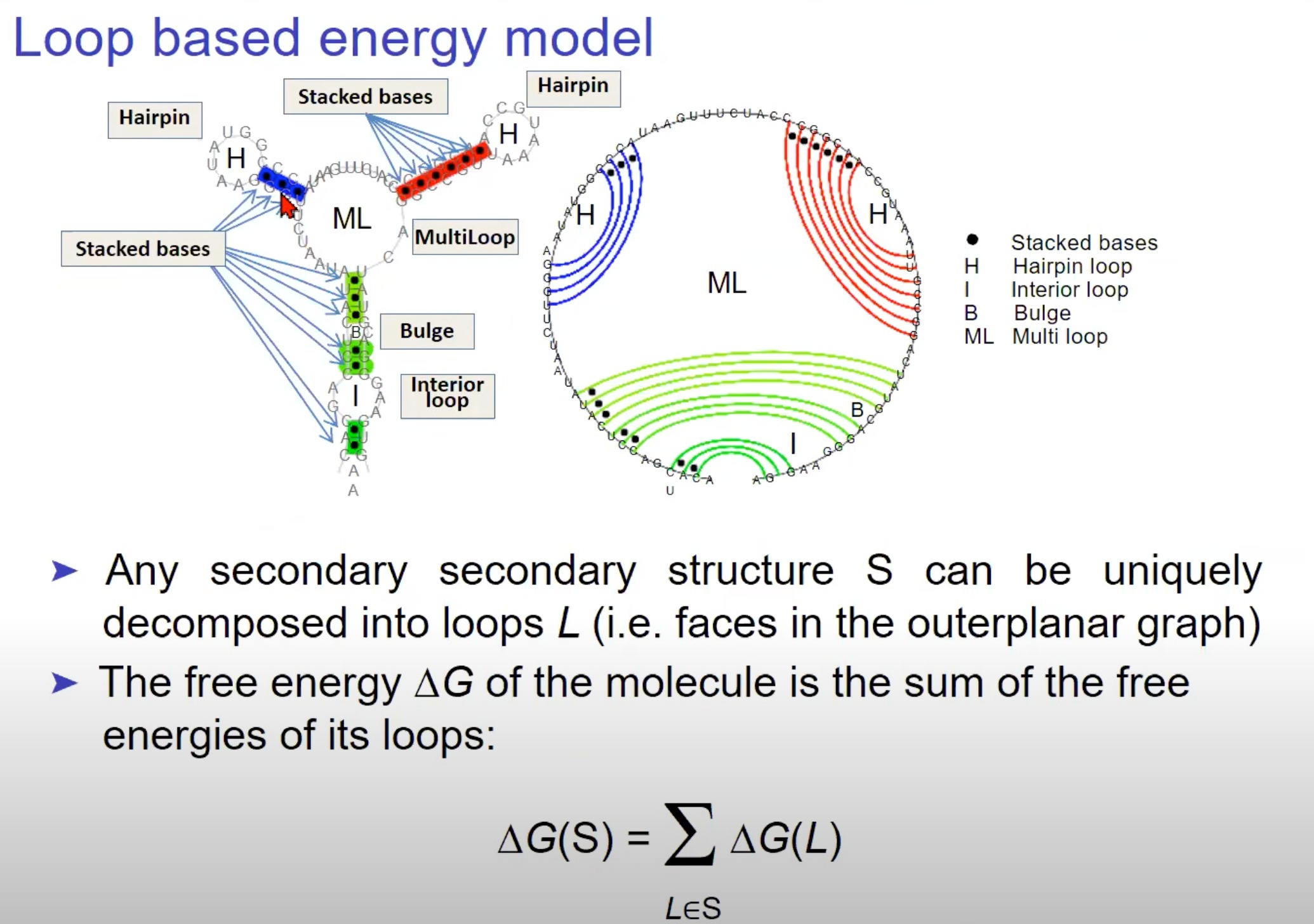
• 基于环（Loop)的能量模型

1. 堆叠的碱基（Stacked bases）、发夹环（Hairpin loop）、内部环（Interior loop）、Bulge、以及多环（Multi loop）。这些是RNA二级结构的基本组成部分。

“任何二级结构 ( S ) 都可以被唯一地分解成多个环 ( L )”：这意味着任何RNA的二级结构都可以被唯一地分解为环。

• “分子的自由能 ( $\Delta G $) 是其环的自由能之和”：整个RNA分子的自由能是由它的各个环的自由能组成的。
• 这可以用以下公式表示：
  $
  \Delta G(S) = \sum_{L \in S} \Delta G(L)
  $
  这表示分子 ( S ) 的自由能是它包含的所有环 ( L ) 的自由能的总和。

扩展补充：

• Structural ensemble and base-pairing probability

二维的点图，用于可视化RNA分子中可能的碱基配对的概率

在室温下，RNA不仅形成一个结构，而是存在为一系列可能的结构，称为集合(ensemble)

使用热力学理论来计算特定结构的概率

Stochastic context free grammars

上下文无关文法 (CFG)，用于生成回文：
V = { S } , T = { a , b } , P = { S → a S a , S → b S b , S → ϵ } V = \{S\}, \quad T = \{a, b\}, \quad P = \{S \rightarrow aSa, S \rightarrow bSb, S \rightarrow \epsilon\} V={S},T={a,b},P={S→aSa,S→bSb,S→ϵ}
这个CFG可以有效地描述字母表 ({a, b}) 上的所有回文。

RNA文法的例子。这是一个上下文无关文法，旨在模拟RNA的二级结构。RNA分子由四种碱基组成：A（腺苷）、C（鸟苷）、G（鸟嘌呤）和U（尿嘧啶）。
V = { S } , T = { a , c , g , u } , P = { S → a S u , S → c S g , … } V = \{S\}, \quad T = \{a, c, g, u\}, \quad P = \{S \rightarrow aSu, S \rightarrow cSg, \dots\} V={S},T={a,c,g,u},P={S→aSu,S→cSg,…}

这里的产生规则模拟了RNA的碱基配对，例如A与U配对，C与G配对。

解析树 (Parse Tree) 描述了如何使用给定的文法来派生特定的RNA序列。在这个例子中，给定的RNA序列是 (ACAGGAACUGUACGCUGCACCGC)，解析树展示了如何从初始非终结符 (S) 开始，通过多次应用产生规则来得到这个序列。

此外，RNA的二级结构图展示了该序列的配对模式，其中一些碱基通过氢键配对形成稳定的结构。