【算法挑战】设计一个支持增量操作的栈（含解析、源码）

1381.设计一个支持增量操作的栈

https://leetcode-cn.com/problems/design-a-stack-with-increment-operation/

1381.设计一个支持增量操作的栈
- 题目描述
- 方法 1: 用数组或链表模拟栈
  - 数组
  - 复杂度分析
  - 链表
  - 复杂度分析
  - 代码
- 方法 2: 空间换时间
  - 图解
  - 复杂度分析
  - 代码

题目描述

请你设计一个支持下述操作的栈。实现自定义栈类 CustomStack ：CustomStack(int maxSize)：用 maxSize 初始化对象，maxSize 是栈中最多能容纳的元素数量，栈在增长到 maxSize 之后则不支持 push 操作。
void push(int x)：如果栈还未增长到 maxSize ，就将 x 添加到栈顶。
int pop()：弹出栈顶元素，并返回栈顶的值，或栈为空时返回 -1 。
void inc(int k, int val)：栈底的 k 个元素的值都增加 val 。如果栈中元素总数小于 k ，则栈中的所有元素都增加 val 。示例：输入：
["CustomStack","push","push","pop","push","push","push","increment","increment","pop","pop","pop","pop"]
[[3],[1],[2],[],[2],[3],[4],[5,100],[2,100],[],[],[],[]]
输出：
[null,null,null,2,null,null,null,null,null,103,202,201,-1]
解释：
CustomStack customStack = new CustomStack(3); // 栈是空的 []
customStack.push(1);                          // 栈变为 [1]
customStack.push(2);                          // 栈变为 [1, 2]
customStack.pop();                            // 返回 2 --> 返回栈顶值 2，栈变为 [1]
customStack.push(2);                          // 栈变为 [1, 2]
customStack.push(3);                          // 栈变为 [1, 2, 3]
customStack.push(4);                          // 栈仍然是 [1, 2, 3]，不能添加其他元素使栈大小变为 4
customStack.increment(5, 100);                // 栈变为 [101, 102, 103]
customStack.increment(2, 100);                // 栈变为 [201, 202, 103]
customStack.pop();                            // 返回 103 --> 返回栈顶值 103，栈变为 [201, 202]
customStack.pop();                            // 返回 202 --> 返回栈顶值 202，栈变为 [201]
customStack.pop();                            // 返回 201 --> 返回栈顶值 201，栈变为 []
customStack.pop();                            // 返回 -1 --> 栈为空，返回 -1提示：1 <= maxSize <= 1000
1 <= x <= 1000
1 <= k <= 1000
0 <= val <= 100
每种方法 increment，push 以及 pop 分别最多调用 1000 次来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/design-a-stack-with-increment-operation
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

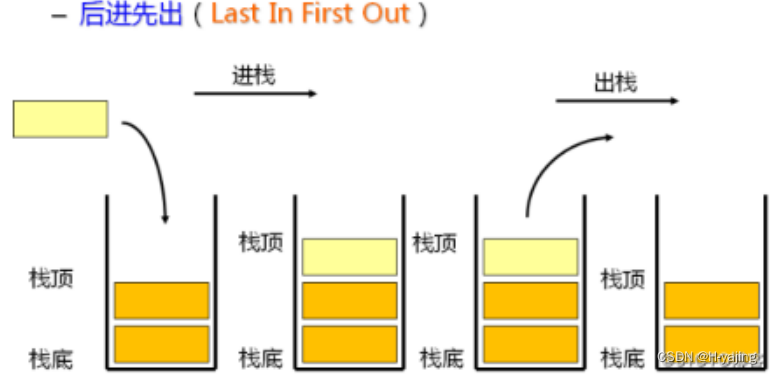
方法 1: 用数组或链表模拟栈

数组

使用数组来模拟栈，可以实现时间复杂度 $O (1)$ 的 push 和 pop，和 $O (k)$ 的 inc，剩下的就跟着题目描述来实现就好了。

当栈元素个数等于 maxSize 时不允许继续入栈；
当栈为空时，出栈操作返回 -1；
增量操作时，当栈元素多于 k 个，将栈底的 k 个元素都加 val，栈元素少于 k 个时将所有元素都加上 val。

复杂度分析

时间复杂度：push 和 pop 是 $O (1)$ ，inc 是 $O (k)$ 。
空间复杂度： $O (ma x S i ze)$ 。

链表

也可以使用链表来模拟栈，入栈出栈都只操作 head，也能实现时间复杂度 $O (1)$ 的 push 和 pop 操作，但 inc 操作的话，由于找到从链表尾端开始的第 k 个元素 (可以用双指针来找) 的时间复杂度是 $O (n)$ ，然后将链表尾端的 k 个元素进行增量操作的时间复杂度是 $O (k)$ ，所以增量操作总的时间复杂度是 $O (n + k)$ 。

复杂度分析

时间复杂度：push 和 pop 是 $O (1)$ ，inc 是 $O (n + k)$ 。
空间复杂度： $O (ma x S i ze)$ 。

代码

JavaScript Code

/*** @param {number} maxSize*/
var CustomStack = function (maxSize) {this.list = [];this.maxSize = maxSize;
};/*** @param {number} x* @return {void}*/
CustomStack.prototype.push = function (x) {if (this.list.length < this.maxSize) {this.list.push(x);}
};/*** @return {number}*/
CustomStack.prototype.pop = function () {const item = this.list.pop();return item === void 0 ? -1 : item;
};/*** @param {number} k* @param {number} val* @return {void}*/
CustomStack.prototype.increment = function (k, val) {for (let i = 0; i < k && i < this.list.length; i++) {this.list[i] += val;}
};/*** Your CustomStack object will be instantiated and called as such:* var obj = new CustomStack(maxSize)* obj.push(x)* var param_2 = obj.pop()* obj.increment(k,val)*/

Python Code

class CustomStack(object):def __init__(self, maxSize):""":type maxSize: int"""self.list = []self.maxSize = maxSizedef size(self):return len(self.list)def push(self, x):""":type x: int:rtype: None"""if self.size() < self.maxSize:self.list.append(x)def pop(self):""":rtype: int"""return -1 if self.size() == 0 else self.list.pop()def increment(self, k, val):""":type k: int:type val: int:rtype: None"""size = k if k < self.size() else self.size()for i in range(0, size):self.list[i] += val# Your CustomStack object will be instantiated and called as such:
# obj = CustomStack(maxSize)
# obj.push(x)
# param_2 = obj.pop()
# obj.increment(k,val)

方法 2: 空间换时间

其实我们只在出栈时才关心元素的值，所以在增量操作的时候，可以不用去更新栈内的元素，而是用一个 hashMap 来记录第几个元素需要增加多少。出栈时，检查当前元素的下标是否在 hashMap 中有记录，有的话就加上增量再出栈。这样我们就得到了时间复杂度 $O (1)$ 的增量操作，不过代价就是额外的 $O (N)$ 空间。

图解

在这里插入图片描述

复杂度分析

时间复杂度：push, pop 和 inc 都是 $O (1)$ 。
空间复杂度： $O (ma x S i ze)$ ，模拟栈的数组和哈希表的空间都是 $O (ma x S i ze)$ 。

代码

JavaScript Code

/*** @param {number} maxSize*/
var CustomStack = function (maxSize) {this.list = [];this.maxSize = maxSize;this.hashMap = {};
};/*** @param {number} key* @param {number} value* @return {void}*/
CustomStack.prototype._setInc = function (key, value) {if (!(key in this.hashMap)) {this.hashMap[key] = 0;}this.hashMap[key] += value;
};/*** @param {number} key* @return {number}*/
CustomStack.prototype._getInc = function (key) {return this.hashMap[key] || 0;
};/*** @return {number}*/
CustomStack.prototype._size = function () {return this.list.length;
};/*** @param {number} x* @return {void}*/
CustomStack.prototype.push = function (x) {if (this._size() < this.maxSize) {this.list.push(x);}
};/*** @return {number}*/
CustomStack.prototype.pop = function () {const top = this._size() - 1;const inc = this._getInc(top);let item = this.list.pop();if (item === void 0) {return -1;}item += inc;const newTop = top - 1;this._setInc(newTop, inc);this.hashMap[top] = 0;return item;
};/*** @param {number} k* @param {number} val* @return {void}*/
CustomStack.prototype.increment = function (k, val) {const size = this._size();k = k < size ? k - 1 : size - 1;this._setInc(k, val);
};/*** Your CustomStack object will be instantiated and called as such:* var obj = new CustomStack(maxSize)* obj.push(x)* var param_2 = obj.pop()* obj.increment(k,val)*/