1. 红黑树的概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

最短路径：全黑；最长路径：一黑一红交替。

由于avl树要求严格的平衡，因此相比于红黑树来说需要更频繁的旋转来保证平衡，所以整体而言效率是比红黑树要低一点。

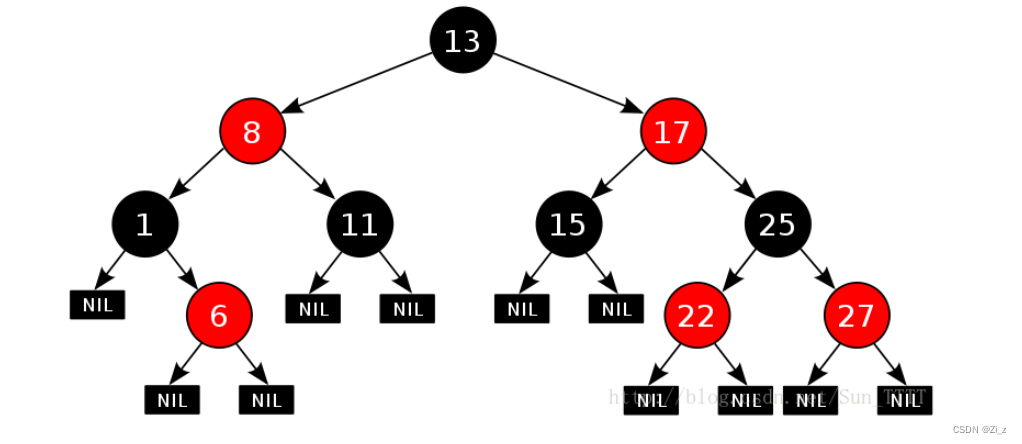
2. 红黑树的性质

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点必须是黑色的，保证没有任何一条路径会出现连续的红节点
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

3. 结点的定义

//枚举颜色
enum Color {RED,BLACK
};template<class K, class V>
struct RBTreeNode {RBTreeNode(const pair<const K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){ }pair<const K, V> _kv;//需要再增加一个结点颜色信息Color _col;RBTreeNode<const K, V>* _left;RBTreeNode<const K, V>* _right;//同样是需要父亲结点，后续调整旋转需要找到父亲RBTreeNode<const K, V>* _parent;
};

4. 结点的插入

往已经是满足红黑树性质的树中插入一个结点时，待插入结点的颜色一定要设置为红色，为什么？

若插入一个黑色结点，那么必然会违反性质4，若插入红色节点则不一定会违反性质3。

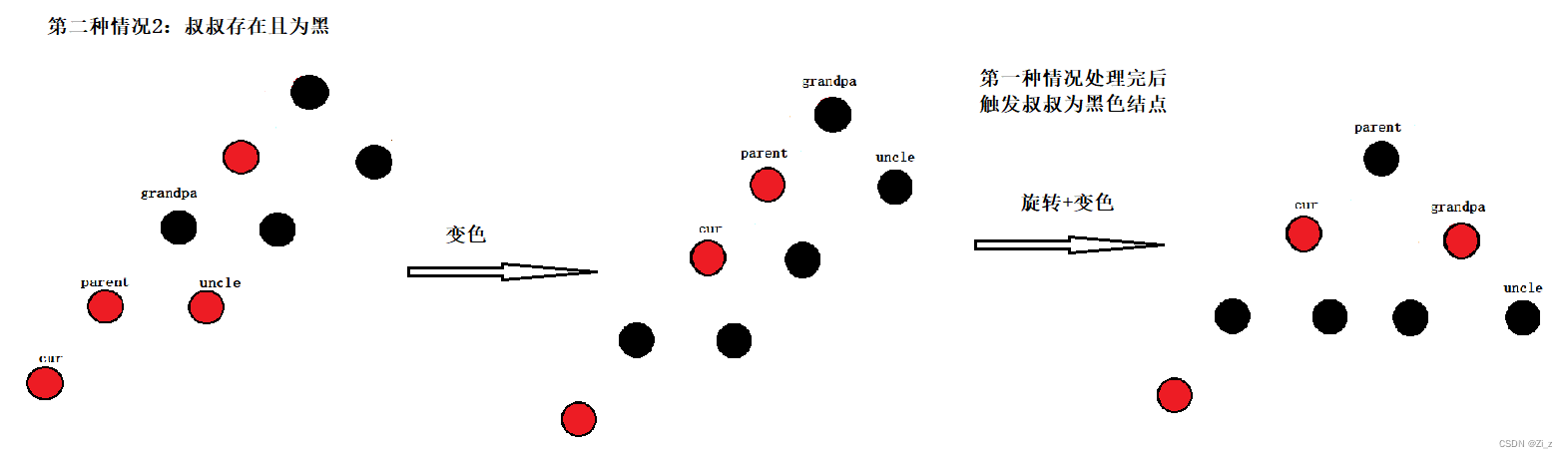
红黑树插入的关键在于要看叔叔结点的颜色，具体情况可分为两种：

1. 叔叔存在且为红
   
2. 叔叔不存在或者叔叔存在且为黑
   
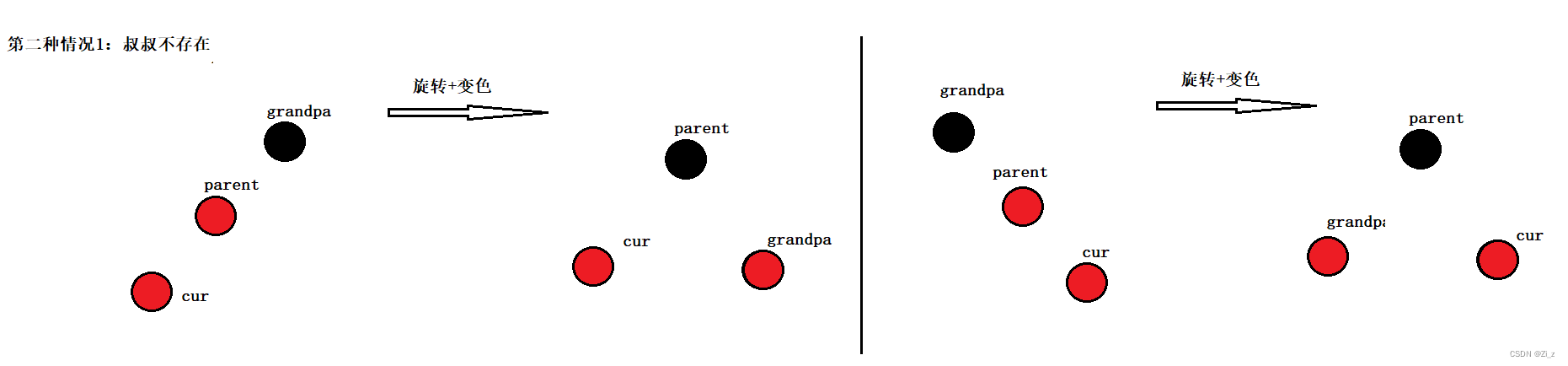
   叔叔存在且为黑是第一种情况触发后才会出现：
   

5. 整体代码

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O($lo{g}_{2}N$)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

#pragma once
#include <iostream>using namespace std;enum Color {RED,BLACK
};template<class K, class V>
struct RBTreeNode {RBTreeNode(const pair<const K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}pair<const K, V> _kv;enum Color _col;RBTreeNode<const K, V>* _left;RBTreeNode<const K, V>* _right;RBTreeNode<const K, V>* _parent;
};template<class K, class V>
class RBTree {typedef RBTreeNode<const K, V> Node;
public:bool insert(const pair<const K, V>& kv) {if (!_root) {_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur) {if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first) {parent->_right = cur;}else {parent->_left = cur;}cur->_parent = parent;//parent为红需要一直往上调整while (parent && parent->_col == RED) {Node* grandpa = parent->_parent;if (grandpa->_left == parent) {Node* uncle = grandpa->_right;//叔叔存在且为红if (uncle && uncle->_col == RED) {//把父亲和叔叔染黑//爷爷染红继续往上调整parent->_col = uncle->_col = BLACK;grandpa->_col = RED;cur = grandpa;parent = cur->_parent;}//叔叔不存在或者存在且为黑else {//单纯的一边高(直线)单旋if (cur == parent->_left) {rotateRight(grandpa);parent->_col = BLACK;cur->_col = grandpa->_col = RED;}//折线情况需要双旋else {rotateLeft(parent);rotateRight(grandpa);cur->_col = BLACK;parent->_col = grandpa->_col = RED;}break;}}//同样的逻辑else {Node* uncle = grandpa->_left;if (uncle && uncle->_col == RED) {parent->_col = uncle->_col = BLACK;grandpa->_col = RED;cur = grandpa;parent = cur->_parent;}else {if (parent->_right == cur) {rotateLeft(grandpa);grandpa->_col = cur->_col = RED;parent->_col = BLACK;}else {rotateRight(parent);rotateLeft(grandpa);parent->_col = grandpa->_col = RED;cur->_col = BLACK;}break;}		 }}_root->_col = BLACK;return true;}bool isBlance() {if (_root->_col != BLACK) {return false;}int cnt = 0;Node* cur = _root;while (cur) {cnt += cur->_col == BLACK;cur = cur->_left;}return _isBlance(_root, 0, cnt);}int getHeight() {return getHeight(_root);}private:int getHeight(Node* root) {if (!root) {return 0;}int leftH = getHeight(root->_left);int rightH = getHeight(root->_right);return max(leftH, rightH) + 1;}bool _isBlance(Node* root, int blackcnt, int t) {if (!root) {cout << blackcnt << ' ' << t << endl;return t == blackcnt;}if (root->_col == RED && root->_parent && root->_parent->_col == RED) {return false;}return _isBlance(root->_left, blackcnt + (root->_col == BLACK), t) && _isBlance(root->_right, blackcnt + (root->_col == BLACK), t);}void rotateLeft(Node* parent) {Node* cur = parent->_right;Node* curleft = cur->_left;if (curleft) {curleft->_parent = parent;}parent->_right = curleft;cur->_left = parent;Node* oldparent = parent->_parent;parent->_parent = cur;cur->_parent = oldparent;if (!oldparent) {_root = cur;}else {if (oldparent->_left == parent) {oldparent->_left = cur;}else {oldparent->_right = cur;}}}void rotateRight(Node* parent) {Node* cur = parent->_left;Node* curright = cur->_right;if (curright) {curright->_parent = parent;}parent->_left = curright;cur->_right = parent;Node* oldparent = parent->_parent;parent->_parent = cur;cur->_parent = oldparent;if (!oldparent) {_root = cur;}else {if (oldparent->_left == parent) {oldparent->_left = cur;}else {oldparent->_right = cur;}}}private:Node* _root = nullptr;
};