04 相机与图像
4.1 相机模型
4.1.1 针孔相机模型
针孔模型描述了一束光线通过针孔后,在针孔背面投影成像的关系(类似小孔成像原理)。
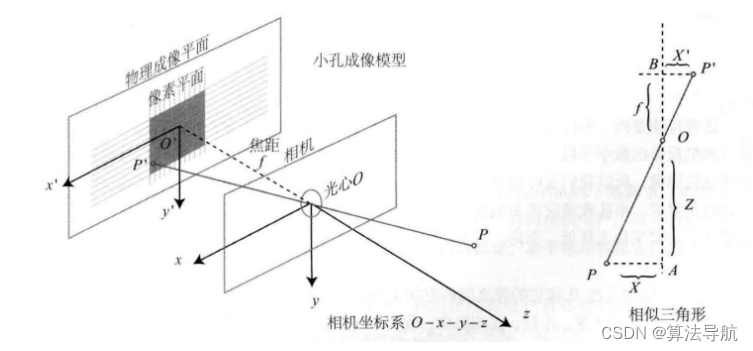
根据相似三角关系
Z f = − X X ′ = − Y Y ′ (3-1) \frac{Z}{f}=-\frac{X}{X^{\prime}}=-\frac{Y}{Y^{\prime}} \tag{3-1} fZ=−X′X=−Y′Y(3-1)
其中,负号表示成的像是倒立的。
但实际相机得到的图像并不是倒像,我们等价地将成像平面对称地放到相机前方,这样就可以把负号去掉,
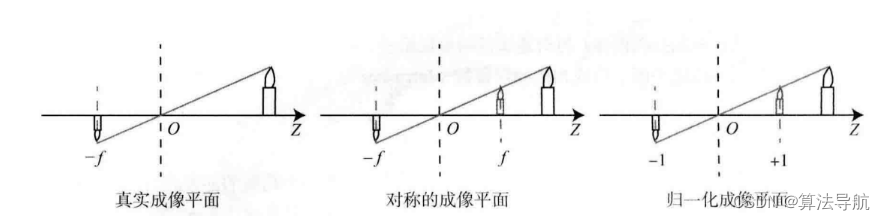
Z f = X X ′ = Y Y ′ (3-2) \frac{Z}{f}=\frac{X}{X^{\prime}}=\frac{Y}{Y^{\prime}} \tag{3-2} fZ=X′X=Y′Y(3-2)
整理得
{ X ′ = f X Z Y ′ = f Y Z (3-3) \left\{\begin{array}{l} {X^{\prime}}=f\frac{X}{Z} \\ \\ {Y^{\prime}}=f\frac{Y}{Z} \end{array}\right. \tag{3-3} ⎩ ⎨ ⎧X′=fZXY′=fZY(3-3)
像素坐标与成像平面之间,相差了一个缩放和一个原点的平移。假设像素坐标在 u u u 轴上缩放了 α \alpha α 倍, 在 v v v 轴上缩放了 β \beta β 倍,同时,原点平移了 [ c x , c y ] T [c_x, c_y]^T [cx,cy]T。那么, P ′ P' P′ 在成像平面坐标系和像素坐标系之间的关系为:
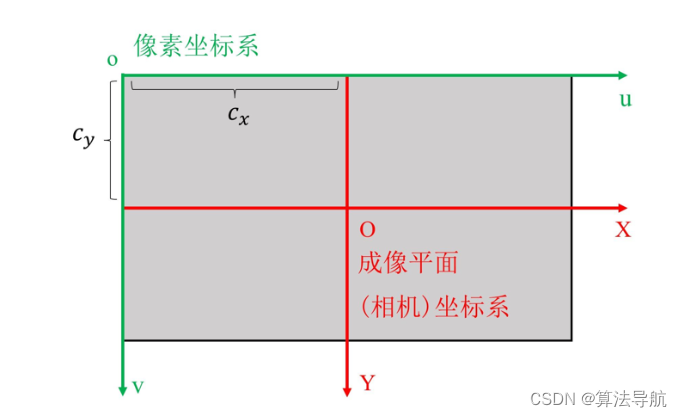
{ u = α X ′ + c x v = β Y ′ + c y (3-4) \left\{\begin{array}{l} u=\alpha X^{\prime}+c_{x} \\ v=\beta Y^{\prime}+c_{y} \end{array}\right. \tag{3-4} {u=αX′+cxv=βY′+cy(3-4)
代入式(3-3),得
{ u = α f X Z + c x v = β f Y Z + c y (3-5) \left\{\begin{array}{l} u=\alpha f \frac{X}{Z}+c_{x} \\ \\ v=\beta f \frac{Y}{Z}+c_{y} \end{array}\right. \tag{3-5} ⎩ ⎨ ⎧u=αfZX+cxv=βfZY+cy(3-5)
记 α f = f x , \alpha f=f_x, αf=fx,, β f = f y \beta f=f_y βf=fy 得
{ u = f x X Z + c x v = f y Y Z + c y (3-6) \left\{\begin{array}{l} u=f_{x} \frac{X}{Z}+c_{x} \\ \\ v=f_{y} \frac{Y}{Z}+c_{y} \end{array}\right. \tag{3-6} ⎩ ⎨ ⎧u=fxZX+cxv=fyZY+cy(3-6)
写成矩阵形式
[ u v 1 ] = 1 Z [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] = def 1 Z K P (3-7) \left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\frac{1}{Z}\left[\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right] \stackrel{\text { def }}{=} \frac{1}{Z} \boldsymbol{K} \boldsymbol{P} \tag{3-7} uv1 =Z1 fx000fy0cxcy1 XYZ = def Z1KP(3-7)
将 Z Z Z 移到左边
Z [ u v 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] = def K P (3-8) Z\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right] \stackrel{\text { def }}{=} \boldsymbol{K} \boldsymbol{P} \tag{3-8} Z uv1 = fx000fy0cxcy1 XYZ = def KP(3-8)
中间的矩阵称为相机内参数,一般在相机出厂后便已确定。
由于相机在运动,点 P P P 的相机坐标应由他的世界坐标( P w P_w Pw)根据相机当前位姿变换得到
Z P u v = Z [ u v 1 ] = K P = K ( R P w + t ) = K T P w (3-9) Z \boldsymbol{P}_{u v}=Z\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\boldsymbol{K} \boldsymbol{P}=\boldsymbol{K}\left(\boldsymbol{R} \boldsymbol{P}_{\mathrm{w}}+\boldsymbol{t}\right)=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}_{\mathrm{w}} \tag{3-9} ZPuv=Z uv1 =KP=K(RPw+t)=KTPw(3-9)
其中, R \boldsymbol{R} R、 t \boldsymbol{t} t 为外参。
上式描述了从世界坐标系到相机坐标系再到像素坐标系的过程。
将世界坐标转换到相机坐标后,再除掉最后一维的数值,这相当于把最后一维作归一化处理,得到它在归一化平面上的投影:
( R P w + t ) = [ X , Y , Z ] T ⏟ 相机坐标 → [ X / Z , Y / Z , 1 ] T ⏟ 归一化坐标 \left(\boldsymbol{R} \boldsymbol{P}_{\mathrm{w}}+\boldsymbol{t}\right)=\underbrace{[X, Y, Z]^{\mathrm{T}}}_{\text {相机坐标 }} \rightarrow \underbrace{[X / Z, Y / Z, 1]^{\mathrm{T}}}_{\text {归一化坐标 }} (RPw+t)=相机坐标 [X,Y,Z]T→归一化坐标 [X/Z,Y/Z,1]T
可知,点的深度信息在投影过程中丢失了(变成二维),所以单目视觉无法得到像素点深度值。
4.1.2 畸变模型
(1)由透镜形状引起的畸变称为径向畸变,一般有桶形畸变和枕形畸变两类。
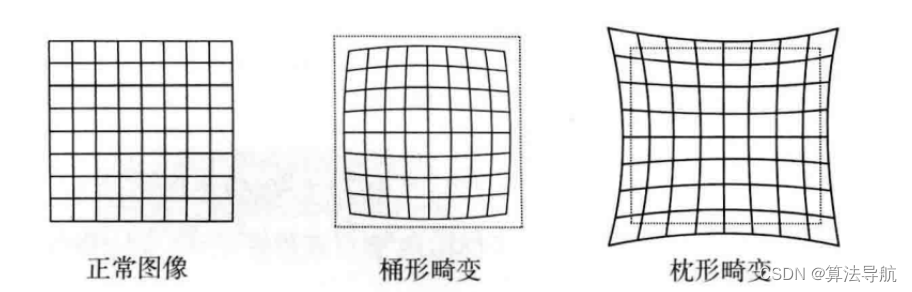
对于径向畸变,离中心距离越远,畸变越严重;穿过图像中心和光轴有交点的直线形状不变。
(2)在相机组装过程中,透镜和成像平面无法完全平行,会产生切向畸变。
(3)下面用数学模型进行描述:假设归一化平面上存在一点 P P P,坐标为 [ x , y ] T [x, y]^T [x,y]T,极坐标为 [ r , θ ] T [r, \theta]^T [r,θ]T,那么,正常归一化平面坐标和畸变后的坐标之间的关系为
{ x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) (3-10) \left\{\begin{array}{l} x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)\\ \\ y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6) \end{array}\right. \tag{3-10} ⎩ ⎨ ⎧xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6)(3-10)
类似的,切向畸变数学模型为
{ x distorted = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y distorted = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y (3-11) \left\{\begin{array}{l} \begin{aligned} &x_{\text {distorted }}=x+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right) \\ &y_{\text {distorted }}=y+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x y \end{aligned} \end{array}\right. \tag{3-11} {xdistorted =x+2p1xy+p2(r2+2x2)ydistorted =y+p1(r2+2y2)+2p2xy(3-11)
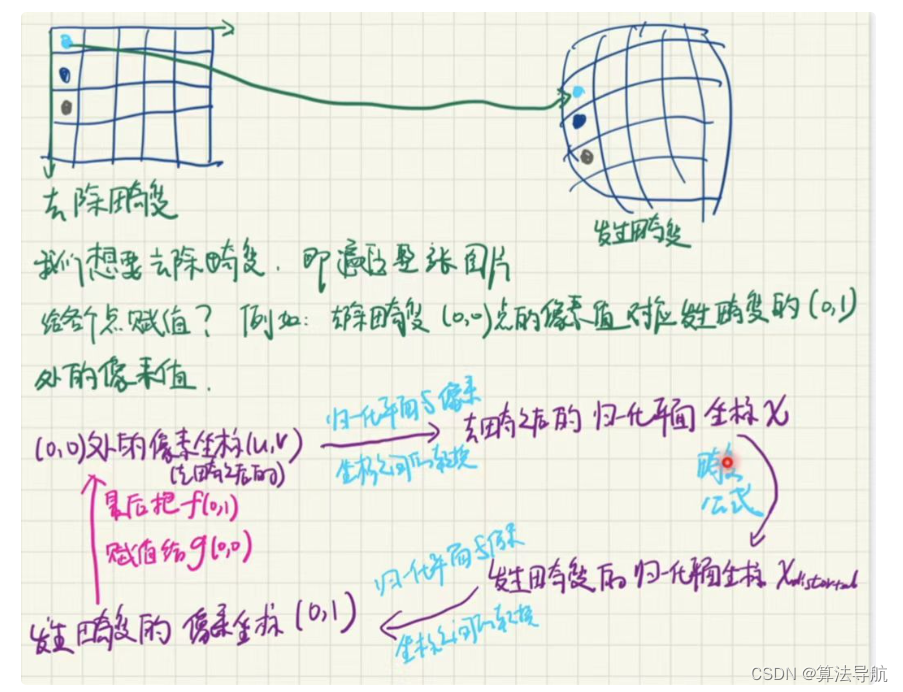
(4)去畸变的过程:
-
将三维空间上的点投影到归一化平面,得到坐标 [ x , y ] T [x, y]^T [x,y]T;
-
计算径向畸变和切向畸变
{ x d i s t o r t e d = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t o r t e d = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y (3-12) \left\{\begin{array}{l} x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right)\\ \\ y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x y \end{array}\right. \tag{3-12} ⎩ ⎨ ⎧xdistorted=x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)ydistorted=y(1+k1r2+k2r4+k3r6)+p1(r2+2y2)+2p2xy(3-12)
- 通过内参矩阵将相机坐标投影到像素平面。
(5)单目相机的成像过程
-
世界坐标系下一点 P w P_w Pw;
-
经旋转平移得到相机坐标 P ~ c = R P w + t \tilde{P}_{\mathrm{c}}=\boldsymbol{RP_w+t} P~c=RPw+t;
-
将坐标的三个分量分别除以 Z Z Z,得到归一化坐标 P c = [ X / Z , Y / Z , 1 ] T P_c=[X/Z, Y/Z, 1]^T Pc=[X/Z,Y/Z,1]T;
-
计算发生畸变后的坐标;
-
经过内参矩阵,得到像素坐标 P u v = K P c \boldsymbol{P}_{uv}=\boldsymbol{KP_c} Puv=KPc。
4.1.3 双目相机模型
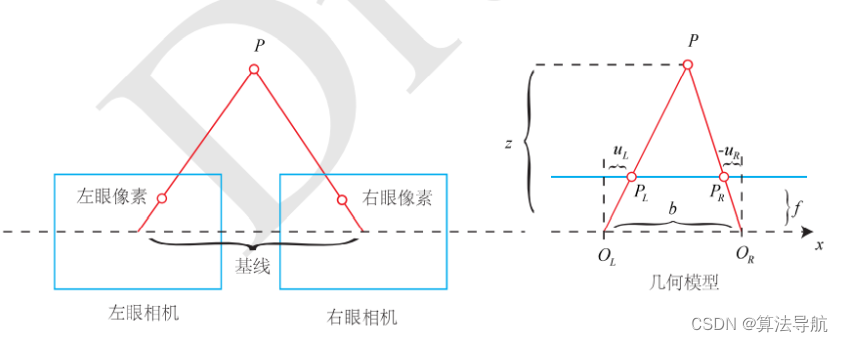
其中, O L O_L OL 和 O R O_R OR为左右相机光圈中心,两者之间的距离称为基线; f f f 为焦距; u R u_R uR 为负数,需加负号。
根据几何关系,有
z − f z = b − ( u L − u R ) b = b − u L + u R b (3-13) \frac {z-f}{z}=\frac {b-(u_L-u_R)} {b}=\frac {b-u_L+u_R} {b} \tag{3-13} zz−f=bb−(uL−uR)=bb−uL+uR(3-13)
定义 d = u L − u R d=u_L-u_R d=uL−uR,称为视差, 整理上式得,
z = f b d (3-14) z=\frac {fb}{d} \tag{3-14} z=dfb(3-14)
可见,视差越大,距离越近。基线 b b b 越大,可测量的距离就越大;反之,小型双目器件只能测量很近的距离。
4.1.4 RGB-D 相机模型
RGB-D 相机可以主动测量每个像素的深度,按原理可分为两类:
-
通过红外结构光原理测量像素距离。
-
通过飞行时间原理测量像素距离。
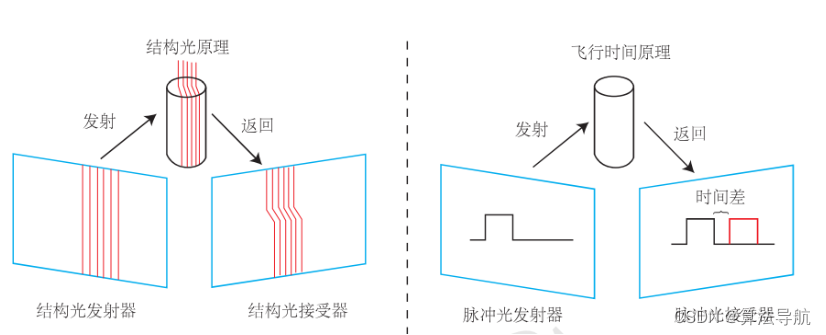
RGB-D 相机容易受到日光或其他传感器的干扰,因此不能在室外使用。
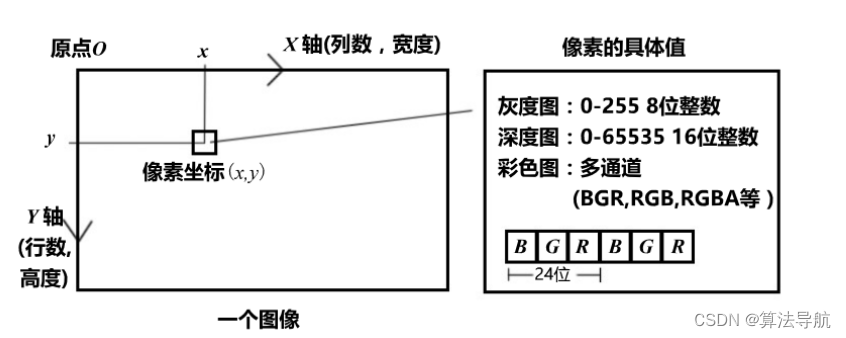
4.2 图像