[PyTorch][chapter 62][强化学习-基本概念]

前言：

强化学习概念
马尔科夫决策
Bellman 方程
格子世界例子

一强化学习

强化学习必须在尝试之后，才能发现哪些行为会导致奖励的最大化。
当前的行为可能不仅仅会影响即时奖赏，还有影响下一步奖赏和所有奖赏

强化学习五要素如下：

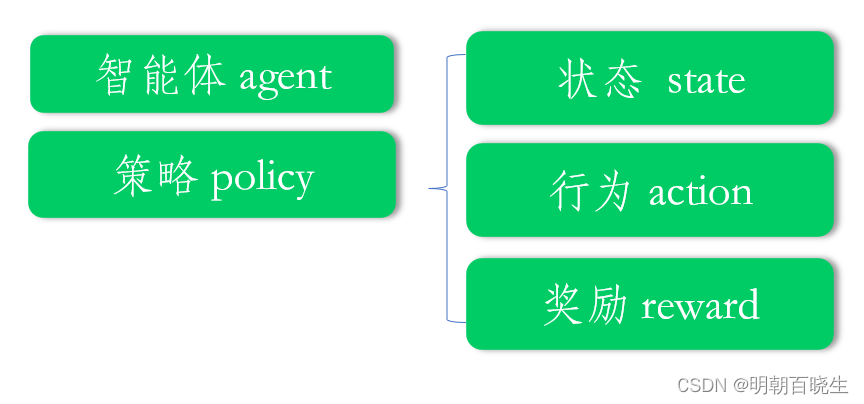
1.2 强化学习流程

1：产生轨迹(trajectory）

2：策略评估(policy-evaluate)

3：策略提升（policy-improve）

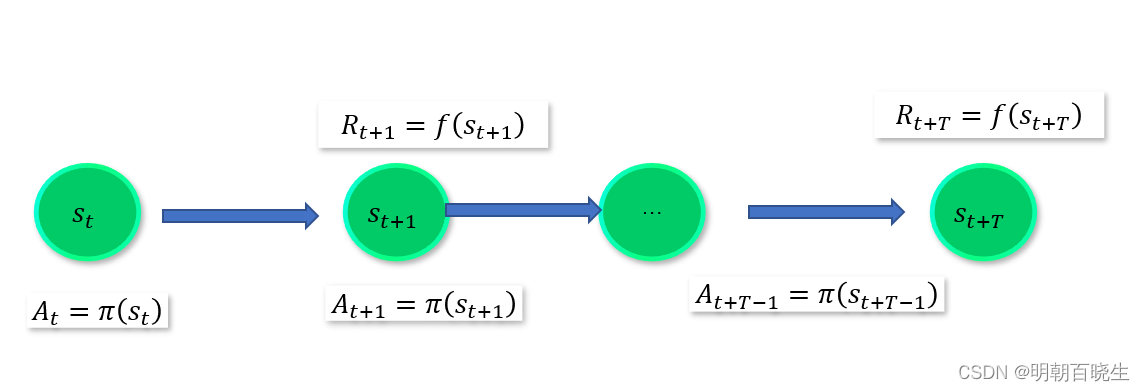
这里重点讲一下产生轨迹：

当前处于某个state 下面，

按照策略选择 action = $A_t= \pi(s_t)$

根据新的state 给出 reward: $R_{t+1}=f(s_{t+1})$

最后产生了轨迹链

二马尔科夫决策

2.1 马尔科夫决策要求：

   1：能够检测到理想的状态
   2：可以多次尝试
   3：系统的下个状态只与当前信息有关，与更早的状态无关。
决策过程中还可和当前采取的动作有关.

2.2 马尔科夫决策五要素

S: 状态集合 states
A: 动作集合 actions
P: 状态转移概率 $P_{S_t \to s_{t+1}}^a$
R: 奖励函数（reward function) ，agent 采取某个动作后的及时奖励
r: 折扣系数意味当下的reward 比未来反馈更重要

$\sum_{t=0}^{\infty }r^t R(s_t)$

$r \in (0,1]$

2.3 主要流程

1: Agent 处于状态 $s_0$

2: 按照策略选择动作 $a_0$

3：执行该动作后,有一定的概率转移到新的状态 $p_{s_0\rightarrow s_1}^a$

2.4 价值函数

$V(s)=E_{\pi}(\sum_{t=1}^{T} r_t|S_0=s)$

当前时刻处于状态s,未来获得期望的累积奖赏

分为两种： state 价值函数 state-action 价值函数

最优价值函数：

不同策略下, 累积奖赏最大的 $v_{*}=max_{\pi}v_{\pi}(x)$

2.5 策略 policy

当前状态s 下,按照策略,要采用的动作

$action=\pi(s)$

三 Bellman 方程

4.1 状态值函数为：

$V_{T}^{\pi}(x)=E_{\pi}[\frac{1}{T}\sum_{t=1}^Tr_t|x_0=x]$ : T 步累积奖赏

$V_{\gamma}^{T}(x)=E_{\pi}[\frac{1}{T}\sum_{t=0}^T \gamma^tr_{t+1}|x_0=x]$ : $\gamma$ 折扣累积奖赏， $\gamma \in (0,1]$

4.2 Bellman 方程

$V_{T}^{\pi}(x)=$ $=\sum_{a \in A}\pi (x,a) \sum_{x^{'} \in X} P_{x\rightarrow x^{'}}^a(\frac{1}{T} R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}V_{T-1}^{\pi}(x^{'}))$

证明：

$V_{T}^{\pi}(x)=E_{\pi}[\frac{1}{T}\sum_{t=1}^T r_t|x_0=x]$

$=E_{\pi}[\frac{1}{T}r_1+\frac{T-1}{T}\frac{1}{T-1}\sum_{t=2}^T r_t|x_0=x]$

$=\sum_{a \in A} \pi(x,a) \sum _{x^{'} \in X}P_{x\rightarrow x^{'}}^a (\frac{1}{T}R_{x\rightarrow x^{'}}^{a}+\frac{T-1}{T}E_{\pi}[\frac{1}{T-1}\sum_{t=1}^{T-1}r_t|x_0=x^{'}])$

$=\sum_{a \in A}\pi (x,a) \sum_{x^{'} \in X} P_{x\rightarrow x^{'}}^a(\frac{1}{T} R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}V_{T-1}^{\pi}(x^{'}))$

r折扣奖赏bellman 方程

$V_{\gamma}^{\pi}(x)=\sum_{a \in A}\sum_{x^{'} \in X} P_{x\rightarrow x^{'}}^a(R_{x\rightarrow x^{'}}^a+\gamma V_{r}^{\pi}(x'))$

四格子世界例子

在某个格子,执行上下左右步骤,其中步骤最短的

为最优路径

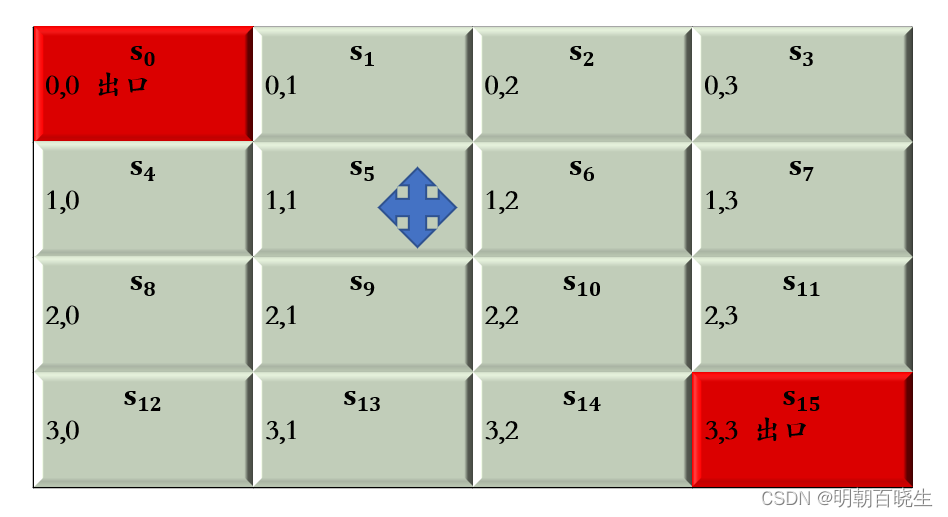
5.1：gridword.py

import numpy as np#手动输入格子的大小
WORLD_SIZE = 4
START_POS = [0,0]
END_POS = [WORLD_SIZE-1, WORLD_SIZE-1]
prob = 1.0
#折扣因子
DISCOUNT = 0.9
# 动作集={上,下,左,右}
ACTIONS = [np.array([0, -1]),    #leftnp.array([-1, 0]),  # upnp.array([0, 1]),   # rightnp.array([1, 0])]   # downclass GridwordEnv():def action_name(self, action):if action ==0:name = "左"elif action ==1:name = "上"elif action ==2:name = "右"else:name = "上"return namedef __init__(self):self.nA = 4 #action：上下左右self.nS = 16 #state: 16个状态self.S = []for i in range(WORLD_SIZE):for j in range(WORLD_SIZE):state =[i,j]self.S.append(state)def step(self, s, a):action = ACTIONS[a]state = self.S[s]done = Falsereward = 0.0next_state = (np.array(state) + action).tolist()if (next_state == START_POS) or (state == START_POS):next_state =  START_POSdone = Trueelif (next_state == END_POS) or (state == START_POS):next_state =  END_POSdone = Trueelse:x, y = next_state# 判断是否出界if x < 0 or x >= WORLD_SIZE or y < 0 or y >= WORLD_SIZE:reward = -1.0next_state = stateelse:reward = -1.0return prob, next_state, reward,done

5.2 main.py

# -*- coding: utf-8 -*-
"""
Created on Mon Nov 13 09:39:37 2023@author: chengxf2
"""import numpy as npdef init_state(WORLD_SIZE):S =[]for i in range(WORLD_SIZE):for j in range(WORLD_SIZE):state =[i,j]S.append(state) print(S)# -*- coding: utf-8 -*-
"""
Created on Fri Nov 10 16:48:16 2023@author: chengxf2
"""import numpy as np
import sys
from gym.envs.toy_text import discrete  #环境
from enum import Enum
from gridworld import GridwordEnvclass Agent():def __init__(self,env):self.discount_factor = 1.0 #折扣率self.theta = 1e-3 #最大偏差self.S = []self.env = env#当前处于的位置,V 累积奖赏def one_step_lookahead(self,s, v):R = np.zeros((env.nA)) #不同action的累积奖赏for action in range(env.nA):prob, next_state,reward, done = env.step(s, action) #只有一个next_state_index = self.env.S.index(next_state)#print("\n state",s ,"\t action ",action, "\t new_state ", next_state,"\t next_state_index ", next_state_index,"\t r: ",reward)r=  prob*(reward + self.discount_factor*v[next_state_index])R[action] +=r#print("\n state ",s, "\t",R)        return Rdef value_iteration(self, env, theta= 1e-3, discount_factor =1.0):v = np.zeros((env.nS)) #不同状态下面的累积奖赏,16个状态iterNum = 0while True:delta = 0.0for s in range(env.nS):R = self.one_step_lookahead(s,v)#在4个方向上面得到的累积奖赏best_action_value = np.max(R)#print("\n state ",s, "\t R ",R, "\t best_action_value ",best_action_value)bias = max(delta, np.abs(best_action_value-v[s]))v[s] =best_action_value#if (s+1)%4 == 0:#print("\n -----s ------------",s)iterNum +=1if bias<theta:breakprint("\n 迭代次数 ",iterNum)return vdef learn(self):policy = np.zeros((env.nS,env.nA))v = self.value_iteration(self.env, self.theta, self.discount_factor)for s in range(env.nS):R =  self.one_step_lookahead(s,v)best_action=  np.argmax(R)#print(s,best_action_value )policy[s,best_action] = 1.0return policy,vif __name__ == "__main__":env = GridwordEnv()agent =Agent(env)policy ,v = agent.learn()for s in range(env.nS):action = np.argmax(policy[s])act_name = env.action_name(action)print("\n state ",s, "\t action ",act_name, "\t 累积奖赏 ",v[s])

参考：

【强化学习玩游戏】1小时竟然就学会了强化学习dqn算法原理及实战（人工智能自动驾驶/深度强化学习/强化学习算法/强化学习入门/多智能体强化学习）_哔哩哔哩_bilibili

2-强化学习基本概念_哔哩哔哩_bilibili

3-马尔科夫决策过程_哔哩哔哩_bilibili

4-Bellman方程_哔哩哔哩_bilibili

5-值迭代求解_哔哩哔哩_bilibili

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/191411.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！