Java LeetCode篇-深入了解二叉树经典解法（三种方式实现：获取二叉树的最大深度）

🔥博客主页： 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍  

文章目录

        1.0 对称二叉树

        1.1 判断对称二叉树实现思路

        1.2 代码实现：判断对称二叉树

        2.0 二叉树的最大深度

        2.1 使用递归实现获取二叉树的最大深度思路

        2.2 代码实现：使用递归实现获取二叉树的最大深度

        2.3 使用非递归实现获取二叉树的最大深度思路

        2.4 代码实现：使用非递归实现获取二叉树的最大深度

        2.5 使用层序遍历实现获取二叉树的最大深度

        2.6 代码实现：使用层序遍历实现获取二叉树的最大深度

        3.0 二叉树的最小深度

        3.1 使用递归实现获取二叉树的最小深度思路

        3.2 代码实现：使用递归实现获取二叉树最小深度

        3.3 使用层序遍历实现获取二叉树的最小深度思路

        3.4 代码实现：使用层序遍历实现获取二叉树的最小深度

        4.0 翻转二叉树

        4.1 使用实现递归翻转二叉树思路

        4.2 代码实现：使用递归翻转二叉树

        5.0 二叉树经典解法的完整代码

        1.0 对称二叉树

题目：

        给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

OJ链接：

101. 对称二叉树

        1.1 判断对称二叉树实现思路

     假设该树的图：   

        具体思路为：如果当前节点的左子树的值等于当前节点的右子树时，可以说目前为止还是对称的，不能直接下结论，因为不能保证之后的节点是否对称。比如：当前节点的值为 1 ，它的左孩子的值为 2 ，它的右孩子的值为 2，此时可以说暂时是对称的，还需要接着向下判断。它的左孩子的左孩子的值为 3，它的右孩子的右孩子为 3 ，同理，现在还不能说明该树是否对称，当递归到底的时候，当前的节点的左右孩子都是 null ，此时可以返回 true ，不能足以证明该树对称，因为单单只是判断完外侧的节点，在外层回归的过程中，需要判断内层的节点是否对称，回归到节点值都为 2 的节点，接着进行内层递归，对于在外层判断完左孩子，那么接下来需要判断右孩子，同样，对于在外层判断完右孩子，那么接下来需要判断左孩子。如，刚刚的外层结束递出之后，开始回归，到节点为 2 的节点，对于左边的节点值为 2 的节点的右孩子，与右边的节点值为 2 的节点的左孩子进行比较，如果相同，由于说明不了什么，还得继续往下递出，直到该节点的左右孩子都为 null 时，可以返回 true 。最后返回到节点值为 1 的根节点中，可以得到该树是对称。

        在无论是外层递出还是内层递出：

         - 当左右孩子节点的值不相同的时候，就说明了该树时不相等的，直接返回 false ；

         - 遇到一个节点的左孩子不为 null 而右孩子为 null 时，可以直接返回 false ，不需要接着往后递出了。同理，遇到一个节点的右孩子不为 null ，而左孩子为 null 时，直接返回 false ；

         - 当且仅当，当该节点的左右孩子都为 null 时，返回 true ；

        1.2 代码实现：判断对称二叉树

    //判断对称二叉树public boolean isSymmetry(TreeNode root) {return isSymmetryRecursion(root.left,root.right);}private boolean isSymmetryRecursion(TreeNode left,TreeNode right) {if (left == null && right == null ) {return true;}if (left == null || right == null) {return false;}if (left.val != right.val) {return false;}return isSymmetryRecursion(left.left,right.right) && isSymmetryRecursion(left.right,right.left);}

        大体上的思路跟后序遍历二叉树一致。

        2.0 二叉树的最大深度

题目：

        给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

OJ链接：

104. 二叉树的最大深度

         2.1 使用递归实现获取二叉树的最大深度思路

        具体思路为：先从整体思路出发，得到最大的深度，无非就是比较左右子树的深度，选取较大的值 + 1，返回即可。当遇到的节点为 null 时，返回 0 ，结束递出。比如，节点值为 3 的节点，它的左子树的深度为 1，它的右子树的深度为 2 ,那么选取最大的值为 2 ，最后最大的值再加上 1 ，所以得出的该树的最大深度为 3 。

        接下来具体分析每一个节点：根节点值为 3 ，先获取左子树的深度：沿着该方向递出，直到遇到当前节点的左右孩子都为 null 时，返回 0 ，所以值为 9 的节点目前返回上一个递归调用的值为 1 ，对于根节点的左子树的深度为 1 ；再获取右子树的深度：沿着根节点的右子树递出，这次遇到的节点的左右子树都不为 null 时，对于当前值为 20 的节点来说，需要获取该左右子树的最大的值，先获取左子树的深度：沿着该方式递出，直到遇到的节点为 null 时，返回 0，节点值为 15 的节点的左右孩子都为 null ，返回 0 + 1 ，所以对于节点 20 来说，该左子树的深度为 1 ；接着继续来获取节点值为 20 的右子树的深度：沿着该方式递出，直到遇到的节点为 null 时，返回 0，节点值为 7 的左右孩子都为 null ，返回 0 + 1。那么选取较大的值 + 1，就是节点值为 20 的深度为 2 。相对与根节点来说已经得到了左右子树的深度了，分别为 1 与 2 ，选取最大的值 2 再加 1 就是该树的最大深度为 3 。

        2.2 代码实现：使用递归实现获取二叉树的最大深度

    //用递归方式求树的最大深度public int maximumDepthRecursion(TreeNode node) {if (node == null) {return 0;}int l = maximumDepth(node.left);int r = maximumDepth(node.right);return Math.max(l,r) + 1;}

        大体上思路跟后序遍历思路大致相同。

        2.3 使用非递归实现获取二叉树的最大深度思路

        具体思路为：在之前讲到使用非递归实现后序遍历的思路，跟这里的思路大致一致。简单再讲一下思路，根节点从左孩子开始出发，在到下一个节点之前，需要先把该节点压入栈中，直到 node == null 时，不再继续下去，按照原路返回。由于需要完成对右节点的操作后，需要返回该节点，所以不能直接把栈顶元素弹出，先查找栈顶元素，查看该右孩子是否为 null 或者已经完成对右孩子的相关操作之后，这才能弹出栈顶元素。如果以上情况都不符合，需要对右孩子进行处理。以上就是使用非递归实现后序循环，那么结合该题求树的最大深度，即什么时候栈的元素达到最大的时候，这时候就是树的最大深度。

        2.4 代码实现：使用非递归实现获取二叉树的最大深度

    //用非递归方式求树的最大深度public int maximumDepth(TreeNode root) {TreeNode curr = root;LinkedList<TreeNode> stack = new LinkedList<>();int max = 0;TreeNode pop = null;while (curr != null || !stack.isEmpty()) {if (curr != null) {stack.push(curr);curr = curr.left;if (max < stack.size()) {max = stack.size();}} else {TreeNode peek = stack.peek();if ( peek.right == null || peek.right == pop ) {pop = stack.pop();}else {curr = peek.right;}}}return max;}

        当然，这个时间复杂度比使用递归实现的要大，效率不如使用递归的实现二叉树最大深度。

        2.5 使用层序遍历实现获取二叉树的最大深度

        先了解层序遍历：顾名思义，按照层级进行依次访问节点。将每个节点压入队列中，按照先进先出的顺序依次访问队列中的节点。具体来说，我们从根节点开始，将根节点压入队列中，然后依次从队列中取出节点，将其左右子节点（如果存在）压入队列中。

        需要准备队列来存储节点，根据该数据结构的特性：先进先出，一开始先让根节点压入队列中，接着从队列中弹出来，如果弹出来的节点的左孩子不为 null 时，将其压入队列中；如果左孩子为 null 时，不需要压入队列中；同理，如果弹出来节点的右孩子不为 null 时，将其压入队列中。循环结束条件为：当队列中的元素个数为 0 时，退出循环。

        再结合该题的逻辑，该二叉树的最大深度就是树的层级数量。那么怎么才能得出 int depth 层级数量呢？再嵌套一个内层循环，每一层遍历结束之后，depth++ 。内层循环的次数为：当前的队列的元素的个数。

        2.6 代码实现：使用层序遍历实现获取二叉树的最大深度

    //使用层序遍历求树的最大深度public int sequenceMaxDepth(TreeNode root) {if (root == null) {return 0;}LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while ( !queue.isEmpty()) {int size = queue.size();for (int j = 0; j < size; j++) {TreeNode tp = queue.poll();if (tp.left != null) {queue.offer(tp.left);}if (tp.right != null) {queue.offer(tp.right);}//System.out.print(tp.val + " ");}//System.out.println();depth++;}return depth;}

        3.0 二叉树的最小深度

题目：

        给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

OJ链接：

111. 二叉树的最小深度

        二叉树的最小深度是指从根节点到最近叶子节点的最短路径上的节点数量。换句话说，最小深度是从根节点到最近的叶子节点的路径长度。

        3.1 使用递归实现获取二叉树的最小深度思路

        具体思路为：思路大体跟或去最大深度的思路差不太多，当比较前节点的左右子树，获取最小的值 + 1 ，则为当前节点的深度。获取最小深度相较于获取最大深度，多了一个判断条件，如果当前节点为 0 时，不应该参与比较。

如图例，该树的深度应该为 2 ，如果不加额外的条件来判断左右孩子节点是否为 null 时，那么此时根节点的右孩子为 null ，所以右子树为深度为 0 ；左孩子不为 null ，接着递归下去，直到 node == null 为止，从图可知，该根节点的左子树的深度为 1，因此用 1 与 0 来比较，获取最小的值为 0 ，再加上 1 ,最后结果为 1 。很明显不符合要求。所以，一定要加条件来判断，查看该节点的左右孩子是否为 null ，如果为 null ，需要返回另一个节点 + 1 当作当前节点的深度。

        3.2 代码实现：使用递归实现获取二叉树最小深度

    //使用递归求树的最小深度public int minDepth(TreeNode node) {if (node == null) {return 0;}int l = minDepth(node.left);int r = minDepth(node.right);if (l == 0) {return r + 1;}if (r == 0) {return l + 1;}return Math.min(l,r) + 1;}

        3.3 使用层序遍历实现获取二叉树的最小深度思路

        具体思路为：当带一个遇到的叶子节点时，当前的层数就是该树的最小深度。

        3.4 代码实现：使用层序遍历实现获取二叉树的最小深度

    //使用层序遍历求得树的最小深度public int sequenceMinDepth(TreeNode root) {LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {depth++;int size = queue.size();for (int i = 0; i < size ; i++) {TreeNode poll = queue.poll();if (poll.right == null && poll.left == null) {return depth;}if (poll.left != null) {queue.offer(poll.left);}if (poll.right != null) {queue.offer(poll.right);}}}return depth;}

        

        4.0 翻转二叉树

题目：

        给定一棵二叉树的根节点 root，请左右翻转这棵二叉树，并返回其根节点。

示例 1：

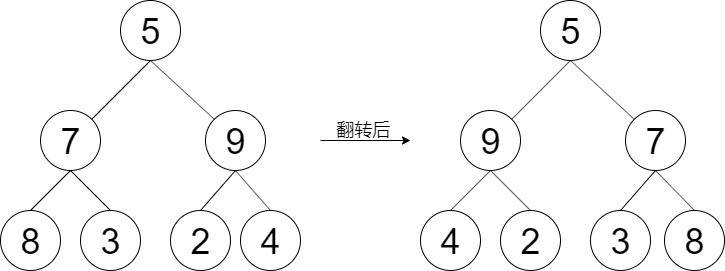
输入：root = [5,7,9,8,3,2,4]
输出：[5,9,7,4,2,3,8]

OJ链接：

LCR 144. 翻转二叉树

        4.1 使用实现递归翻转二叉树思路

        具体思路为：从整体来看，将当前节点的左右节点进行翻转，每一个节点都是如此，递归结束条件为 node == null 时，结束递出。回归到每一个节点的右子树进行翻转。

        4.2 代码实现：使用递归翻转二叉树

    //翻转二叉树public void rollbackRecursion(TreeNode node) {if (node == null) {return;}TreeNode temp = node.left;node.left = node.right;node.right = temp;rollbackRecursion(node.left);rollbackRecursion(node.right);}

        5.0 二叉树经典解法的完整代码

回顾本章代码，进一步巩固：

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;public class TreeNode {private TreeNode left;private int val;private TreeNode right;public TreeNode(int val) {this.val = val;}public TreeNode(TreeNode left, int val, TreeNode right) {this.left = left;this.val = val;this.right = right;}//递归实现前序遍历public void prevRecursion(TreeNode node) {if (node == null) {return;}System.out.print(node.val + " ");prevRecursion(node.left);prevRecursion(node.right);}//递归实现中序遍历public void midRecursion(TreeNode node) {if (node == null) {return;}midRecursion(node.left);System.out.print(node.val + " ");midRecursion(node.right);}//递归实现后序遍历public void postRecursion(TreeNode node) {if (node == null) {return;}postRecursion(node.left);postRecursion(node.right);System.out.print(node.val + " ");}//非递归实现前序遍历public List<Integer> prev(TreeNode root) {TreeNode node = root;LinkedList<TreeNode> stack = new LinkedList<>();List<Integer> list = new ArrayList<>();while (node != null || !stack.isEmpty()) {if (node != null) {stack.push(node);list.add(node.val);node = node.left;}else {TreeNode tp = stack.pop();node = tp.right;}}return list;}//非递归实现中序遍历public void mid(TreeNode root) {TreeNode node = root;LinkedList<TreeNode> stack = new LinkedList<>();while (node != null || !stack.isEmpty()) {if (node != null) {stack.push(node);node = node.left;}else {TreeNode tp = stack.pop();System.out.print(tp.val + " ");node = tp.right;}}System.out.println();}//非递归实现后序遍历public List<Integer> post(TreeNode root) {TreeNode node = root;TreeNode pop = null;List<Integer> list = new ArrayList<>();LinkedList<TreeNode> stack = new LinkedList<>();while ( node != null || !stack.isEmpty()) {if (node != null) {stack.push(node);node = node.left;}else {TreeNode tp = stack.peek();if (tp.right == null || tp.right == pop) {pop = stack.pop();list.add(pop.val);}else {node = tp.right;}}}return list;}//判断对称二叉树public boolean isSymmetry(TreeNode root) {return isSymmetryRecursion(root.left,root.right);}private boolean isSymmetryRecursion(TreeNode left,TreeNode right) {if (left == null && right == null ) {return true;}if (left == null || right == null) {return false;}if (left.val != right.val) {return false;}return isSymmetryRecursion(left.left,right.right) && isSymmetryRecursion(left.right,right.left);}//用递归方式求树的最大深度public int maximumDepthRecursion(TreeNode node) {if (node == null) {return 0;}int l = maximumDepth(node.left);int r = maximumDepth(node.right);return Math.max(l,r) + 1;}//用非递归方式求树的最大深度public int maximumDepth(TreeNode root) {TreeNode curr = root;LinkedList<TreeNode> stack = new LinkedList<>();int max = 0;TreeNode pop = null;while (curr != null || !stack.isEmpty()) {if (curr != null) {stack.push(curr);curr = curr.left;if (max < stack.size()) {max = stack.size();}} else {TreeNode peek = stack.peek();if ( peek.right == null || peek.right == pop ) {pop = stack.pop();}else {curr = peek.right;}}}return max;}//使用层序遍历求树的最大深度public int sequenceMaxDepth(TreeNode root) {if (root == null) {return 0;}LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while ( !queue.isEmpty()) {int size = queue.size();for (int j = 0; j < size; j++) {TreeNode tp = queue.poll();if (tp.left != null) {queue.offer(tp.left);}if (tp.right != null) {queue.offer(tp.right);}//System.out.print(tp.val + " ");}//System.out.println();depth++;}return depth;}//使用递归求树的最小深度public int minDepth(TreeNode node) {if (node == null) {return 0;}int l = minDepth(node.left);int r = minDepth(node.right);if (l == 0) {return r + 1;}if (r == 0) {return l + 1;}return Math.min(l,r) + 1;}//使用层序遍历求得树的最小深度public int sequenceMinDepth(TreeNode root) {LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {depth++;int size = queue.size();for (int i = 0; i < size ; i++) {TreeNode poll = queue.poll();if (poll.right == null && poll.left == null) {return depth;}if (poll.left != null) {queue.offer(poll.left);}if (poll.right != null) {queue.offer(poll.right);}}}return depth;}//翻转二叉树public void rollbackRecursion(TreeNode node) {if (node == null) {return;}TreeNode temp = node.left;node.left = node.right;node.right = temp;rollbackRecursion(node.left);rollbackRecursion(node.right);}}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/211548.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Hello World

Hello World

世界上最著名的程序 from fastapi import FastAPIapp FastAPI()app.get("/") async def root():return {"message": "Hello World"}app.get("/hello/{name}") async def say_hello(name: str):return {"message": f"…
阅读更多...
漏洞扫描服务是什么

漏洞扫描服务是什么

漏洞扫描服务是维护网络安全的重要一环。通过定期或实时的漏洞扫描&#xff0c;组织可以及时发现并修复可能存在的安全威胁&#xff0c;增强自身网络的安全性。在选择漏洞扫描服务时&#xff0c;需要明确自身的需求和目标&#xff0c;并选择合适的工具和服务提供商。只有这样&a…
阅读更多...
flutter使用动态路由传参的最小案例

flutter使用动态路由传参的最小案例

flutter中使用动态路由传递参数的封装案例&#xff0c;子组件页面只需要接收arguments参数即可&#xff0c;参数是一个map&#xff0c;里面包含有所需要的参数&#xff0c;类似于json。在MaterialApp中配置onGenerateRoute&#xff0c;然后动态判断传递参数&#xff1a; route…
阅读更多...
【数据结构】——堆排序

【数据结构】——堆排序

前言&#xff1a;我们已经学习了堆以及实现了堆&#xff0c;那么我们就来给堆进行排序。我们怎么来进行排序呢&#xff1f;这一次我们就来解决这个问题。 如果我们堆排序要求排序&#xff0c;我们是建立大堆还是小堆呢&#xff0c;如果我们建的小堆的话&#xff0c;那我们在排序…
阅读更多...
玩转大数据9：机器学习在大数据分析中的应用

玩转大数据9：机器学习在大数据分析中的应用

1. 引言 在大数据时代&#xff0c;机器学习在大数据分析中扮演着至关重要的角色。本文介绍机器学习在大数据分析中的重要性和应用场景&#xff0c;并探讨Java中可用的机器学习库和框架。 2. 机器学习的基本概念和算法 机器学习是当今人工智能领域的一个关键分支&#xff0c;…
阅读更多...
Flink（九）【时间语义与水位线】

Flink（九）【时间语义与水位线】

前言 2023-12-02-20:05&#xff0c;终于写完啦&#xff0c;最近状态不错。刚写完又收到了她的消息哈哈哈哈&#xff0c;开心。 再去全力打拼一次&#xff0c;奋战一场&#xff0c;就算最后打了败仗也无所谓&#xff0c;至少你留下了足迹。 《解忧杂货店》 1、时间语义 …
阅读更多...
webpack学习-1.起步

webpack学习-1.起步

webpack学习-1.起步 1.基础设置2.配置文件的引入3.总结 1.基础设置 首先 webpack是干嘛的呢&#xff0c;用官网的一张图 Webpack 是一个现代的静态模块打包工具。它主要用于将前端应用程序中的各种资源&#xff08;例如 JavaScript、CSS、图片等&#xff09;打包成一个或多个…
阅读更多...
Linux 进程地址空间

Linux 进程地址空间

文章目录 进程地址空间进程地址空间结构页表虚拟内存写时拷贝 进程地址空间 进程地址空间难以定义&#xff0c;因为它更像是一个中间件。 程序从磁盘中加载到内存&#xff0c;程序的执行需要硬件资源&#xff0c;所以每个程序启动时会创建至少一条进程&#xff0c;进程作为组…
阅读更多...
销售人员如何拓展客户？

销售人员如何拓展客户？

销售这个职业每年都会有很多新人来&#xff0c;也有很多老人转行。大多数人转行的原因无非就是找不到客户&#xff0c;没有完成业绩导致工资不理想&#xff0c;性格不合适无法开口交流不会社交等等。 既然有很多人因为找不到客户而放弃&#xff0c;那么对于一个销售来说&#…
阅读更多...
k8s官方镜像代理加速

k8s官方镜像代理加速

背景 大家可能在云原生领域需要部署周边的一些生态组件时&#xff0c;在国内遇到无法正常拉取镜像&#xff0c;显得就有点苦恼&#xff0c;不过没关系&#xff0c;常见的${{ registry_name }} 例如 “gcr.io”&#xff0c;“registry.k8s.io” Failed to pull image “registry…
阅读更多...
[ffmpeg] aac 音频编码

[ffmpeg] aac 音频编码

aac 介绍 aac 简单说就是音频的一种压缩编码器&#xff0c;相同音质下压缩比 mp3好&#xff0c;目前比较常用。 aac 编码支持的格式 aac 支持的 sample_fmts: 8 aac 支持的 samplerates: 96000 88200 64000 48000 44100 32000 24000 22050 16000 12000 11025 8000 7350 通…
阅读更多...
git push 报错 error: src refspec master does not match any 解决

git push 报错 error: src refspec master does not match any 解决

git报错 ➜ *** git:(main) git push -u origin "master" error: src refspec master does not match any error: failed to push some refs to https://gitee.com/***/***.git最新版的仓库初始化后 git 主分支变成了 main 方法 1.把 git 默认分支名改回 master …
阅读更多...
maven生命周期回顾

maven生命周期回顾

目录 文章目录 **目录**两种最常用打包方法&#xff1a;生命周期&#xff1a; 两种最常用打包方法&#xff1a; 1.先 clean&#xff0c;然后 package2.先 clean&#xff0c;然后install 生命周期&#xff1a; 根据maven生命周期&#xff0c;当你执行mvn install时&#xff0c…
阅读更多...
Python函数

Python函数

1.函数 1.1 函数概述 函数定义和优势 不同形状正方形打印 # 2个 for i in range(0, 2):for j in range(0, 2):print("*", end"")print() # 3个 for i in range(0, 3):for j in range(0, 3):print("*", end"")print() # 4个 for i …
阅读更多...
Linux：dockerfile编写搭建nginx练习（8）

Linux：dockerfile编写搭建nginx练习（8）

dockerfile是创建镜像的一种&#xff0c;通过已有镜像的基础上再在上面部署一些别的。 在这个基础镜像上搭建&#xff0c;我这个是一个空的centos镜像 我这里用http的yum仓库存放了nginx和rpm包 创建dockerfile vim Dockerfile写入#设置基础镜像 FROM centos#维护该镜像的用户…
阅读更多...
redis------在java中操作redis

redis------在java中操作redis

Redis&#xff08;非关系型数据库&#xff09;简介 redis下载 点击即可进入redis中文网进行下载 百度网盘windows版本 提取码 DMH6 redis主要特点 基于内存存储&#xff0c;读写性能高 适合存储热点数据&#xff08;热点商品、资讯、新闻&#xff09; 企业应用广泛 redis不同…
阅读更多...
SQL Server 2016（创建数据库）

SQL Server 2016（创建数据库）

1、实验环境。 某公司有一台已经安装了SQL Server 2016的服务器&#xff0c;现在需要新建数据库。 2、需求描述。 创建一个名为"db_class"的数据库&#xff0c;数据文件和日志文件初始大小设置为10MB&#xff0c;启用自动增长&#xff0c;数据库文件存放路径为C:\db…
阅读更多...
Gti GUI添加标签

Gti GUI添加标签

通过Git Gui打开项目&#xff0c;通过菜单打开分支历史&#xff0c;我这里是名为"develop"的分支 选中需要打标签的commit&#xff0c;右键-Create tag即可 但貌似无法删除标签&#xff0c;只能通过git bash
阅读更多...
linux NAT网卡配置static

linux NAT网卡配置static

由于是内网&#xff0c;资料无法拷贝&#xff0c;借助参考资料&#xff0c;整理发出。 镜像安装 基本操作。 查看VM配置 图1&#xff0c;有几个信息。一个是NAT借用了网卡里的VMnet8适配器。 子网IP是从192.168.142.0 子网掩码255.255.255.255&#xff0c;对应下面配置的N…
阅读更多...
CoreDNS实战(五)-接入prometheus监控

CoreDNS实战(五)-接入prometheus监控

1 背景 Prometheus插件作为coredns的Plugins&#xff0c;默认情况下是内置在coredns中&#xff0c;如果是自己编译安装的版本&#xff0c;需要注意在编译安装的时候的plugin.cfg文件中添加了prometheus:metrics&#xff0c;这样才能确保编译成功。 # 首先我们检查一下运行的版…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023