1. 本文将强化学习方法(MC、Sarsa、Q learning)应用于“S21点的简单纸牌游戏”。
类似于Sutton和Barto的21点游戏示例,但请注意,纸牌游戏的规则是不同且非标准的。
2. 为方便描述,过程使用代码截图,文末附链接。(如果耐心读完的话)
一. S21环境实现
游戏的规则我们设置如下:
- 游戏是用无限副牌进行的(即用替换牌进行采样)
- 从牌组中抽取的每一张牌的值都在1到10之间(均匀分布),颜色为红色(概率0.4)或黑色(概率0.6)。
- 此游戏中没有王牌或图片牌。
- 在游戏开始时,玩家和发牌人都抽到一张黑卡(双方都可以完全观察)
- 每轮玩家可以选择停止拿牌stick或继续拿牌hit
- 如果玩家hit,则从牌组中抽取另一张牌
- 如果玩家stick,她将不会收到更多的牌
- 黑色牌会增加玩家的牌值,红色牌不改牌值(等于无效)
- 如果玩家的总和超过21,或小于1,则她将输掉游戏(奖励-1)
- 如果玩家stick,则发牌人开始它的回合。对于大于等于20的总和,庄家总是保持stick,否则就会继续拿牌hit。如果经销商爆牌,则玩家获胜;否则总和最大的玩家获胜。
- 获胜(奖励+1)、失败(奖励-1)或平局(奖励0)
相比复杂的21点游戏,本游戏主要简化如下:
1. 可以无视前面已发的牌的牌面,不需要根据开始拿到的牌来推断后续发牌的概率。
2. 庄家和玩家分开游戏,并非轮流决定拿牌还是弃牌。
3. 牌值从1-10,且1的值不会变化。
4. 庄家策略固定,总和<20时持续拿牌。
根据任务1,我们针对上述规则定义相关类如下:

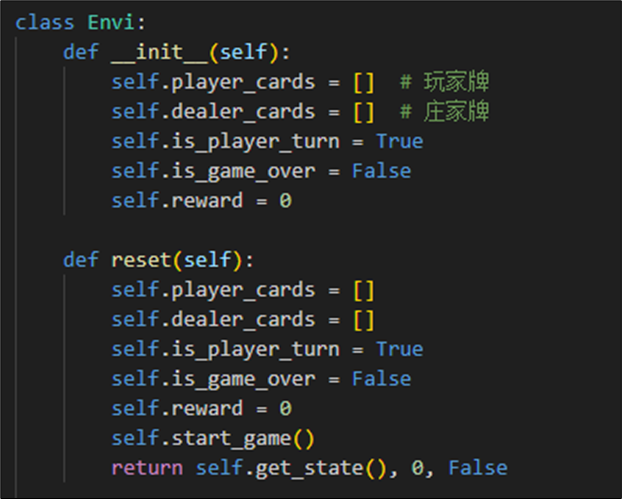
环境类Envi功能如下:
- 主要记录当前玩家和庄家的卡牌,游戏是否结束。
- 在玩家每步step之后 ,返回新的状态、奖励、是否结束标志。
- 当玩家选择stick之后,将后续的所有庄家操作纳入环境中计算。(任务1要求)
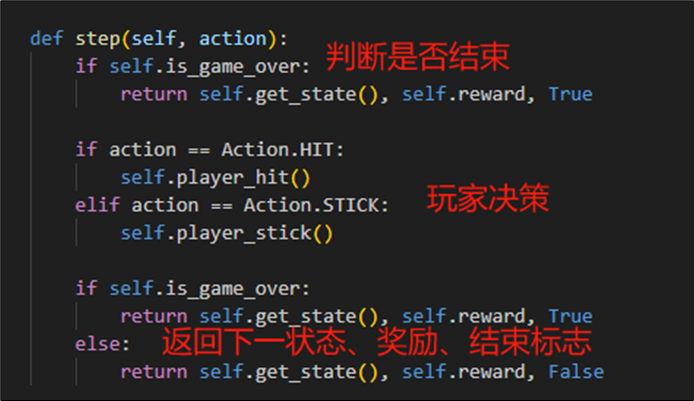
游戏的每步操作step逻辑如下:(其中在玩家决策内更新当前的奖励和状态,存储在环境类对象上)
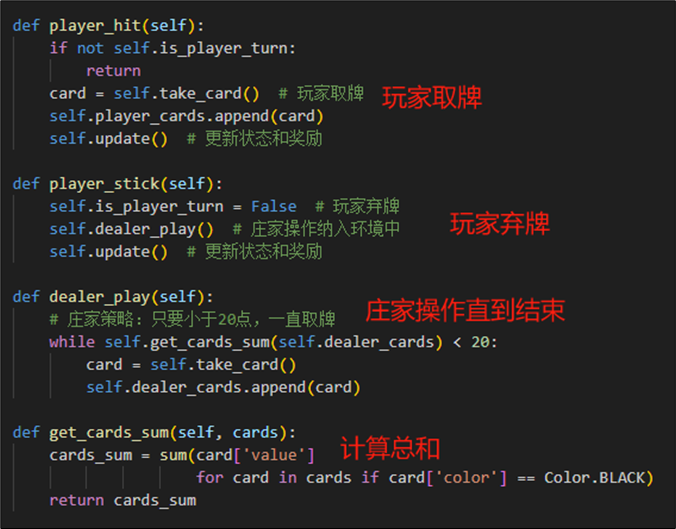
玩家的取牌、弃牌实现如下:
- 当玩家取牌时,增加一张牌到player_cards中,并且更新状态和奖励
- 当玩家弃牌时,转为庄家操作(取牌直到20以上),结束后判定胜负。
实现发牌的操作如下图所示,在1-10之间选择卡牌,并且依照概率赋予颜色。开局必发黑牌。
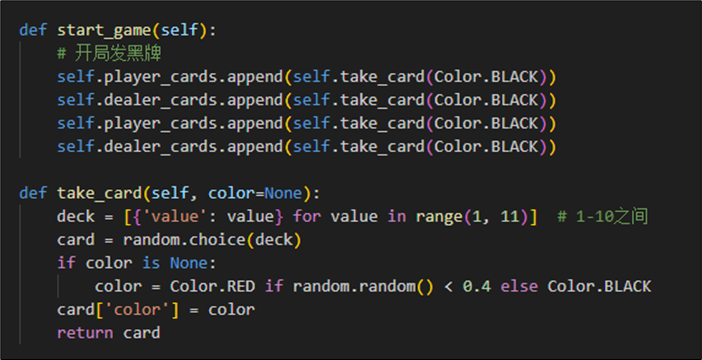
最后,我们根据双方牌值,计算是否发生爆牌的情况或者胜负情况。若玩家仍可继续选择,则继续游戏,更新状态和奖励。

二. 游戏代理实现
2.1 通用代理(玩家类)
我们定义通用代理具有选择动作和训练的基本方法。后续通过不同的策略代理进行继承并实现。(蒙特卡洛代理、Sarsa代理、Q-learning代理)

2.2 蒙特卡洛代理
2.2.1 算法过程
蒙特卡洛方法是一种模型无关(Model Free)的方法,这意味着我们需要通过模拟多次环境交互来估计出策略价值函数。
评估基本步骤如下:
- 生成轨迹: 在每一轮蒙特卡洛模拟中,从环境的初始状态开始,根据当前的策略生成一个完整的轨迹(也称为episode)。轨迹包括状态、动作和即时奖励的序列,直到达到终止状态。
- 计算回报: 对于轨迹中的每个状态,计算从该状态开始的累积回报。回报是从当前状态开始,经过一系列动作和环境反馈后获得的奖励的总和 。在这一环节,我们采用First-Visit MC这种方法,只考虑在一个episode中首次访问某个状态时计算的回报。如果同一个状态在同一个episode中被多次访问,只有第一次访问的回报会被计算在内。这样的话,一个状态在一个episode中只有一个相关的回报值。
- 更新价值函数: 使用得到的回报更新每个状态的价值函数。具体地,对于每个状态,将其之前的价值估计更新为其在多次模拟中获得的平均回报。
- 重复模拟: 重复执行多次模拟,不断累积对状态价值函数的估计。
- 收敛: 当状态价值函数的估计不再发生显著变化时,认为蒙特卡洛策略评估已经收敛。
即基本过程如下:

基于上述分析,我们定义蒙特卡洛代理如下:
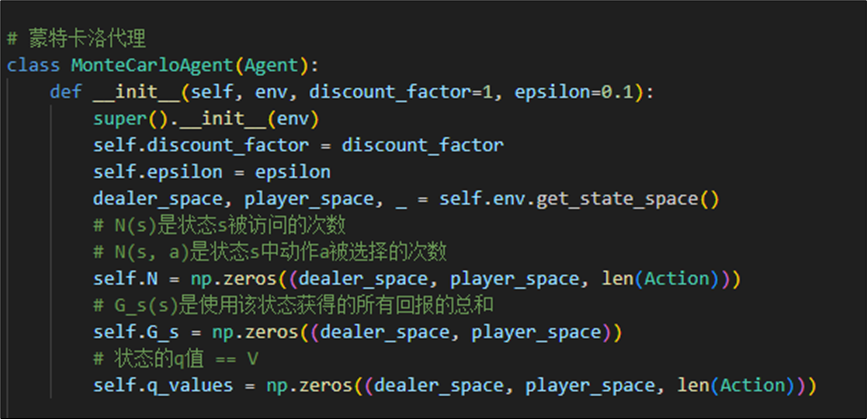
其中属性为折扣因子(默认为1),贪心策略的参数ε,以及计算状态和选择动作的次数N、所有回报总和Gs以及状态价值函数V
2.2.2 动作选择
由于蒙特卡洛需要靠初始策略进行采样,我们设置其采样策略为epsilon 贪心的策略。此策略也可以保证玩家在前期尽可能地去探索,到达所有的牌值状态。
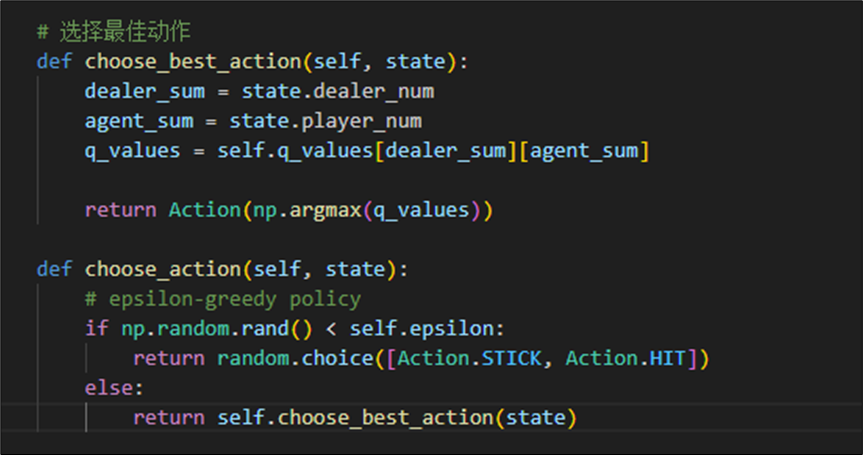
2.2.3 Q值更新
由上图可知,我们采取求累计回报后,再平均更新Q值的方法。实现为:

为了提高性能,我们优化实现为增量式更新期望。
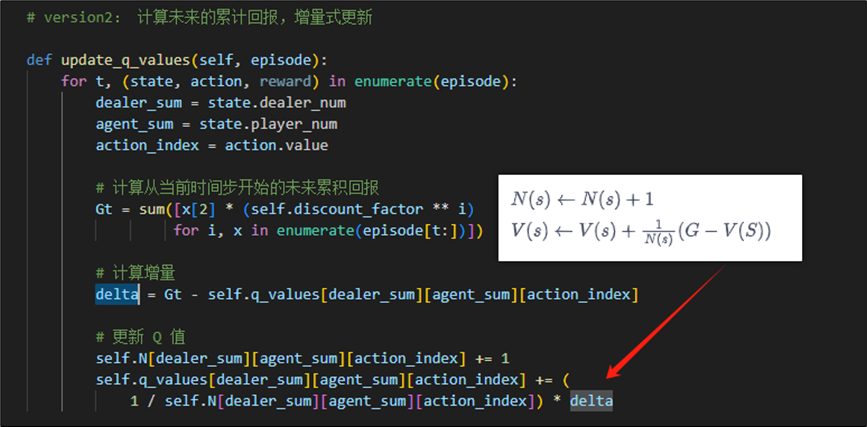
2.2.4 训练agent
训练方法设置如下,在每个迭代里面存储过往的数据到episode,并最后更新状态价值。由于初始的获胜率较低,我们在迭代过程中逐步降低epsilon,以在初期explore,后期exploit。
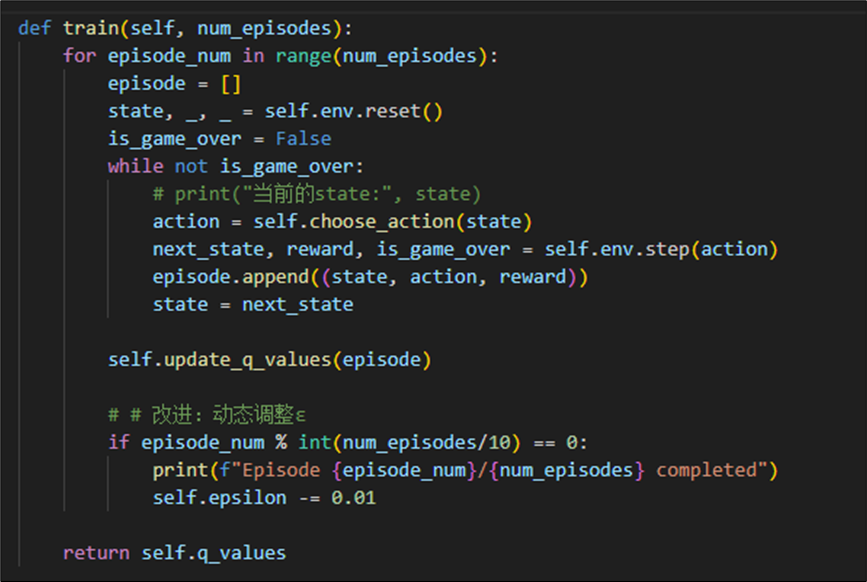
2.2.5 测试agent
我们定义main方法,用于测试并为比较后续不同策略的agent表现。
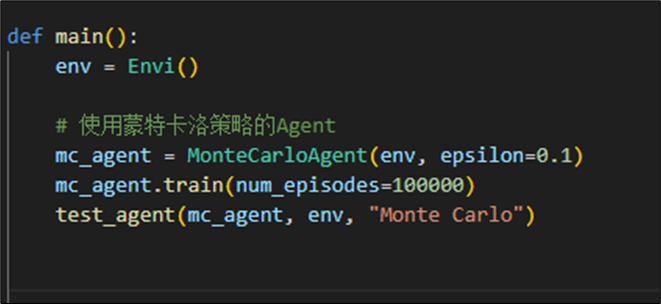
在测试方法test_agent中,我们采取模型认为的最优策略进行游戏,测试10000局并统计游戏结果,计算模型胜率。
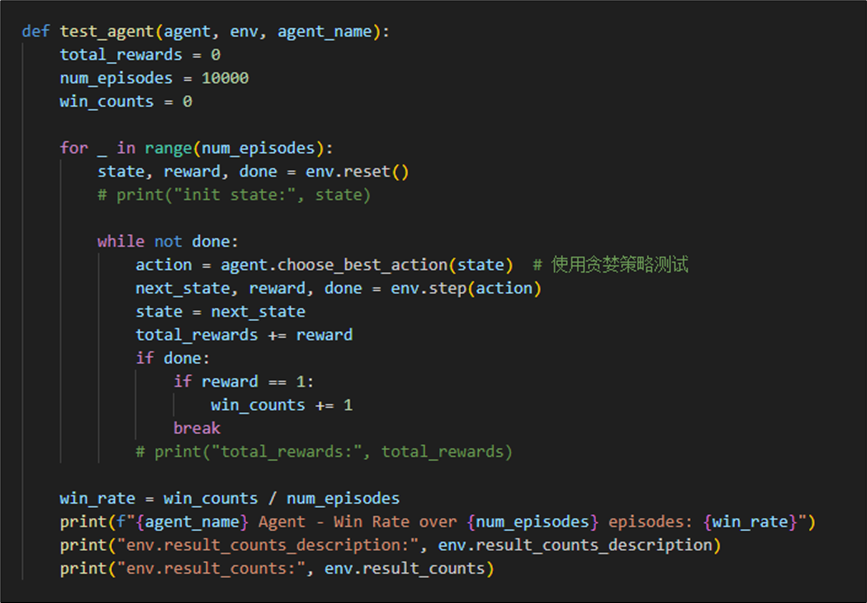
执行结果如下,我们训练10万次后再测试1万次。并且统计每1万次的结局分布。不难发现结局为“庄家爆牌”的概率随着训练次数的增加而不断增加。
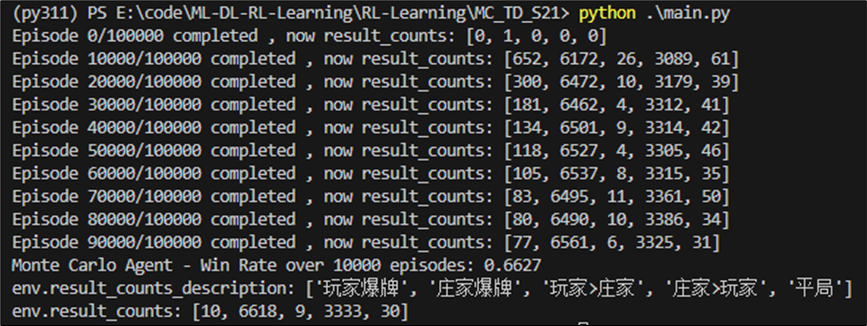
我们可以看到庄家在小于20点持续拿牌的固定策略会导致庄家爆牌的概率极大,但是在不爆牌的情况下,庄家牌值大于玩家牌值的概率较大。综合两者,在多次测试后,可知蒙特卡洛代理的胜率可达66%。
2.2.6 效果分析
为了便于分析,我们编写一个三维可视化的工具函数,主要绘制三幅图:
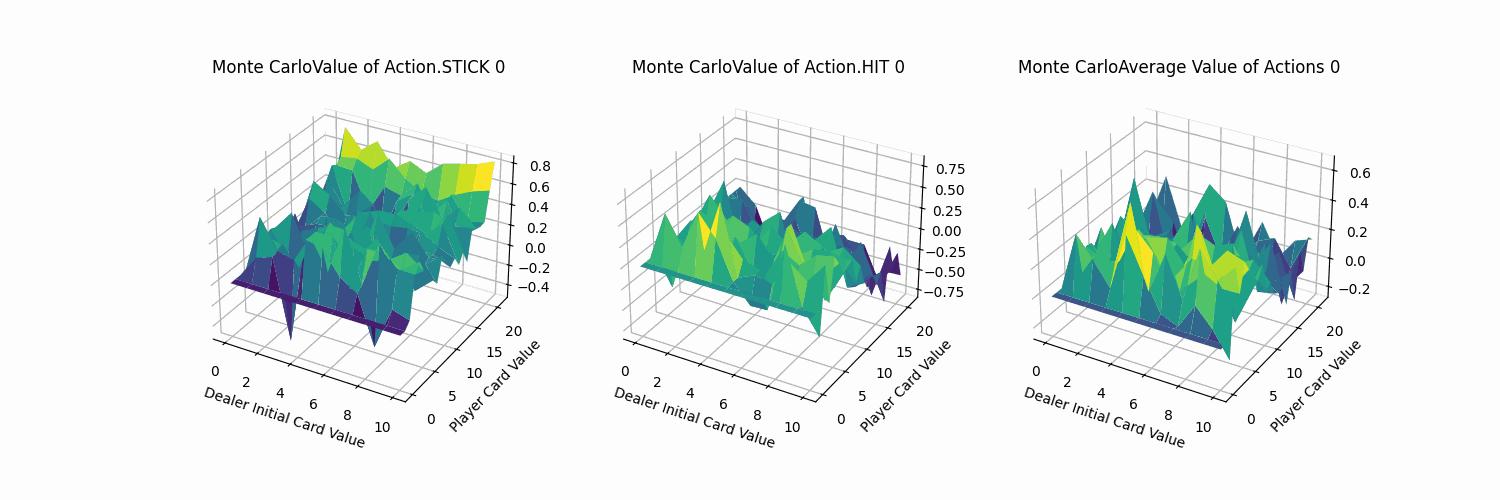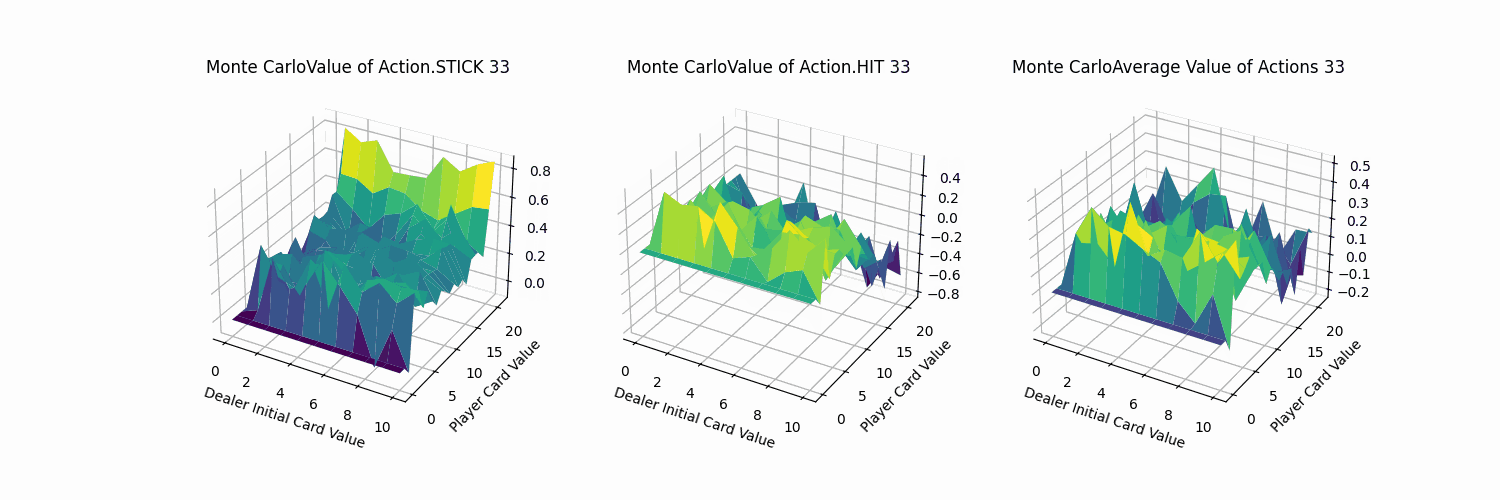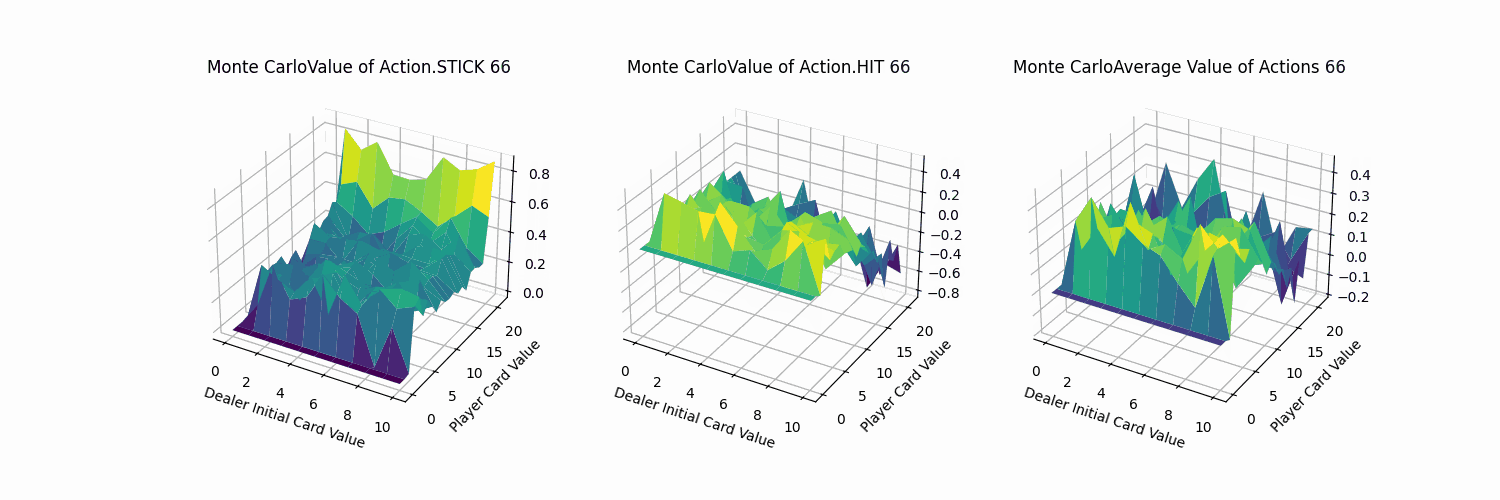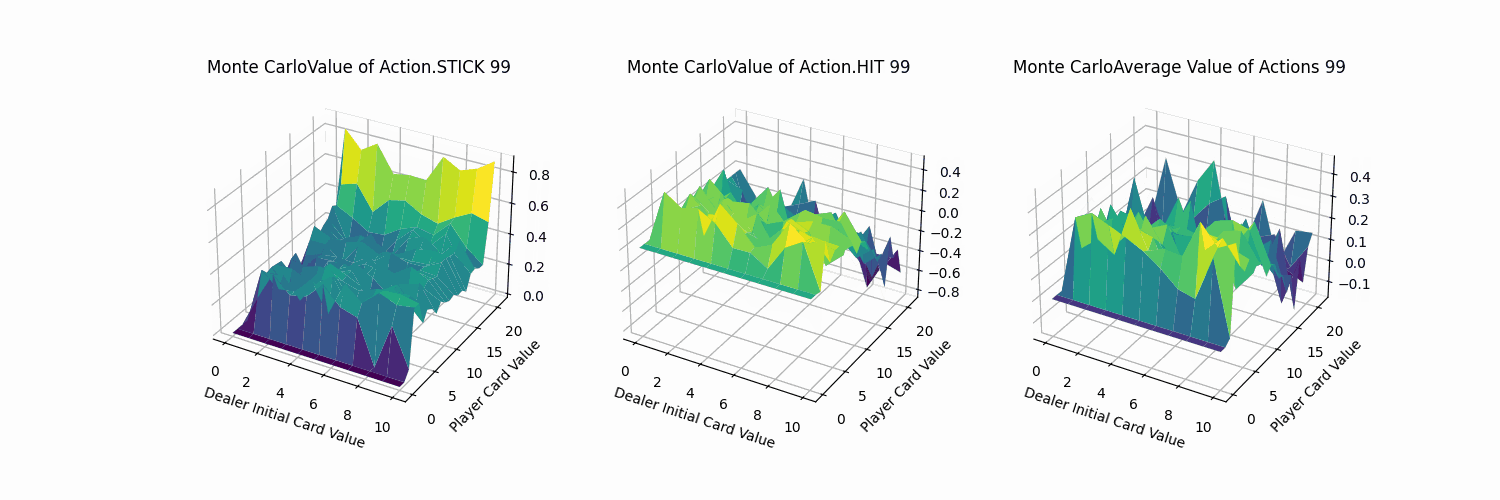
- x、y轴分别表示“庄家初始牌值”,“玩家牌值”,纵轴z轴表示选择第0个动作(Action.STICK)的价值。
- 平面的x、y轴分别表示“庄家初始牌值”,“玩家牌值”,纵轴z轴表示选择第1个动作(Action.HIT)的价值。
- 平面的x、y轴分别表示“庄家初始牌值”,“玩家牌值”,纵轴z轴表示选择两个动作的平均价值。
主要代码如下:
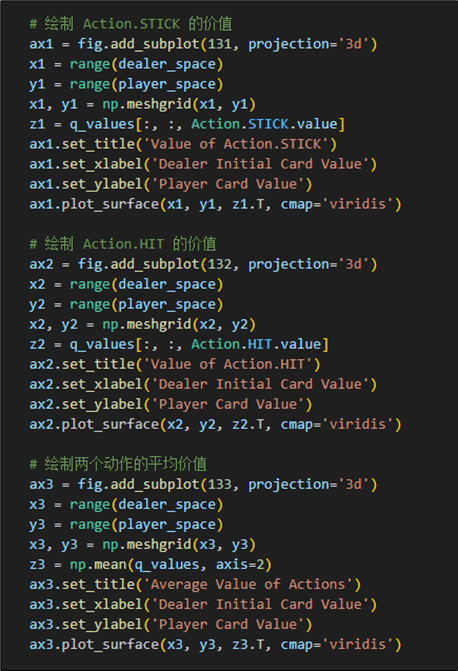
呈现效果如下:
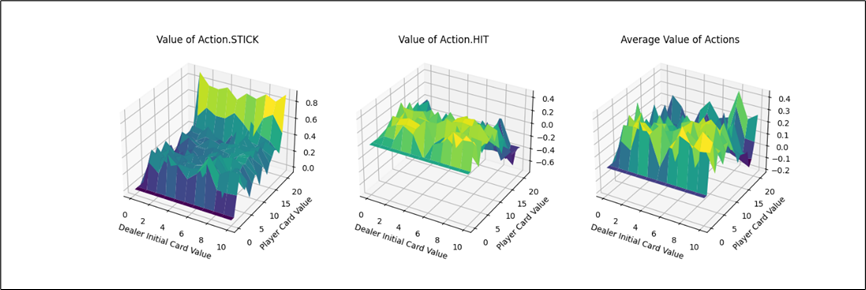
下面我们逐个分析:
- Action.Stick:操作的q值均为正,当牌值逼近21的时候,q值可达到0.8附近,由于+1为胜利的奖励,这也预示着此时胜利概率极大。而由于庄家采取的是低于20牌值持续拿牌的激进策略(容易爆牌)。这意味着选择一个适中的牌值就停止拿牌是一个好的策略。
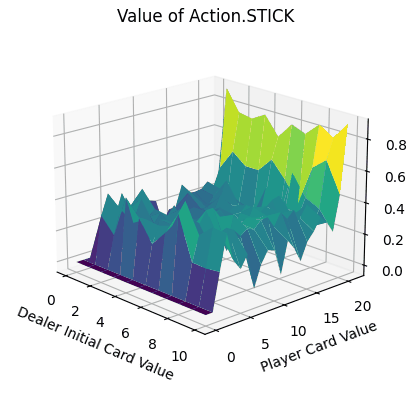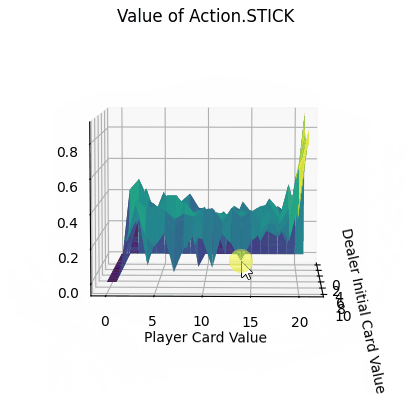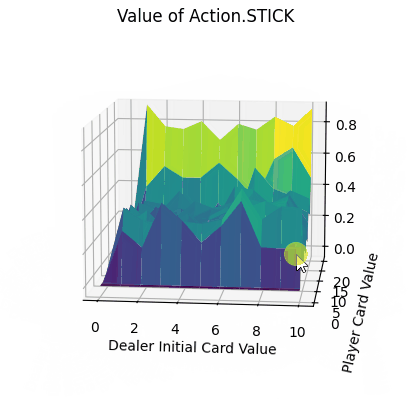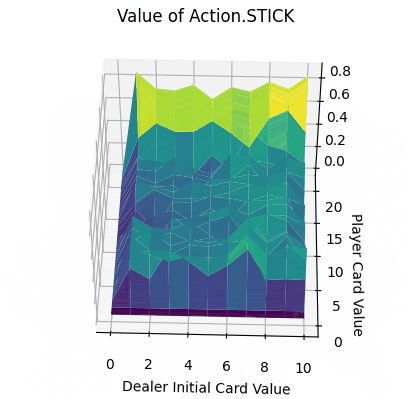
- Action.HIT:操作中Q值存在一些负值,尤其是玩家牌值接近20时,此时拿牌大概率会爆牌,故接近失败的惩罚-1。而在初始牌值小于10的时候,颜色均为浅绿色,此时的agent拿牌会得到一定的奖励。
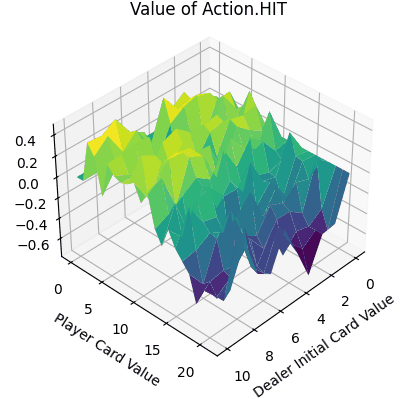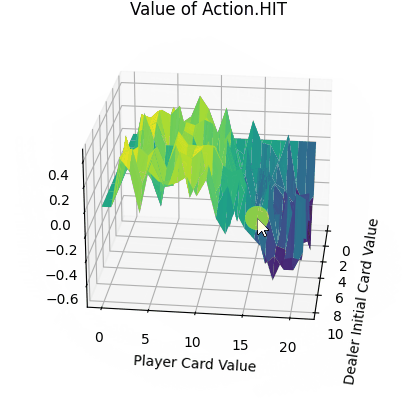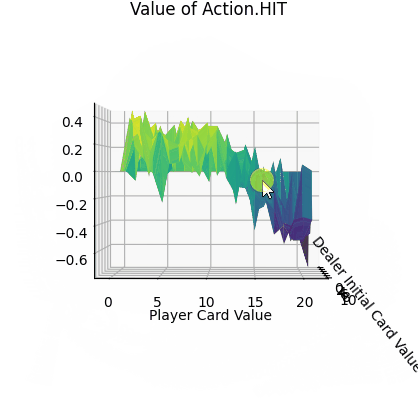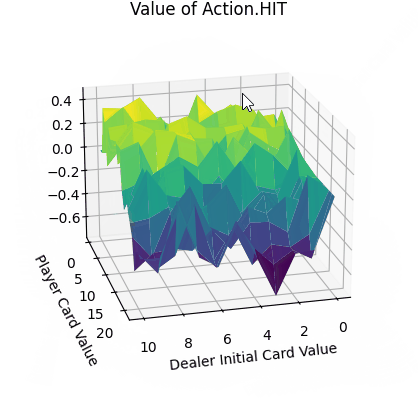
- 平均价值:
- 对比庄家牌轴后,可知在本次实验环境下,仅依靠庄家的初始牌的信息,对玩家决策的意义较小。
- 当玩家牌值约为10时,此时价值较高。牌值从17到20,风险高,Q值较低。
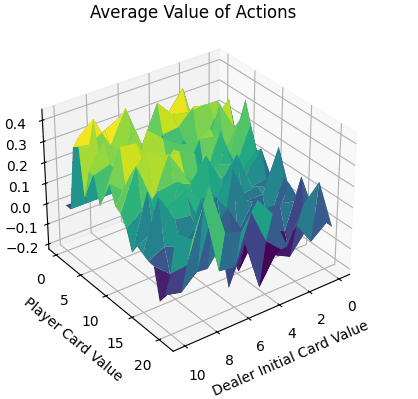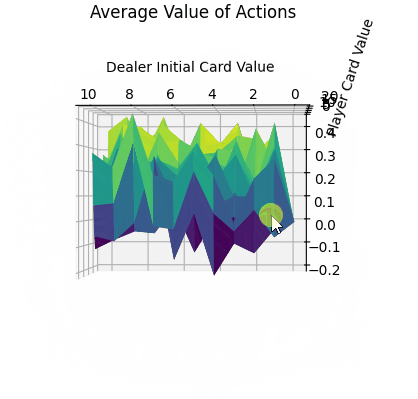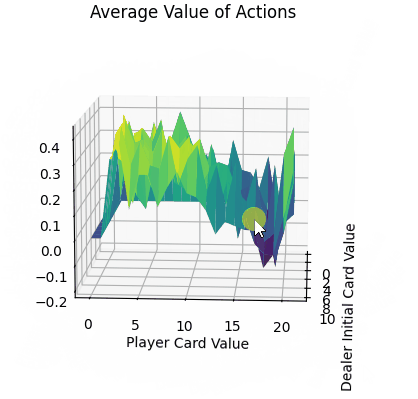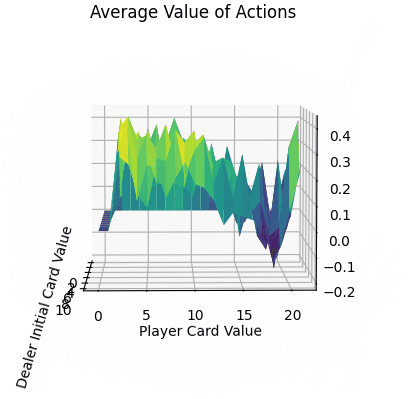
最后通过FuncAnimation库函数实现每隔1000次训练记录,总计100帧的gif。可以看到,随着时间迭代,agent采取单个动作的q_value坡度会渐渐变得平缓。而由于HIT与STICK方法在逼近21点牌值后的决策结果会有较大的不同,所以导致平均价值即便在后期有锯齿状的表面。(相较后续的TD方法,收敛十分平缓。)
2.3 Sarsa代理
2.3.1 算法过程
State-Action-Reward-State-Action这个名称清楚地反应了其学习更新函数依赖的5个值,分别是当前状态S1,当前状态选中的动作A1,获得的奖励Reward,S1状态下执行A1后取得的状态S2及S2状态下将会执行的动作A2。
这是一种在线更新Q值的算法,算法流程大致如下:
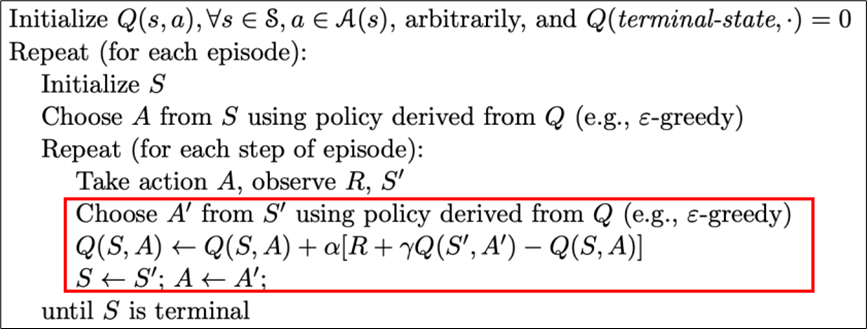
其中在每个episode中,都通过episilon贪心策略选择一个动作,并通过G乘以α(学习率)来更新状态价值Q,重复步骤直到收敛。这里的预期回报G是单步TD(0),即只考虑未来一步收益的。
2.3.2 训练agent
显然,Sarsa代理的最佳决策依旧是选择最优的Q值,而与蒙特卡洛不同只是更新方法。故这里仅展示Sarsas的核心代码,不再赘述相同部分。
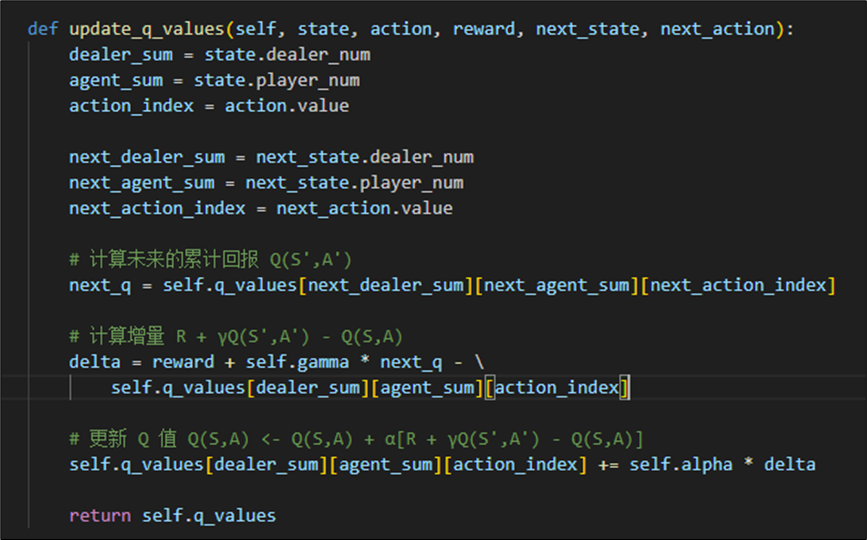
如下所示,为依据上述算法流程实现的训练代码。需要注意的是,当这个状态是最后一个状态时,我们需要判断是否为结束,并且去除公式中下一个状态的Q值。
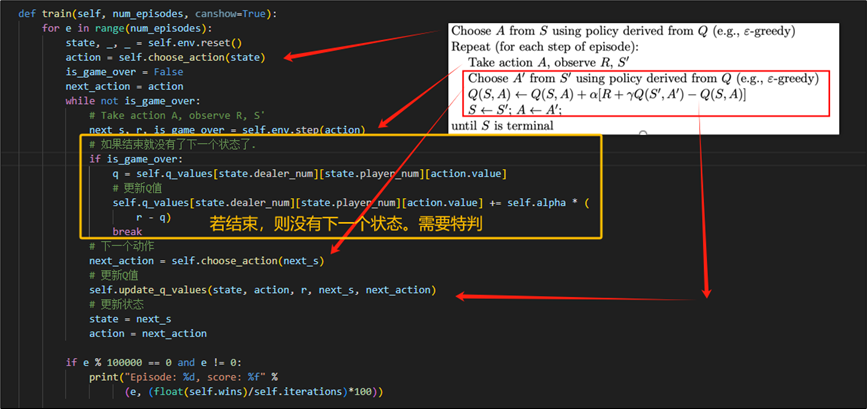
我们依据公式:
实现如下更新Q值函数:
2.3.3 效果分析
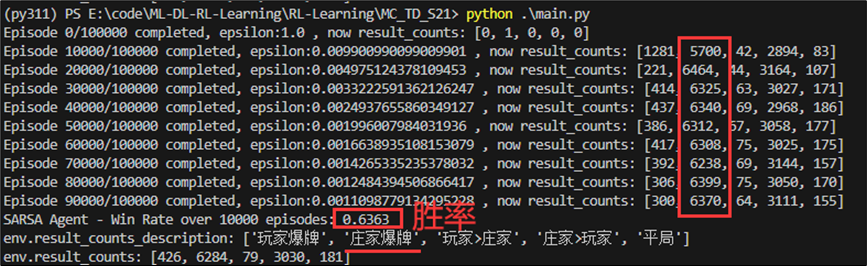
依据上述相同方法,训练10万次并每隔1万次记录对局结果。结果如下:Sarsa的胜率约为0.63,比MC方法(0.66)稍低一点。但是联合MC方法的测试结果可知,胜利原因大部分是因为庄家爆牌而引起。
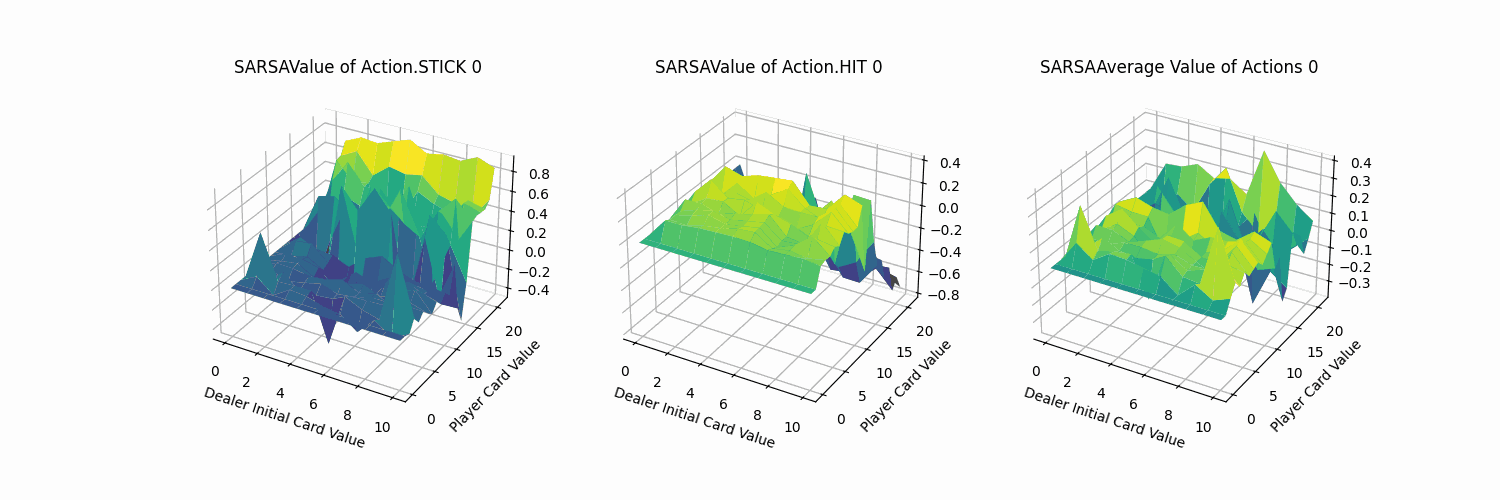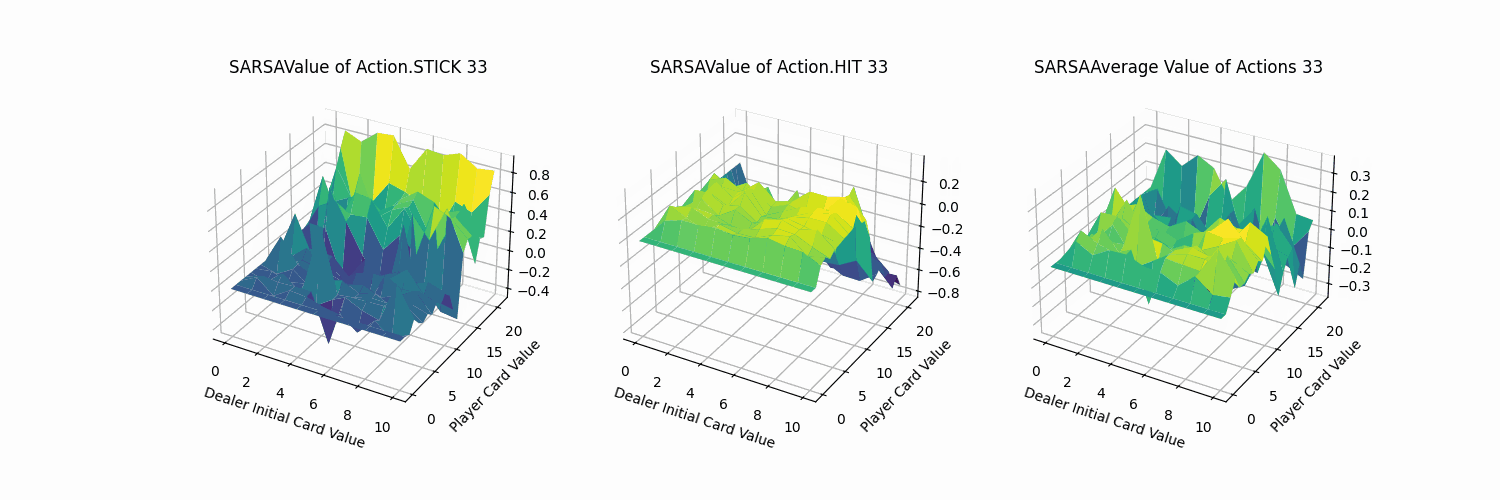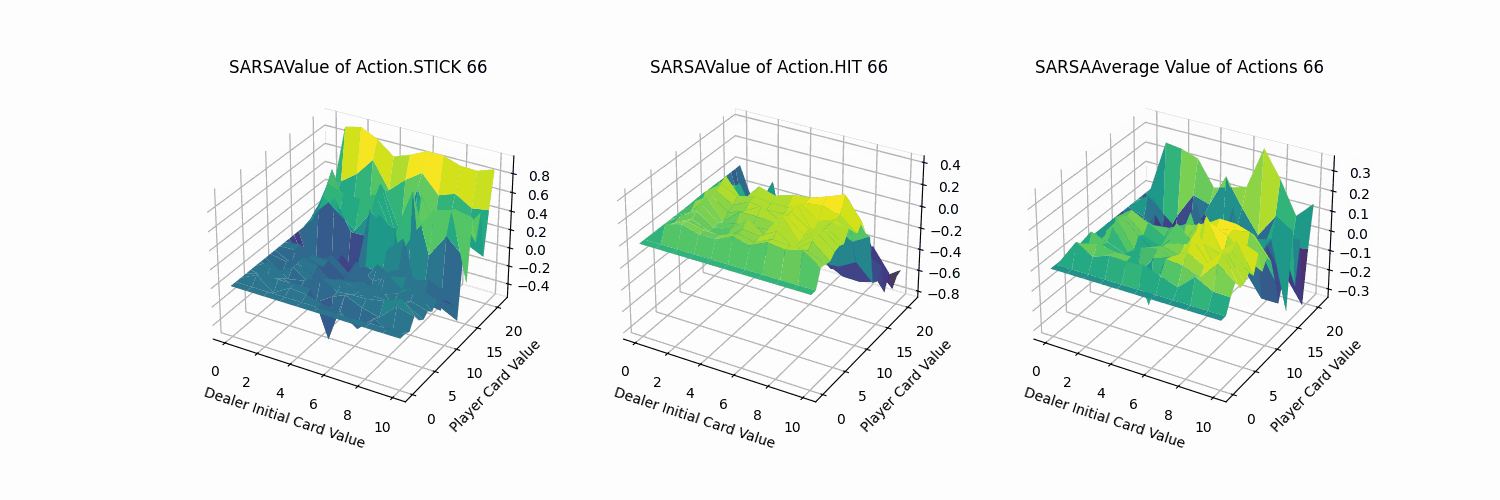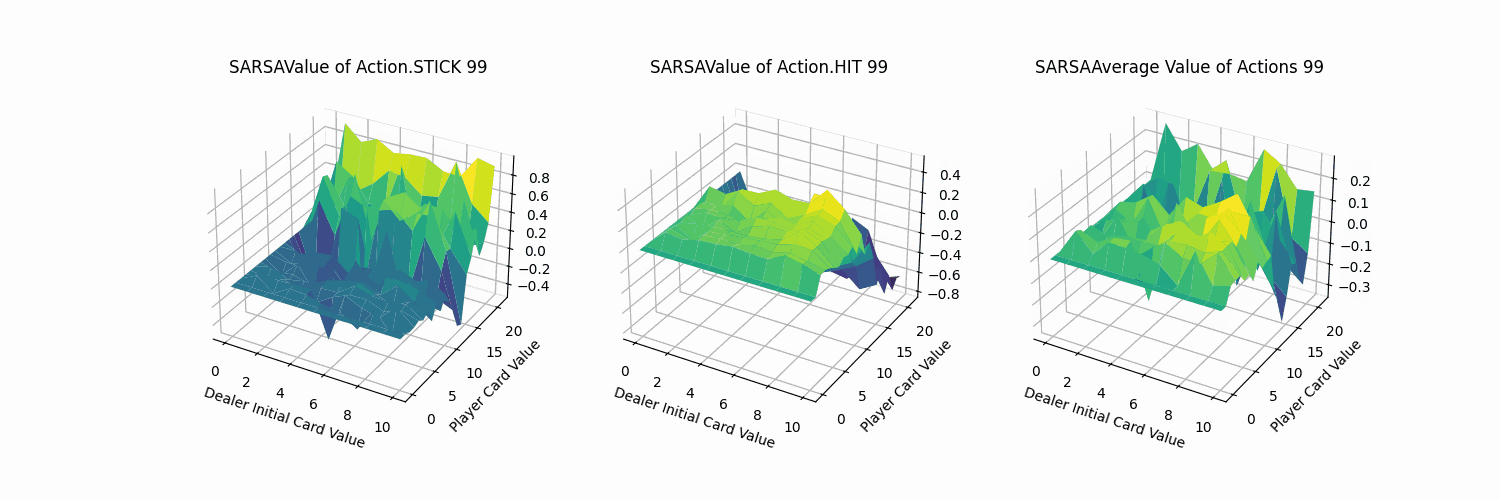
同MC方法进行可视化,可以得到动作STICK、HIT以及平均的状态价值图。
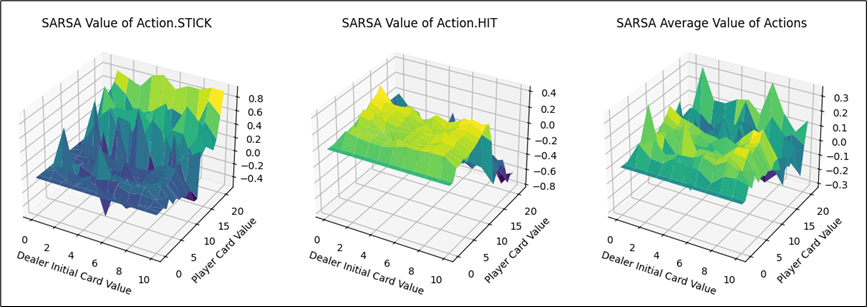
由上图可知,
- 动作STICK和HIT的最优价值分布的牌值区间恰好相反:
- 对于STICK操作而言,牌值越小,STICK奖励越低。牌值接近21时,STICK操作价值越高。
- 对于HIT操作而言,牌值越大,HIT奖励越低。牌值越小,HIT操作价值越高。
- 两者均在牌值约为12的情况下,产生较大的价值差异。分析可知,当牌值取得12时,HIT操作就有可能溢出。
- 从平均结果来看,保持牌值在11以下的平均价值大于高牌值的情况。
- 相比于MC方法的可视化图像,Sarsa方法的价值平面明显更加平滑。
我们取100帧(每帧迭代训练1000次),fps=5的图像叠加为gif查看价值函数的动态收敛过程,除去平均结果外,但看动作STICK与HIT都可清晰地观测到其中变化幅度较大。
2.4 Q-learning代理
2.4.1 算法流程
和Sarsa类似,q-learning也是单步TD方法,但不同的是,它是离线学习的,通过选择当前状态下价值最大的动作来更新Q值。更新公式中使用了max操作。核心公式如下:
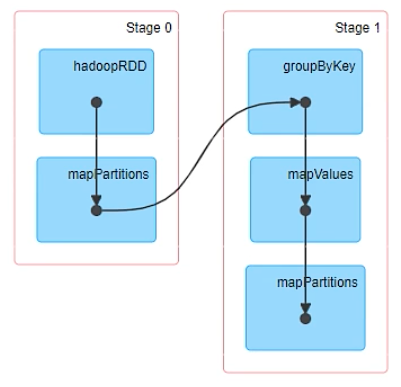
算法流程如下图所示:
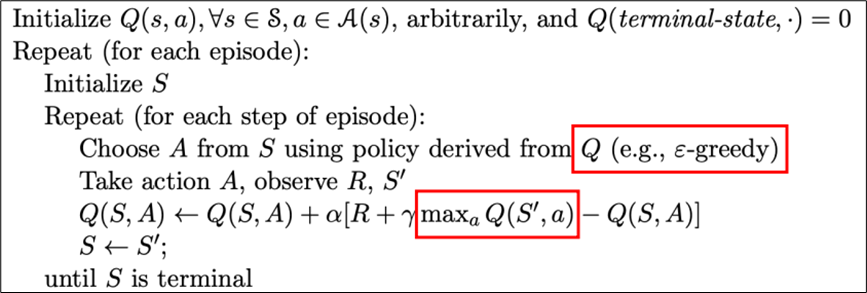
2.4.2 Q值更新
依据上述公式,我们在Sarsa代理的基础上修改值更新部分。核心的“Q值更新”实现如下:
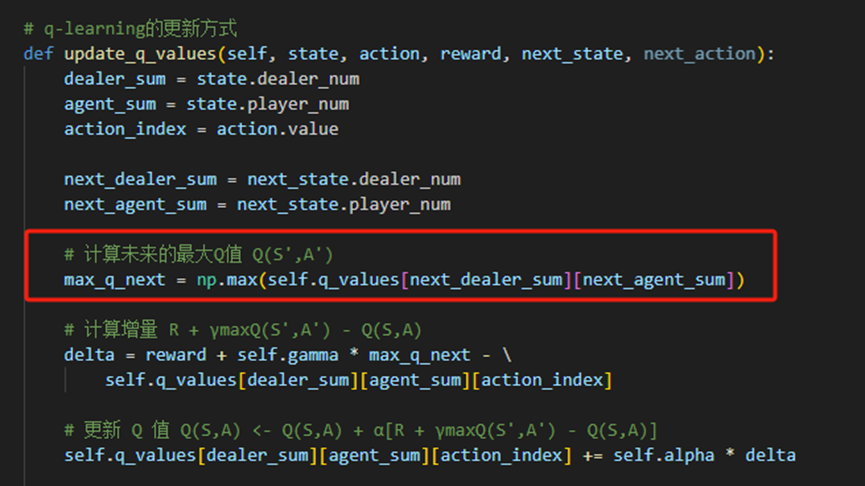
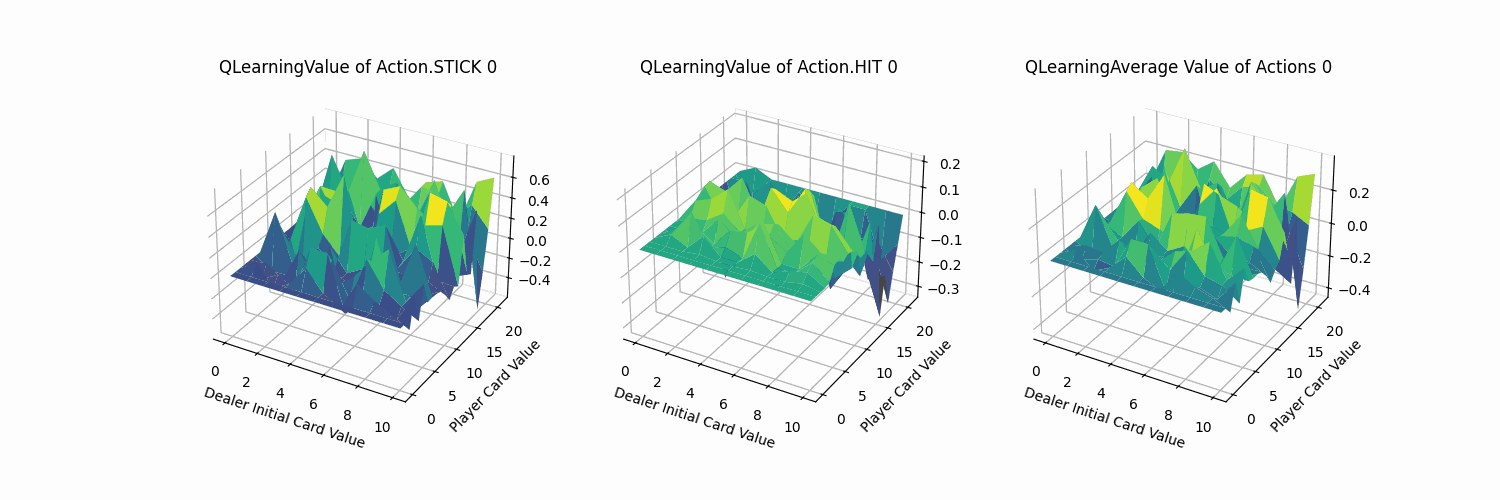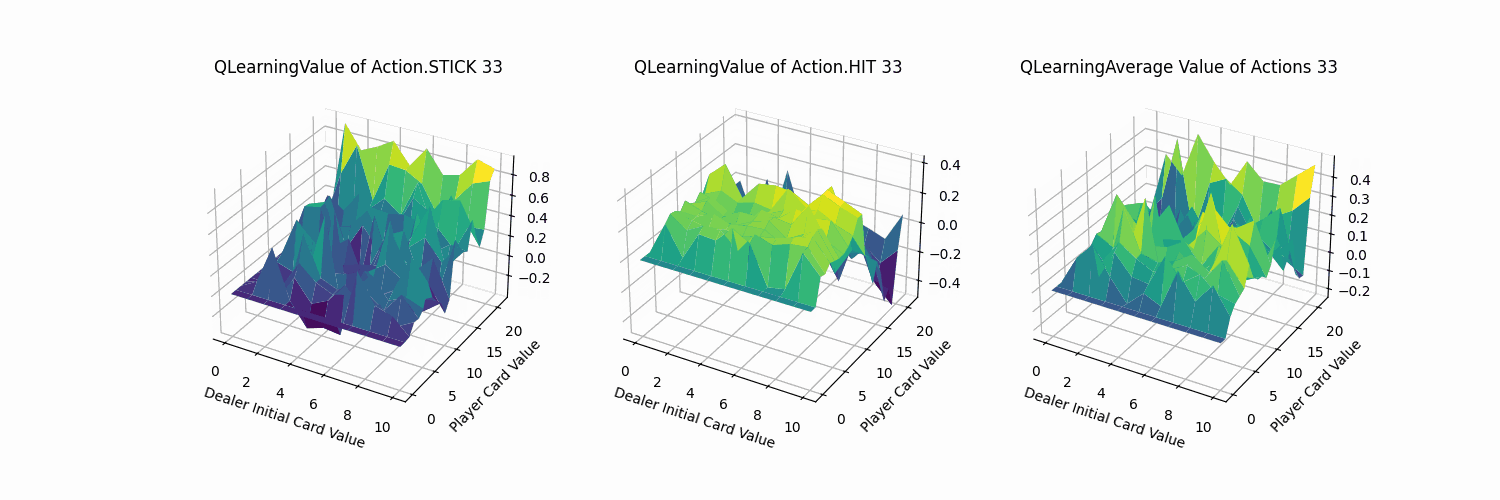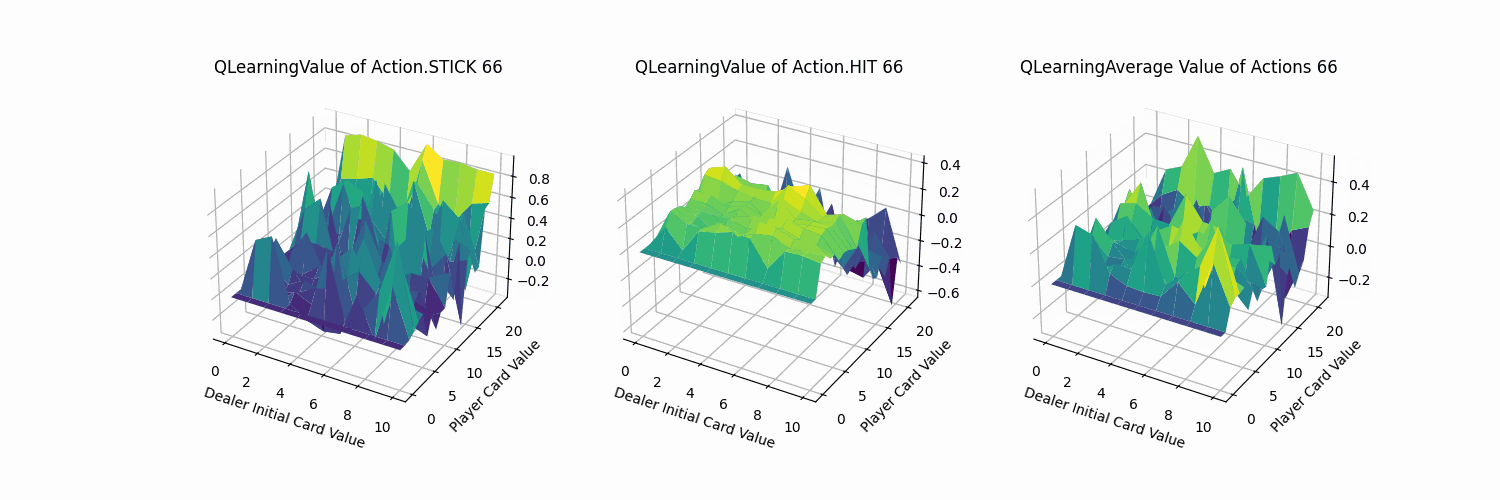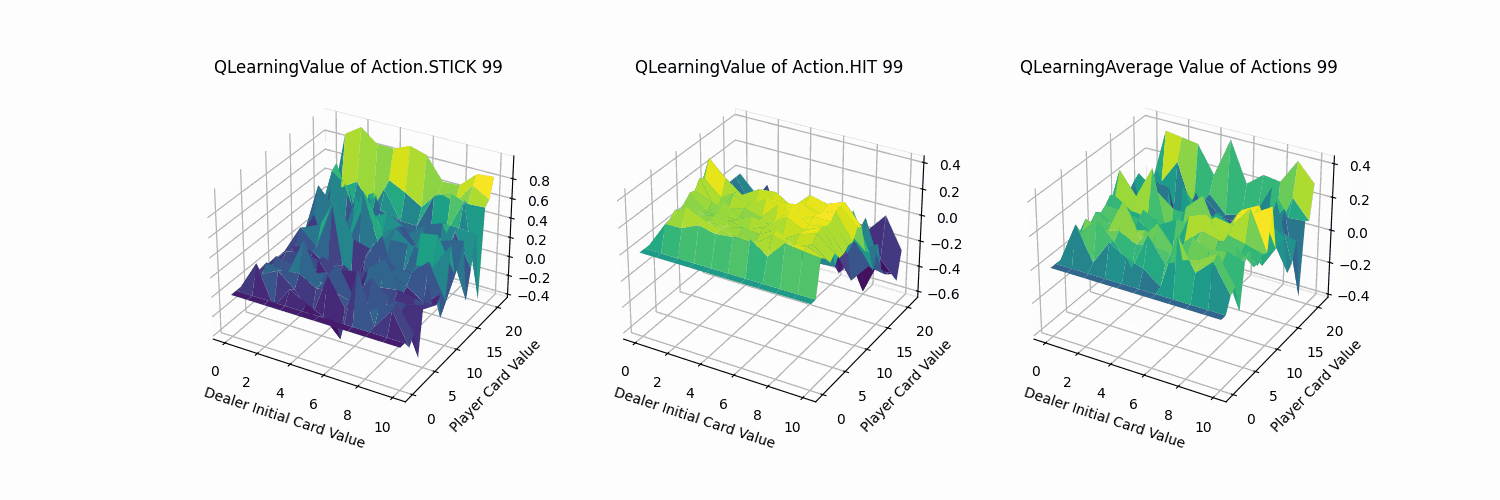
2.4.3 效果分析
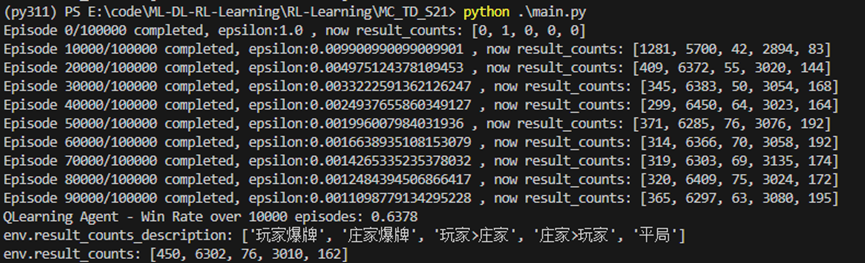
同理,我们测试了Q-learning代理对局结果如下:其胜率为0.6378,与Sarsa代理大致相当。
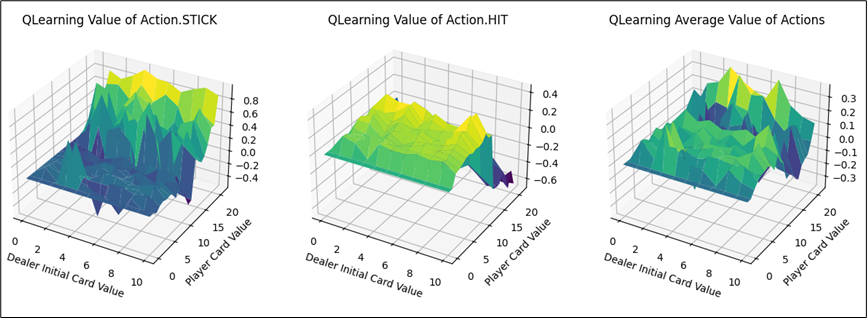
不同动作的价值函数可视化部分如下:大致分布也与Sarsa代理相同。可知在两者收敛的情况下,Q-learning与Sarsa代理实现的策略与效果都是相当的。
观察其收敛过程(1000次训练记录一帧,共100帧),QLearning的迭代过程变化幅度同Sarsa方法,比MC方法更加剧烈。
三. 对比分析
3.1 胜率分析
通过wandb可视化三种代理的胜率情况,我们设置每隔1000次训练进行一次测试,,一共进行100轮。(总计10万次训练)每次测试通过1000次游戏来获取胜率。结果如下:
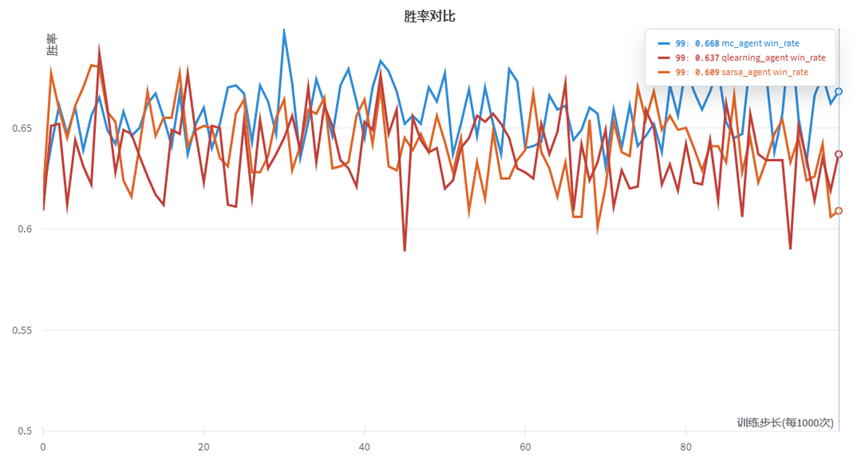
由图可知,胜率较快进入收敛情况,我们采取Smooth可知MC与TD方法的趋势。其中MC方法越到后面(训练10万次后)仍有提升胜率的趋势,而Q-learning与Sarsa方法反而有胜率降低的趋势。(有可能陷入局部最优解。)
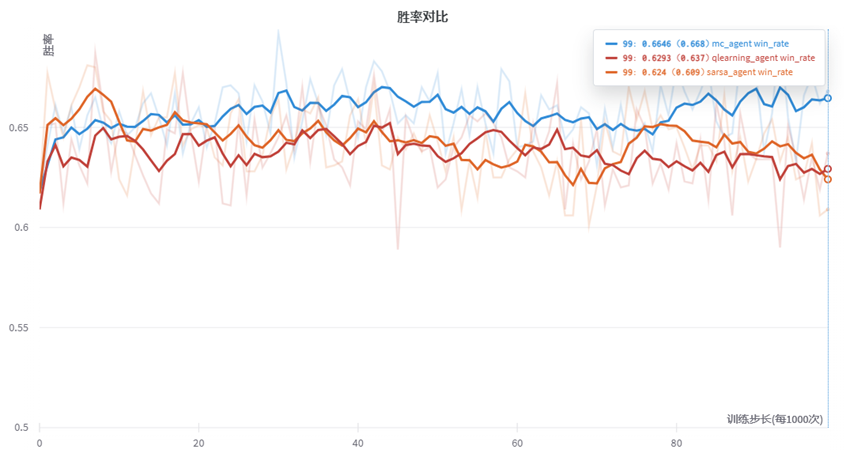
我们缩小训练步长,调整为每隔100次记录1点。得到曲线如下:可以看到,在小规模情况下的三种代理的胜率具有一定的提升,但是幅度较少。
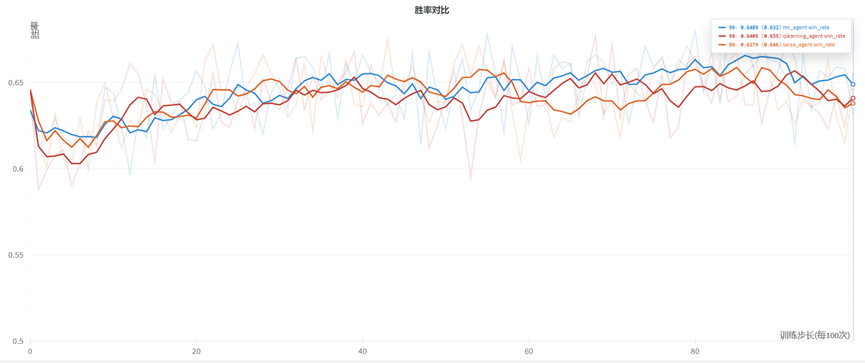
3.2 均方误差对比
我们将三种代理两两比较Q值的均方差,得到三条曲线如下:
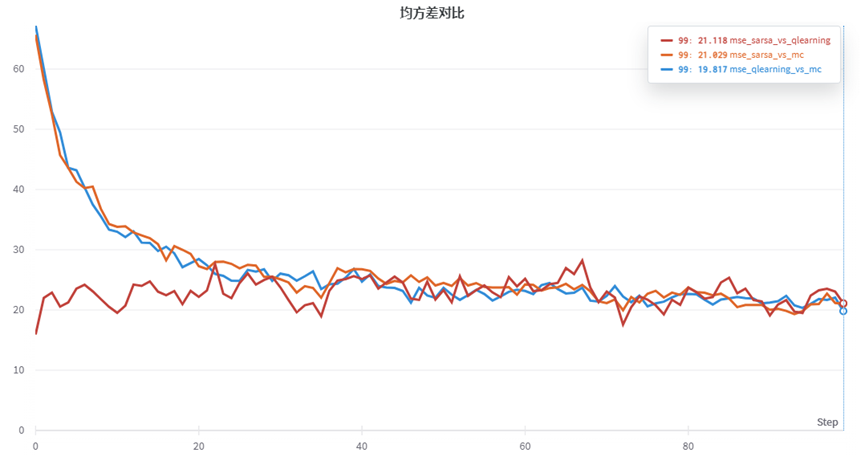
红色为sarsa与qlearning的均方差对比,初始两者相似,随着训练两者均方差有略微提升,后期又会降低。而橙色和蓝色的曲线分别为sarsa、qlearning与mc方法的均方差,初始差异较大,但是后期随着训练增大,也渐渐收敛趋于一致。
3.3 总结
本次实验所应用的三种策略Q-learning、Sarsa和蒙特卡洛都是解决强化学习问题的算法,它们在学习过程中都通过与环境的交互来优化策略。且都用于值函数估计,这三种算法的目标都是学习状态或状态动作对的值函数,即Q值或V值。
区别:
- 更新方式不同:
Q-learning: 使用了离线学习的方式,通过选择当前状态下值最大的动作来更新Q值。更新公式中使用了max操作。
Sarsa: 使用在线学习的方式,通过选择当前状态下的某个动作来更新Q值。更新公式中使用了当前实际选择的动作。
蒙特卡洛: 通过整个回合(episode)的经验来更新值函数,它直接使用了整个回合的累积奖励。
- 探索策略不同:
Q-learning和Sarsa: 使用ε-greedy策略进行探索,以一定概率随机选择动作,以概率1-ε选择当前估计值最高的动作。
蒙特卡洛: 通过在整个回合内的探索来学习。
- 适用场景不同:
Q-learning: 适用于离散状态和动作的问题,能够在未知模型的情况下学习最优策略。
Sarsa: 同样适用于离散状态和动作的问题,但由于使用在线学习,更适合实时决策。
蒙特卡洛: 适用于离散或连续状态和动作的问题,更擅长处理整个回合的经验。
四. 最终代码
https://github.com/YYForReal/ML-DL-RL-Learning/tree/main/RL-Learning/MC_TD_S21







![HLS 2017.4 导出 RTL 报错:ERROR: [IMPL 213-28] Failed to generate IP.](https://img-blog.csdnimg.cn/direct/dd34ed34b085400ca264f79a55f172e7.png)