一、梯度消失与爆炸

在神经网络中，梯度消失和梯度爆炸是训练过程中常见的问题。

梯度消失指的是在反向传播过程中，梯度逐渐变小，导致较远处的层对参数的更新影响较小甚至无法更新。这通常发生在深层网络中，特别是使用某些激活函数（如sigmoid函数）时。当梯度消失发生时，较浅层的权重更新较大，而较深层的权重更新较小，使得深层网络的训练变得困难。

梯度爆炸指的是在反向传播过程中，梯度逐渐变大，导致权重更新过大，网络无法收敛。这通常发生在网络层数较多，权重初始化过大，或者激活函数的导数值较大时。

为了解决梯度消失和梯度爆炸问题，可以采取以下方法：

• 权重初始化：合适的权重初始化可以缓解梯度消失和梯度爆炸问题。常用的方法包括Xavier初始化和He初始化。
• 使用恰当的激活函数：某些激活函数（如ReLU、LeakyReLU）可以缓解梯度消失问题，因为它们在正半轴具有非零导数。
• 批归一化（Batch Normalization）：通过在每个批次的输入上进行归一化，可以加速网络的收敛，并减少梯度消失和梯度爆炸的问题。
• 梯度裁剪（Gradient Clipping）：设置梯度的上限，防止梯度爆炸。
• 减少网络深度：减少网络的层数，可以降低梯度消失和梯度爆炸的风险。

综上所述，梯度消失和梯度爆炸是神经网络中常见的问题，可以通过合适的权重初始化、激活函数选择、批归一化、梯度裁剪和减少网络深度等方法来缓解这些问题。

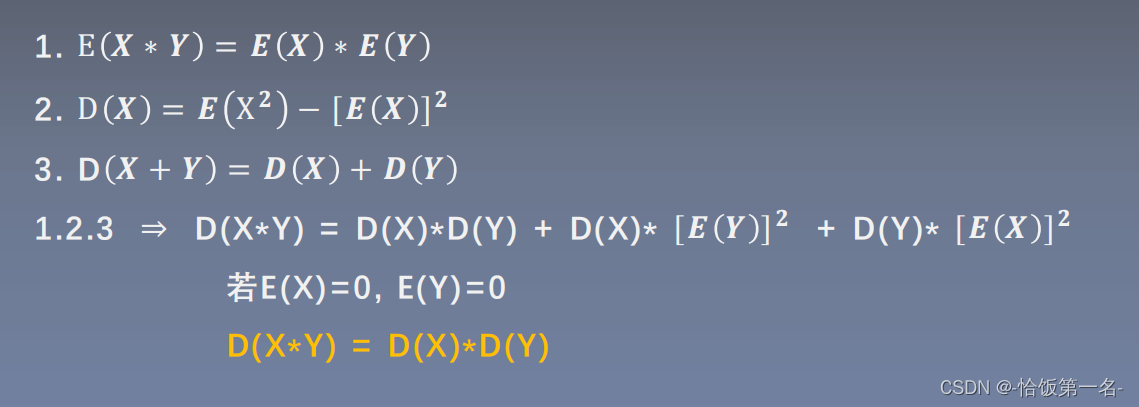
二、Xavier初始化

对于具有饱和函数（如Sigmoid、Tanh）的激活函数和方差一致性的要求，可以推导出权重矩阵的初始化范围。
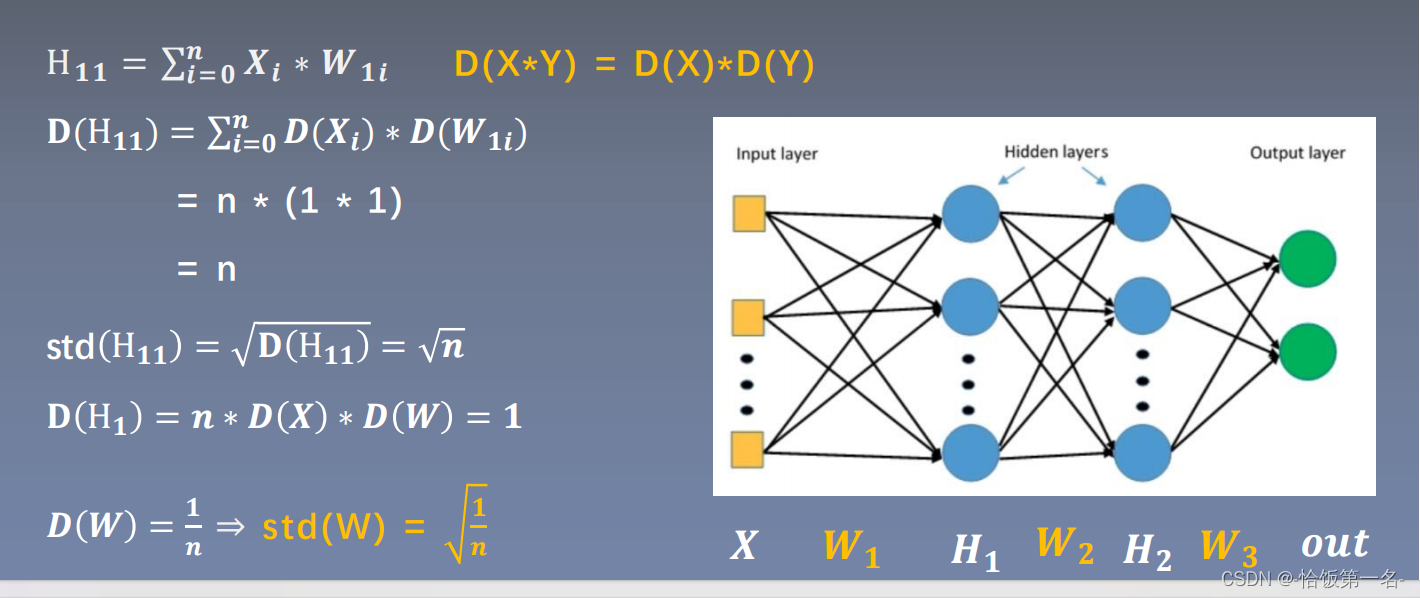
假设输入的维度为 n_in，权重矩阵为 W，我们希望满足方差一致性的要求：

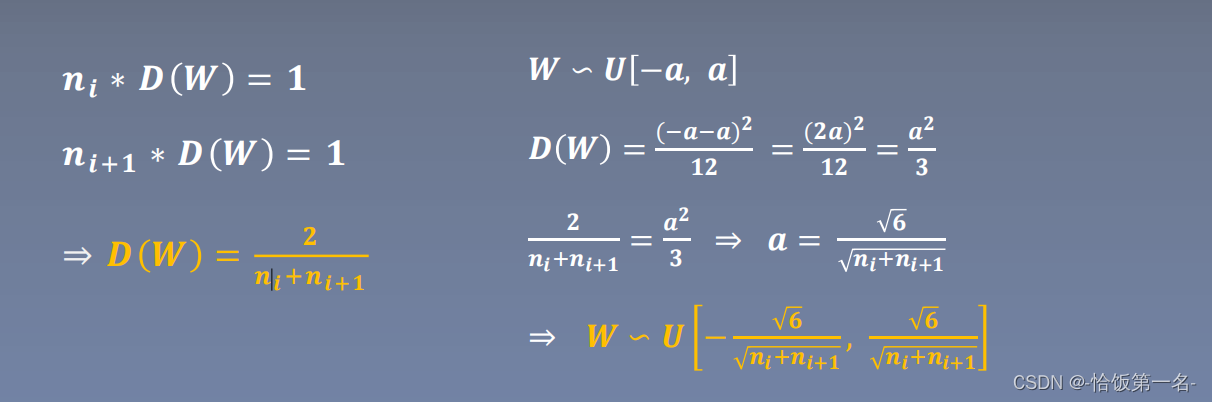
方差一致性：

保持数据尺度维持在恰当范围，通常方差为1

激活函数：ReLU及其变种

---

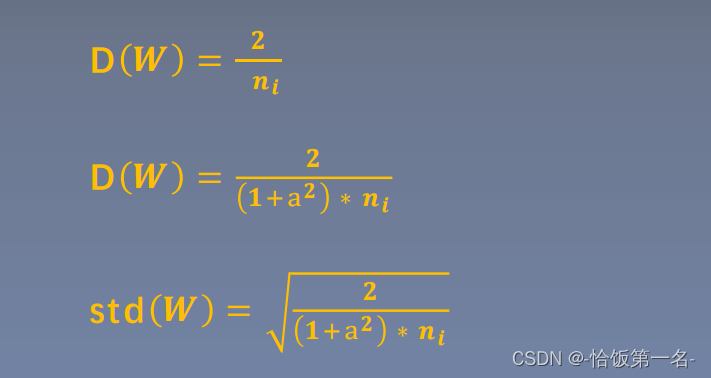
三、十种初始化方法

以下是常用的权重初始化方法：

1. Xavier均匀分布（Xavier Uniform Distribution）：根据输入和输出的维度，从均匀分布中采样权重，范围为 [-a, a]，其中 a = sqrt(6 / (n_in + n_out))。适用于具有饱和函数（如Sigmoid、Tanh）的激活函数。
2. Xavier正态分布（Xavier Normal Distribution）：根据输入和输出的维度，从正态分布中采样权重，均值为 0，标准差为 sqrt(2 / (n_in + n_out))。适用于具有饱和函数的激活函数。
3. Kaiming均匀分布（Kaiming Uniform Distribution）：根据输入维度，从均匀分布中采样权重，范围为 [-a, a]，其中 a = sqrt(6 / n_in)。适用于具有ReLU激活函数的网络。
4. Kaiming正态分布（Kaiming Normal Distribution）：根据输入维度，从正态分布中采样权重，均值为 0，标准差为 sqrt(2 / n_in)。适用于具有ReLU激活函数的网络。
5. 均匀分布（Uniform Distribution）：从均匀分布中采样权重，范围为 [-a, a]，其中 a 是一个常数。
6. 正态分布（Normal Distribution）：从正态分布中采样权重，均值为 0，标准差为 std。
7. 常数分布（Constant Distribution）：将权重初始化为常数。
8. 正交矩阵初始化（Orthogonal Matrix Initialization）：通过QR分解或SVD分解等方法，初始化权重为正交矩阵。
9. 单位矩阵初始化（Identity Matrix Initialization）：将权重初始化为单位矩阵。
10. 稀疏矩阵初始化（Sparse Matrix Initialization）：将权重初始化为稀疏矩阵，其中只有少数非零元素。

不同的初始化方法适用于不同的网络结构和激活函数，选择合适的初始化方法可以帮助网络更好地进行训练和收敛。

nn.init.calculate_gain

nn.init.calculate_gain 是 PyTorch 中用于计算激活函数的方差变化尺度的函数。方差变化尺度是指激活函数输出值方差相对于输入值方差的比例。这个比例对于初始化神经网络的权重非常重要，可以影响网络的训练和性能。

主要参数如下：

• nonlinearity：激活函数的名称，用字符串表示，比如 ‘relu’、‘leaky_relu’、‘tanh’ 等。
• param：激活函数的参数，这是一个可选参数，用于指定激活函数的特定参数，比如 Leaky ReLU 的 negative_slope。

这个函数的返回值是一个标量，表示激活函数的方差变化尺度。在初始化网络权重时，可以使用这个尺度来缩放权重，以确保网络在训练过程中具有良好的数值稳定性。

例如，可以在初始化网络权重时使用 nn.init.xavier_uniform_ 或 nn.init.xavier_normal_，并通过 calculate_gain 函数计算激活函数的方差变化尺度，将其作为相应初始化方法的参数。这样可以根据激活函数的特性来调整权重的初始化范围，有助于更好地训练神经网络。

小案例

import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seedset_seed(1)  # 设置随机种子class MLP(nn.Module):def __init__(self, neural_num, layers):super(MLP, self).__init__()self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])self.neural_num = neural_numdef forward(self, x):for (i, linear) in enumerate(self.linears):x = linear(x)x = torch.relu(x)print("layer:{}, std:{}".format(i, x.std()))if torch.isnan(x.std()):print("output is nan in {} layers".format(i))breakreturn xdef initialize(self):for m in self.modules():if isinstance(m, nn.Linear):# nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))    # normal: mean=0, std=1# a = np.sqrt(6 / (self.neural_num + self.neural_num))## tanh_gain = nn.init.calculate_gain('tanh')# a *= tanh_gain## nn.init.uniform_(m.weight.data, -a, a)# nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)# nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))nn.init.kaiming_normal_(m.weight.data)flag = 0
# flag = 1if flag:layer_nums = 100neural_nums = 256batch_size = 16net = MLP(neural_nums, layer_nums)net.initialize()inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1output = net(inputs)print(output)# ======================================= calculate gain =======================================# flag = 0
flag = 1if flag:# 生成随机张量并通过tanh激活函数计算输出x = torch.randn(10000)out = torch.tanh(x)# 计算激活函数增益gain = x.std() / out.std()print('gain:{}'.format(gain))# 使用PyTorch提供的calculate_gain函数计算tanh激活函数的增益tanh_gain = nn.init.calculate_gain('tanh')print('tanh_gain in PyTorch:', tanh_gain)