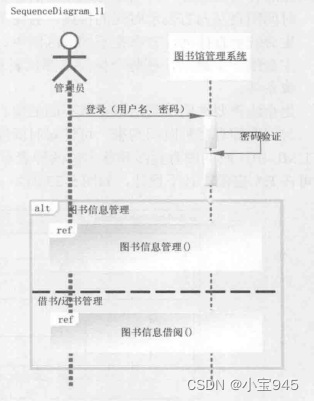
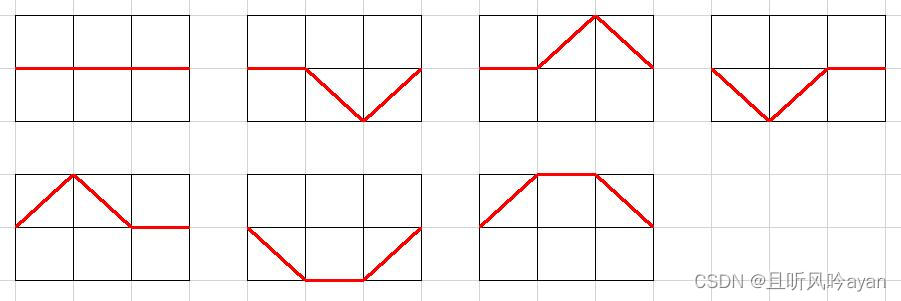
原理
离散余弦变换(DCT)是一种在图像压缩中广泛使用的技术,特别是在JPEG图像格式中。
离散余弦变换(DCT)的作用:DCT的主要目的是将图像从空间域(即像素表示)转换到频率域。在频率域中,图像的信息被表示为不同频率的余弦波的组合。高频成分通常对应于图像中的细节部分(如边缘),而低频成分则对应于图像中的平滑区域。
块大小的影响:
小块大小(如2x2):更小的块能更好地捕捉高频细节,因为它们局限于较小的区域。这导致在变换后的系数中保留了更多的高频信息。然而,这也意味着需要处理更多的块,从而增加了计算量和可能的压缩效率降低。
大块大小(如8x8,JPEG标准中使用):较大的块倾向于捕捉更多的低频信息,且因为它们覆盖了较大的区域,所以可能无法精确表示高频细节(如尖锐边缘)。但是,较大的块通常意味着更高的压缩率,因为在每个块中,许多高频系数可以被忽略(设置为零),而不会显著影响视觉质量。
压缩与质量的权衡:在DCT和图像压缩中,总是存在着数据量(压缩率)和图像质量之间的权衡。压缩图像通常涉及保留更多的低频信息(因为它们对人眼更重要)并丢弃或减少高频信息。块的大小直接影响这种权衡:较小的块提供更好的图像质量但较低的压缩率,而较大的块则提供更高的压缩率但可能牺牲图像的细节质量。
变换系数的阈值处理:在DCT后,通常会对变换系数进行阈值处理,即保留最重要的系数(通常是最大的系数,代表了图像中最显著的频率成分),而将其它系数设置为零。这种方法在大块尺寸下特别有效,因为在这些情况下,仅需要少量的系数就能代表整个块的主要信息。
总结:离散余弦变换(DCT)在图像处理中的应用涉及块大小选择的重要考虑。不同的块大小会影响DCT在压缩效率和图像质量之间的平衡,小块更适合高频细节的保留,而大块更有利于高压缩率的实现,但可能牺牲一些细节质量。理解这些原理有助于在图像压缩和处理中做出更合适的技术选择。
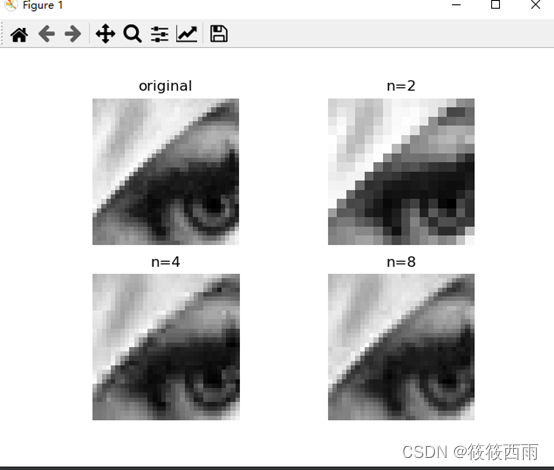
编写代码实现下图

提示
结果图显示了采用不同子图像大小时,仅保留25%的DCT系数重建的图像。只保留25%幅值最大的DCT系数。可以看到,随着子图像尺寸的增大,块效应逐渐减小。
python代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread("lena_eye.tif",0)
img=img.astype(np.float)
rows,cols=img.shape
img_list = [img]
img_name_list = ['original']
blk_size = [2, 4, 8]
for n in blk_size:dct_inv_img = np.zeros(img.shape)coeff_num = int(0.75 * (n**2))for i in range(0, rows, n):for j in range(0, cols, n):dct = cv2.dct(img[i:i+n, j:j+n])dct_amp = np.abs(dct)idx = np.argpartition(dct_amp.ravel(), coeff_num)[:coeff_num]idx2d = np.unravel_index(idx, dct.shape)dct[idx2d] = 0dct_inv_img[i:i+n, j:j+n] = cv2.idct(dct)img_list.append(dct_inv_img)img_name_list.append('n=' + str(n))_, axs = plt.subplots(2, 2)
for i in range(2):for j in range(2):axs[i, j].imshow(img_list[i*2+j], cmap='gray')axs[i, j].set_title(img_name_list[i*2+j])axs[i, j].axis('off')
plt.show()结果展示
DPI
图像尺寸的长度与宽度是以像素为单位的,有的是以厘米为单位。像素与分辨率像素是数码影像最基本的单位,每个像素就是一个小点,而不同颜色的点(像素)聚集起来就变成一幅动人的照片,数码相机经常以像素作为等级分类依据,但不少人认为像素点的多少是CCD光敏单元上的感光点数量,其实这种说法并不完全正确,不少厂商通过特殊技术,可以在相同感光点的CCD光敏单元下产生分辨率更高的数码相片,
图片分辨率越高,所需像素越多,比如:分辨率640×480的图片,大概需要31万像素,2048×1536的图片,则需要高达314万像素。
分辨率可有多个数值,相机提供分辨率越多,拍摄与保存图片的弹性越高。
图片分辨率和输出时的成像大小及放大比例有关,分辨率越高,成像尺寸越大,放大比例越高。
总像素数是指CCD含有的总像素数。不过,由于CCD边缘照不到光线,因此有一部分拍摄时用不上。从总像素数中减去这部分像素就是有效像素
图像分辨率为数码相机可选择的成像大小及尺寸,单位为dpi。常见的有640 x 480;1024 x 768;1600 x 1200;2048 x 1536。在成像的两组数字中,前者为图片宽度,后者为图片的高度,两者相乘得出的是图片的像素。长宽比一般为4:3。
在大部分数码相机内,可以选择不同的分辨率拍摄图片。一台数码相机的像素越高,其图片的分辨率越大。分辨率和图象的像素有直接的关系,一张分辨率为640 x 480的图片,那它的分辨率就达到了307200,也就是我们常说的30万像素,而一张分辨率为1600 x 1200的图片,它的像素就是200万。这样,我们就知道,分辨率表示的是图片在长和宽上占的点数的单位。台数码相机的最高分辨率就是其能够拍摄最大图片的面积。在技术上说,数码相机能产生在每寸图像内,点数最多的图片,通常以dpi为单位,英文为Dot per inch。分辨率越大,图片的面积越大。像素越大,分辨率越高,照片越清晰,可输出照片尺寸也可以越大。