【促销定价】背后的算法技术3-数据挖掘分析

【促销定价】背后的算法技术3-数据挖掘分析

    • 01 整体分析
      • 1）整体概览
      • 2）类别型特征概览
      • 3）数值型特征概览
    • 02 聚合分析
      • 1）天维度
      • 2）品维度
      • 3）价格维度
      • 4）数量维度
    • 03 相关分析
      • 1）1级品类
      • 2）2级品类
      • 3）3级品类
      • 4）sku
    • 04 聚类分析
    • 05 核心结论
    • 06 小结
      • 参考文献

导读：在日常生活中，我们经常会遇见线上/线下商家推出各类打折、满减、赠品、新人价、优惠券、捆绑销售等促销活动。一次成功的促销对于消费者和商家来说是双赢的。一方面，促销活动能让消费者买到低价的商品；另一方面，促销活动也能为商家带来可观的利润。因此，对于商家来说，如何科学合理地制定促销策略是必须仔细思考的问题。

作者1：张哲铭，算法专家，某互联网大厂
作者2：向杜兵，算法专家，某制造业龙头

大家好！我们是IndustryOR团队，致力于分享业界落地的OR+AI技术。欢迎关注微信公众号/知乎【运筹匠心】 。本期我们来谈一谈《促销定价背后的算法技术》。促销活动五花八门、玩法多变，但其底层的核心商业逻辑是“价格”。因此，本期案例将选择某零售商超“促销定价”场景，共分5篇文章依次讲解：（1）业务问题拆解；（2）数据预处理生成；（3）数据挖掘分析；（4）模型算法实现-价格弹性模型；（5）模型算法实现-运筹决策模型。

本篇文章讲解（3）数据挖掘分析。

共分为4个部分，依次为：
01 整体分析
02 聚合分析
03 相关分析
04 聚类分析
05 核心结论

注：本案例数据改编自【2019年全国大学生数学建模E题】公开数据集。

01 整体分析

经过（2）数据预处理生成，我们将订单中的SKU销量聚合至日维度，生成了待分析求解的促销定价数据大宽表（promotional_pricing_data1.csv），表结构如下：

  • 促销定价数据大宽表
字段含义
sku_id商品ID
sku_name商品名称
ori_prc原价
sale_prc售价
cost_prc成本价
sku_cnt销量
cate1_id一级类目id
cate2_id二级类目id
cate3_id三级类目id
cate1_name一级类目名称
cate2_name二级类目名称
cate3_name三级类目名称
sale_dt销售日期

1）整体概览

图片图片

我们发现，经过（2）数据预处理生成加工后的数据集共有1105365条样本，无空值。

2）类别型特征概览

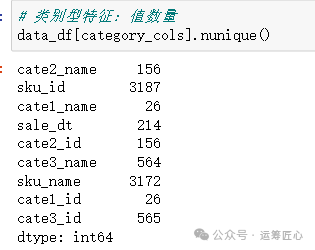图片类别型特征

3）数值型特征概览

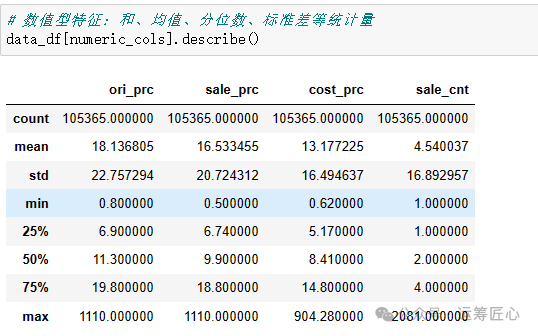图片我们发现，数据共有3187种sku，1级品类26种、2级品类156种、3级品类565种。75%的商品售价不高于18.8、日销量不超过4个，但也有超过千元的高价品和销量过千的高销品。

02 聚合分析

为了进一步挖掘数据，我们分别在天维度、品维度、价格维度和数量维度对数据进行聚合分析。

1）天维度

统计每日的销量、GMV(销售额)、成本、毛利额、折扣率等信息，画出趋势图。

# 各日期下的销量、GMV(销售额)、成本、毛利额、折扣率等  
data_df['gmv'] = data_df['sale_prc'] * data_df['sale_cnt']  
data_df['cost'] = data_df['cost_prc'] * data_df['sale_cnt']  
data_df['profit'] = data_df['gmv'] - data_df['cost']  
data_df['discount'] = 1 - data_df['sale_prc'] / data_df['ori_prc']  
data_df['discount_amount'] = data_df['ori_prc'] - data_df['sale_prc']  
ret_df = IOR_DP.group_agg(df=data_df,   grp_cols=['sale_dt'],   agg_dict={'sale_cnt': 'sum', 'gmv': 'sum', 'cost': 'sum',  'profit': 'sum', 'discount': 'mean'})  
ret_df['profit_ratio'] = ret_df['profit_sum'] /  ret_df['cost_sum']  
ret_df = ret_df.sort_values(by='sale_dt')  pic1 = ret_df.plot(x='sale_dt', y=['gmv_sum', 'cost_sum', 'profit_sum', 'sale_cnt_sum'],  secondary_y= 'sale_cnt_sum', title = '日gmv/成本/毛利额/销量趋势图',  kind='line', figsize=(20, 5), fontsize=18)  pic2 = ret_df.plot(x='sale_dt', y=['profit_ratio', 'profit_sum', 'sale_cnt_sum'],   secondary_y= 'profit_ratio', title = '日毛利率/毛利额/销量趋势图',  kind='line', figsize=(20, 5), fontsize=18)  pic3 = ret_df.plot(x='sale_dt', y=['discount_mean', 'sale_cnt_sum'], secondary_y= 'discount_mean',  title = '日平均折扣/销量趋势图', kind='line', figsize=(20, 5), fontsize=18)  plt.show([pic1, pic2, pic3])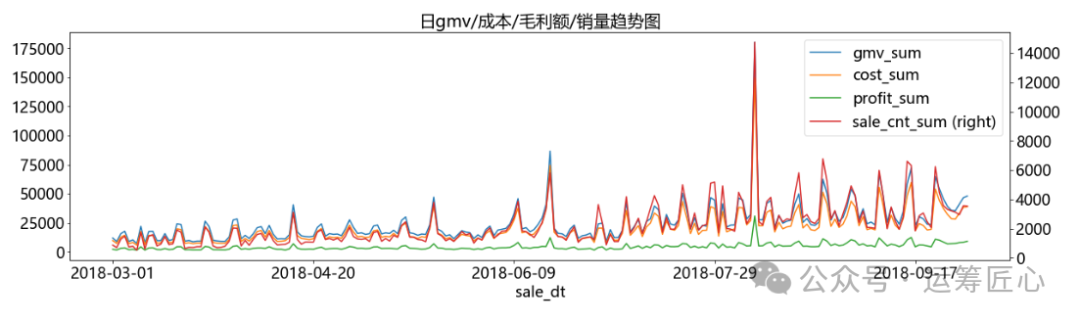

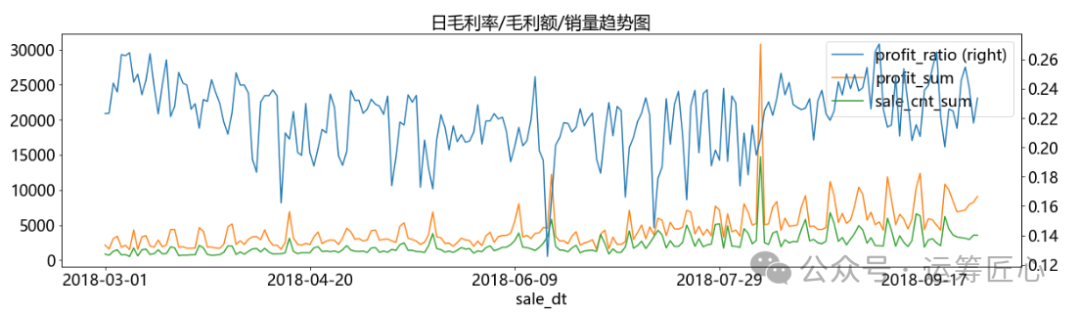
图片图片图片我们发现：

  • GMV、利润额与销量呈强正相关，销量越高，GMV、利润额越高。

  • 利润率与销量、利润额相关性不明显，有时利润率很低，但利润额很高；有时相反。这说明“降价促销”是存在赚钱的可能性的。

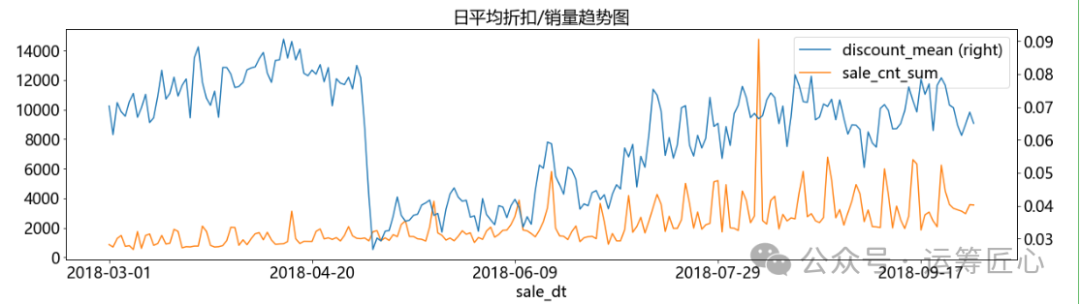
  • 折扣率与销量呈正相关，趋势相同，但并不是折扣率越高一定是销量越高，如：商家在5.4后大幅调低整体折扣，但销量不降反升。这说明精细化定价是可行的，在合理的折扣区间制定高销的价格，增加GMV和利润。

2）品维度

统计各级品类/sku下子品类宽度（子品类个数）、sku宽度（个数）、sku总销量、sku价格等信息，画出分布图。由于篇幅有限，这里只列出sku维度下相关代码。

# 各sku历史价格数/总销量/日售价均值/售卖天数/日均销量分布  
ret_df = IOR_DP.group_agg(df=data_df,   grp_cols=['sku_id', 'sku_name'],   agg_dict={'sale_cnt': 'sum', 'sale_prc':  ['nunique', 'max', 'min', 'mean'],   'ori_prc': ['nunique', 'max', 'min', 'mean'], 'cost_prc':  ['nunique', 'max', 'min', 'mean']},  sort_dict={'sale_cnt_sum': 'desc'})  
ret_df = ret_df.head(50)  
pic1 = ret_df.plot(x='sku_name', y=['sale_prc_nunique', 'sale_cnt_sum'],  secondary_y= 'sale_cnt_sum', title = 'Top50总销量的sku的历史价格数/总销量(降序)分布',  kind='bar', figsize=(20, 5), fontsize=18)  top_sku = ret_df['sku_name']  
ret_df = IOR_DP.group_agg(df=data_df, grp_cols=['sku_id', 'sku_name'], agg_dict={ 'sale_dt': 'count',  'sale_cnt': 'mean'},  sort_dict={'sale_cnt_mean': 'desc'})  
ret_df = pd.merge(left=ret_df, right=top_sku, how='inner', on=['sku_name'])  
pic2 = ret_df.plot(x='sku_name', y=['sale_dt_count', 'sale_cnt_mean'], secondary_y= 'sale_cnt_mean',  title = 'Top50总销量的sku的历史售卖天数/日均销量(降序)分布',  kind='bar', figsize=(20, 5), fontsize=18)  ret_df = IOR_DP.group_agg(df=data_df,   grp_cols=['sale_dt', 'sku_name'],   agg_dict={ 'sale_prc': 'mean'},  sort_dict={'sale_dt': 'asc'})  
ret_df = pd.merge(left=ret_df, right=top_sku, how='inner', on=['sku_name'])  
ret_df = ret_df.pivot_table(values='sale_prc_mean', index='sale_dt', columns='sku_name').reset_index()  
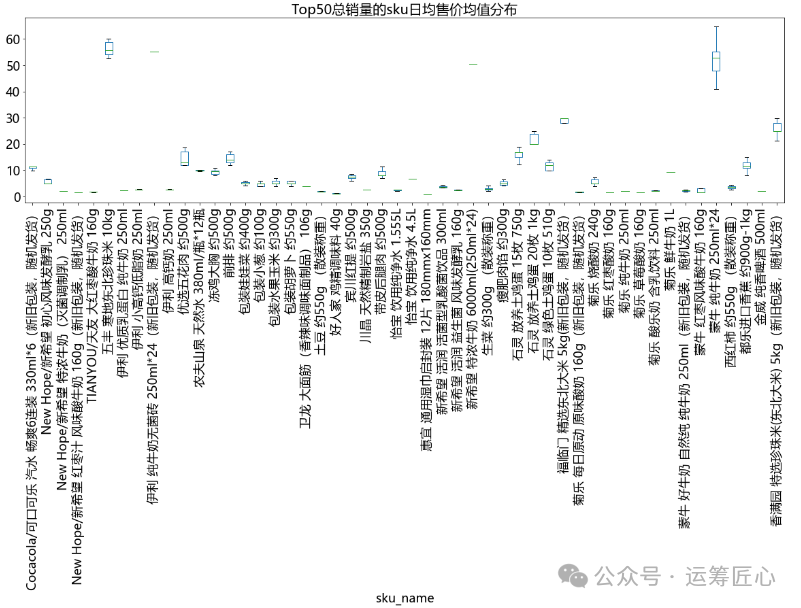
pic3 = ret_df.plot(title = 'Top50总销量的sku日均售价均值分布', kind='box', rot=90, showfliers=False, figsize=(20, 5), fontsize=18)  plt.xlabel('sku_name')  
plt.show([pic1, pic2, pic3])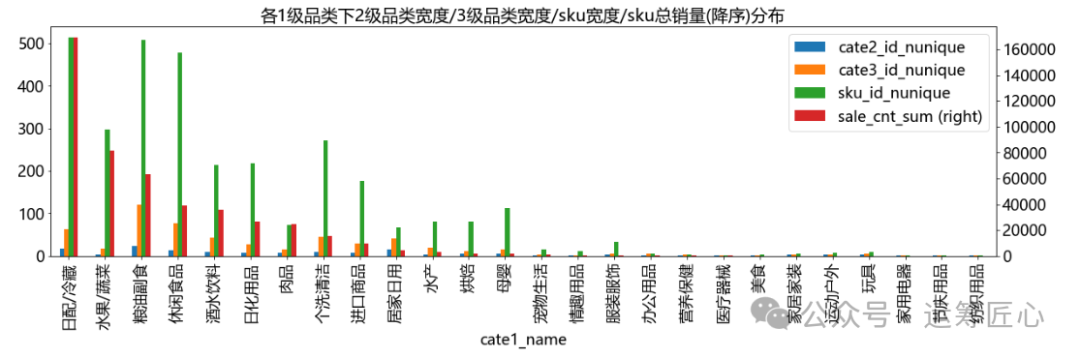

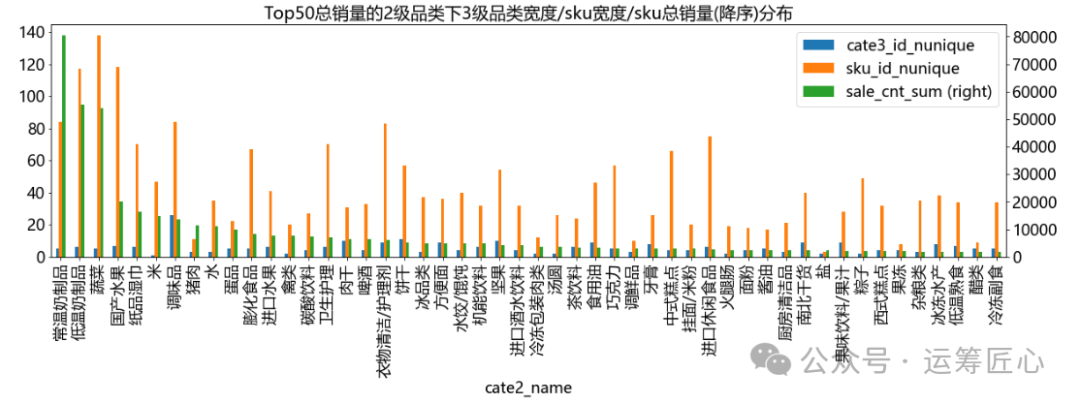
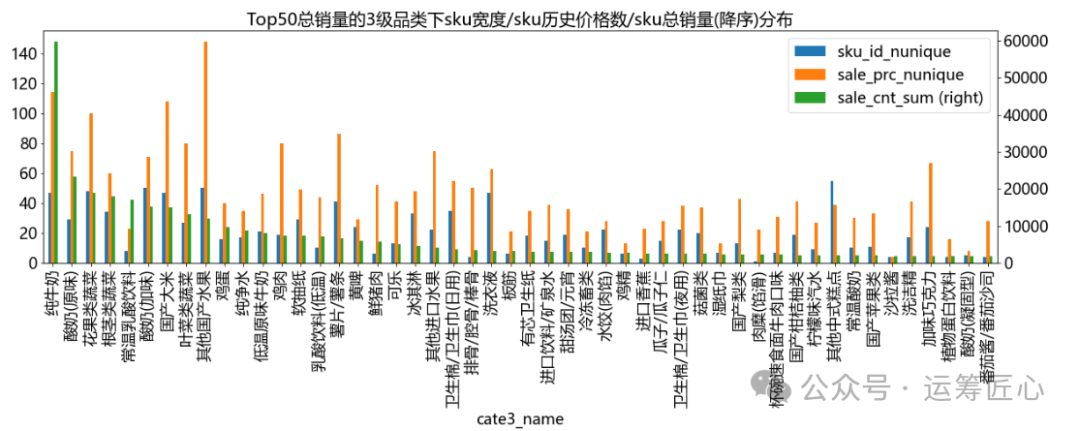
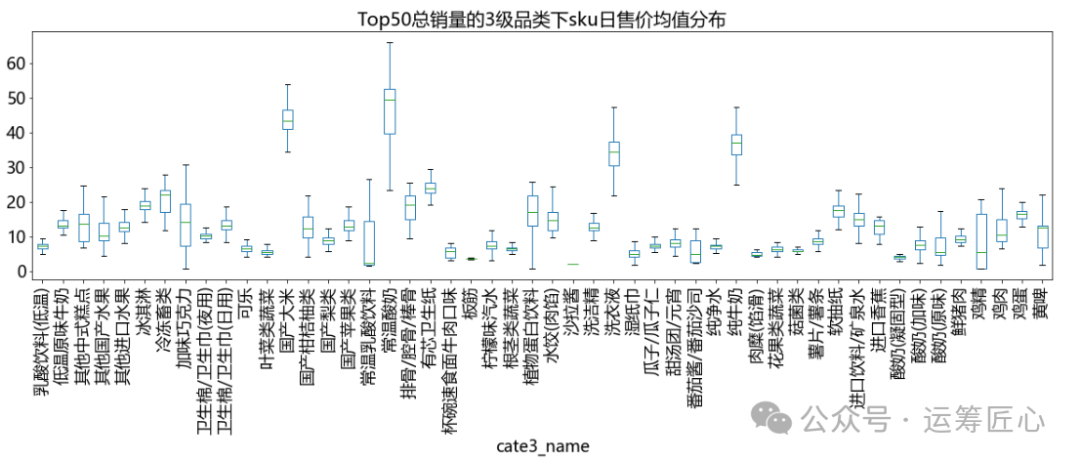
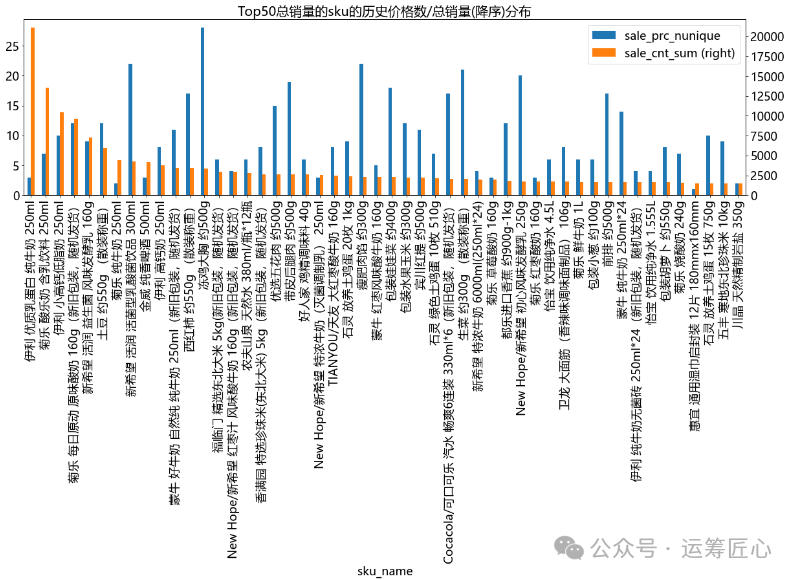
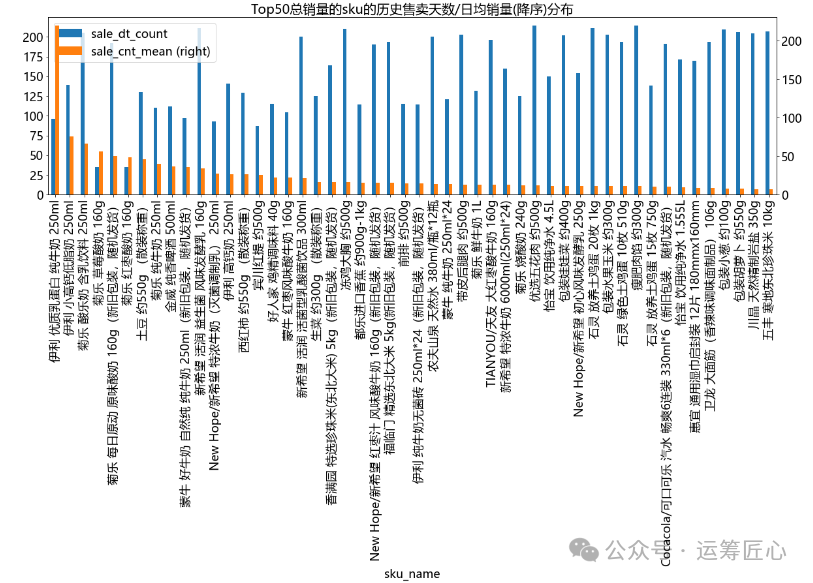
图片图片图片图片图片图片图片我们发现：

  • 不同品类下的子品类和sku数量差异较大。以3级品类下sku数为例：最少1个，最多63个，中位值3个；

  • 不同sku的价格带不同。以售价均值为例：最小0.8元，最大1100元，中位值13.80元。这说明定价时每个sku的价格区间需要精细化制定。

3）价格维度

统计不同价格区间下sku宽度、总销量、总gmv、总成本、总毛利，画出分布图。

ret_df = data_df[['sale_prc', 'sku_name', 'sale_cnt', 'gmv', 'cost', 'profit']]  
ret_df['sale_prc_range'] = pd.cut(ret_df['sale_prc'], bins)  
ret_df = IOR_DP.group_agg(df=ret_df,   grp_cols=['sale_prc_range'],   agg_dict={'sku_name': 'nunique', 'sale_cnt': 'sum', 'gmv': 'sum', 'cost': 'sum', 'profit': 'sum'},  sort_dict={'sale_prc_range': 'asc'})  
ret_df = ret_df.rename(columns={'sku_name_nunique':'sku_cnt'})  
pic1 = ret_df.plot(x='sale_prc_range', y=['sku_cnt', 'sale_cnt_sum', 'gmv_sum', 'cost_sum', 'profit_sum'],   secondary_y = 'sku_cnt', kind='bar', title='不同价格区间下sku宽度/销量/GMV/成本/毛利分布',   figsize=(20, 5), fontsize=18)  
plt.show(pic1)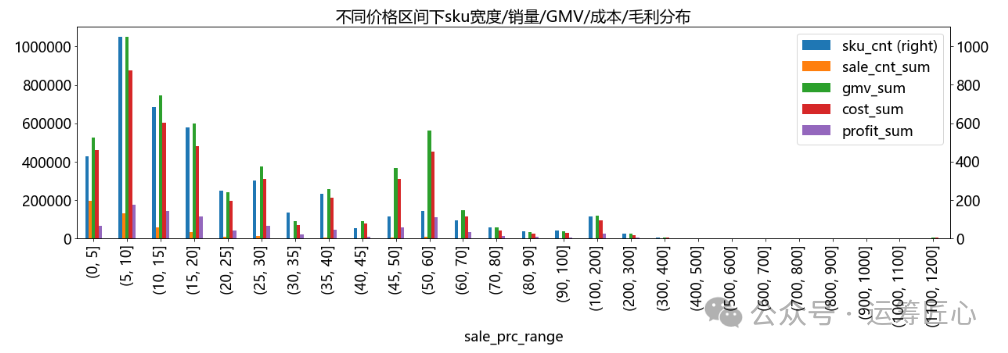

图片我们发现，绝大部分sku的价格分布在20元以下，5-10元区间的sku占比最多。

4）数量维度

分别统计不同历史售卖天数和不同历史价格数下的sku宽度分布，画出分布图。

# 不同历史售卖天数下sku宽度分布  
ret_df = IOR_DP.group_agg(df=data_df, grp_cols=['sku_id', 'sku_name'], agg_dict={ 'sale_dt': 'count'})  
ret_df = IOR_DP.group_agg(df=ret_df, grp_cols=['sale_dt_count'], agg_dict={ 'sku_id': 'count'}, sort_dict={'sale_dt_count':'asc'})  
ret_df = ret_df.head(70)  
pic1 = ret_df.plot(x='sale_dt_count', y='sku_id_count', kind='bar',   title='不同历史售卖天数下sku宽度分布', figsize=(20, 5), fontsize=18)  
plt.show(pic1)  
# 不同历史价格数下sku宽度分布  
ret_df = IOR_DP.group_agg(df=data_df, grp_cols=['sku_id', 'sku_name'], agg_dict={ 'sale_prc': 'nunique'})  
ret_df = IOR_DP.group_agg(df=ret_df, grp_cols=['sale_prc_nunique'], agg_dict={ 'sku_id': 'count'}, sort_dict={'sale_prc_nunique':'asc'})  
pic1 = ret_df.plot(x='sale_prc_nunique', y='sku_id_count', kind='bar',   title='不同历史价格数下sku宽度分布', figsize=(20, 5), fontsize=18)  
plt.show(pic1)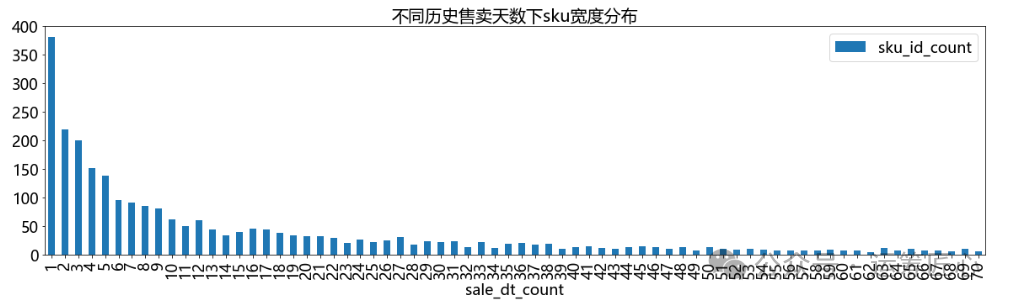

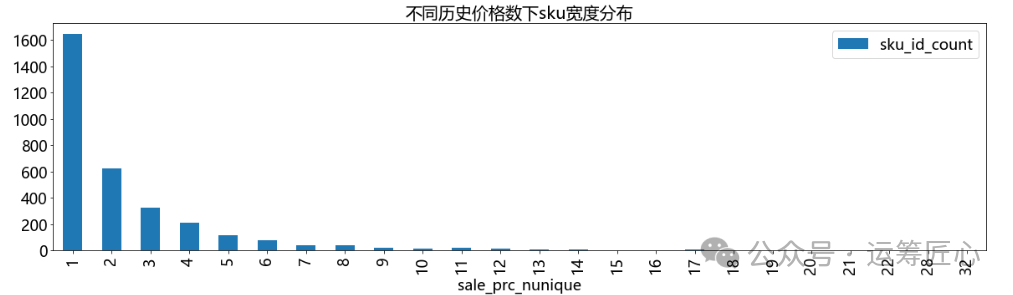
图片图片

我们发现：不同sku的历史价格数量不同，绝大部分的sku历史价格数量只有1个。针对该现象需要进一步分析，有2种可能：

  • 这部分商品为低价格弹性商品，即价格改变不会引起销量的变化；

  • 这部分商品是高价格弹性商品，但商家未进行太多的促销价格尝试，这会导致这部分商品精细化定价时样本不足，需要思考如何解决该问题。

03 相关分析

针对1级品类/2级品类/3级品类/sku，分别计算售价/折扣比例/折扣额与日销量间的pearson相关性系数，画出分布图。

1）1级品类

cate_level = 'cate1_name'  
corr_df = cal_corr_by_cate(data_df, cate_level = cate_level)  
feature_cols = list(corr_df.columns)[1:]  
corr_df = corr_df.sort_values(by=feature_cols, ascending=[True] * len(feature_cols))  
pic1 = corr_df.plot(x=cate_level, y=feature_cols, title = '1级品类售价/折扣比例/折扣额与日销量相关性',  kind='bar', figsize=(20, 5), fontsize=18)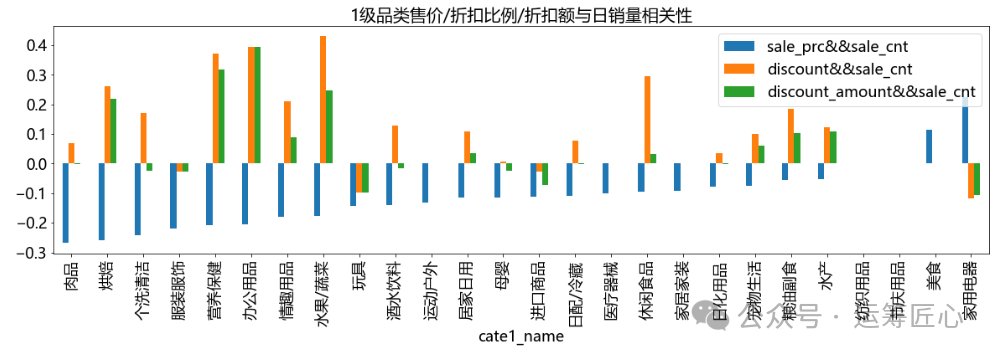

图片

2）2级品类

cate_level = 'cate2_name'  
ret_df = IOR_DP.group_agg(df=data_df,   grp_cols=[cate_level],   agg_dict={'sale_cnt': 'sum'},  sort_dict={'sale_cnt_sum': 'desc'})  
ret_df = ret_df.head(50)  
corr_df = cal_corr_by_cate(data_df, cate_level = cate_level)  
corr_df = pd.merge(left=ret_df, right=corr_df, how='inner', on=[cate_level])  
feature_cols = list(corr_df.columns)[2:]  
corr_df = corr_df.sort_values(by=feature_cols, ascending=[True] * len(feature_cols))  
pic1 = corr_df.plot(x=cate_level, y=feature_cols, title = 'Top50销量的2级品类售价/折扣比例/折扣额与日销量相关性',  kind='bar', figsize=(20, 5), fontsize=18)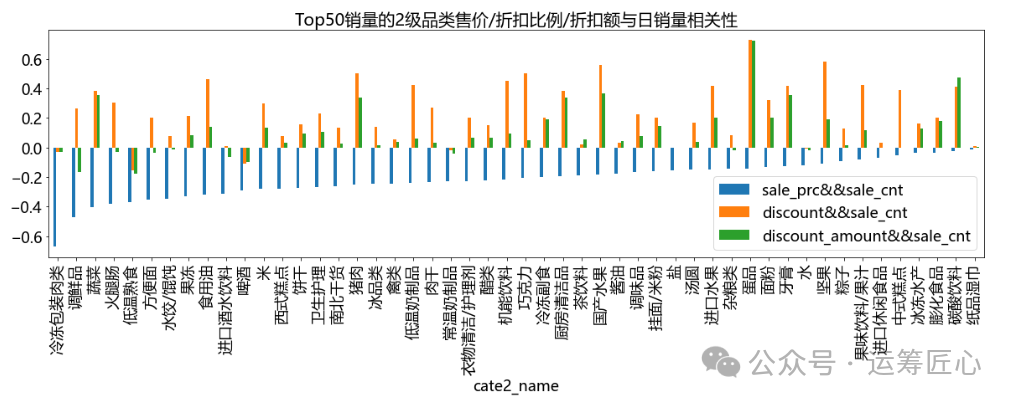

图片

3）3级品类

cate_level = 'cate3_name'  
ret_df = IOR_DP.group_agg(df=data_df,   grp_cols=[cate_level],   agg_dict={'sale_cnt': 'sum'},  sort_dict={'sale_cnt_sum': 'desc'})  
ret_df = ret_df.head(50)  
corr_df = cal_corr_by_cate(data_df, cate_level = cate_level)  
corr_df = pd.merge(left=ret_df, right=corr_df, how='inner', on=[cate_level])  
feature_cols = list(corr_df.columns)[2:]  
corr_df = corr_df.sort_values(by=feature_cols, ascending=[True] * len(feature_cols))  
pic1 = corr_df.plot(x=cate_level, y=feature_cols, title = 'Top50销量的3级品类售价/折扣比例/折扣额与日销量相关性',  kind='bar', figsize=(20, 5), fontsize=18)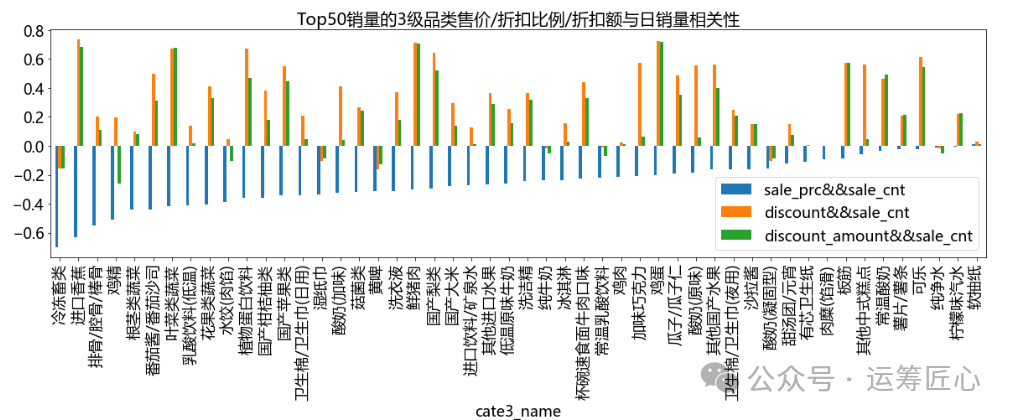

图片

4）sku

cate_level = 'sku_name'  
ret_df = IOR_DP.group_agg(df=data_df,   grp_cols=[cate_level],   agg_dict={'sale_cnt': 'sum'},  sort_dict={'sale_cnt_sum': 'desc'})  
ret_df = ret_df.head(50)  
corr_df = cal_corr_by_cate(data_df, cate_level = cate_level)  
corr_df = pd.merge(left=ret_df, right=corr_df, how='inner', on=[cate_level])  
feature_cols = list(corr_df.columns)[2:]  
corr_df = corr_df.sort_values(by=feature_cols, ascending=[True] * len(feature_cols))  
pic1 = corr_df.plot(x=cate_level, y=feature_cols, title = 'Top50销量的sku售价/折扣比例/折扣额与日销量相关性',  kind='bar', figsize=(20, 5), fontsize=18)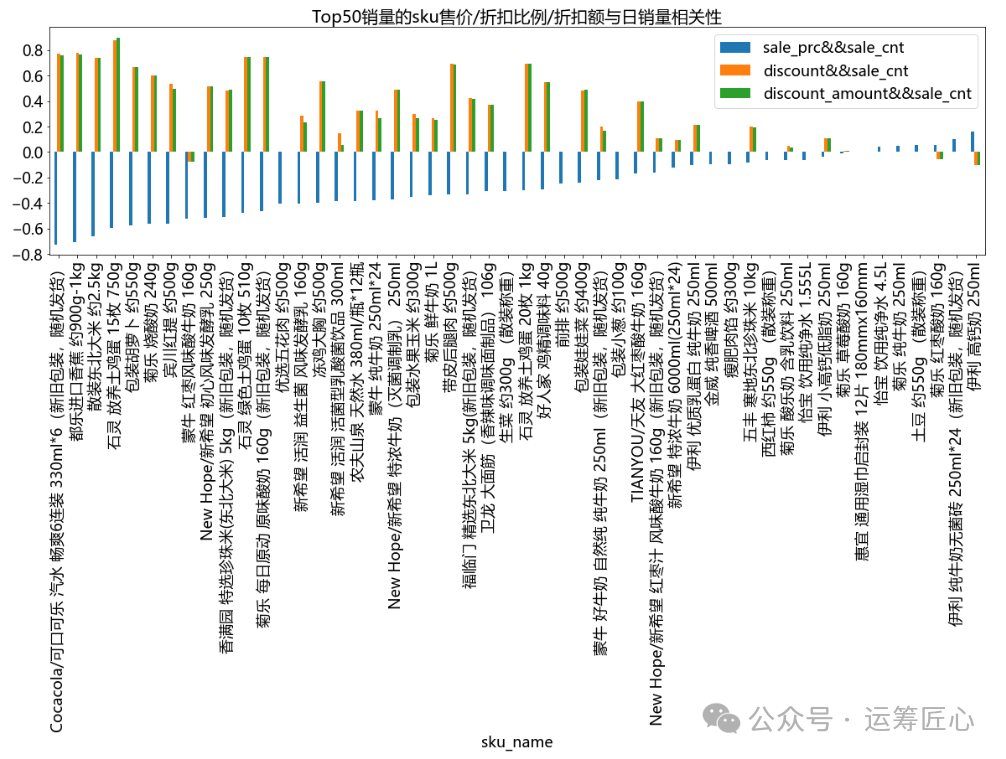

图片

我们发现，不同品类/sku的售价/折扣比例/折扣额与日销量间相关性差异极大。如：

  • 对于可口可乐、散装东北大米等长保质期商品来说，售价越低/折扣比例越大/折扣额越大，销量越高。可能是因为该类商品可以囤货。

  • 对于进口香蕉、土鸡蛋等生鲜品来说，售价越低/折扣比例越大/折扣额越大，销量越高。可能是因为该类商品日常消耗较快。

  • 对于红枣风味酸牛奶等短保质期商品来说，售价越低，销量越高；折扣比例/折扣额和销量呈负相关，但相关性不大。可能是因为该类商品一旦打折就意味着临近保质期，大家不愿意购买。

  • 对于伊利高钙奶等高品质商品来说，则售价越高，销量越高，但相关性不大。可能是因为该类商品价格越高品质越佳。

因此，在促销定价时，需要根据不同的sku制定不同的定价策略。

04 聚类分析

根据03节计算出来的3级品类平均售价/折扣比例/折扣额与日销量间的相关性系数，对3级品类进行聚类，画出聚类图。

cate_level = 'cate3_name'  
corr_df = cal_corr_by_cate(data_df, cate_level = cate_level)  
n_clusters = 4  
x_cols = list(corr_df.columns)[1:]  
x_df = corr_df[x_cols]  
from sklearn.cluster import KMeans#导入聚类模型  
model1=KMeans(n_clusters=n_clusters, n_init=1000).fit(x_df)#聚成3类传入自变量  
model1.labels_.size  
corr_df['label']=model1.labels_  # 3D  
fig =plt.figure(figsize=(20, 10))  
ax = Axes3D(fig)  
pic2 = ax.scatter(xs=corr_df['sale_prc&&sale_cnt'], ys=corr_df['discount&&sale_cnt'], cmap='jet',  zs=corr_df['discount_amount&&sale_cnt'], c = corr_df['label'], alpha=1)  
ax.set_xlabel('sale_prc&&sale_cnt', color='r')  
ax.set_ylabel('discount&&sale_cnt', color='g')  
ax.set_zlabel('discount_amount&&sale_cnt', color='b')  
plt.title('售价/折扣比例/折扣额与日销量相关性分类图')  
plt.show(pic2)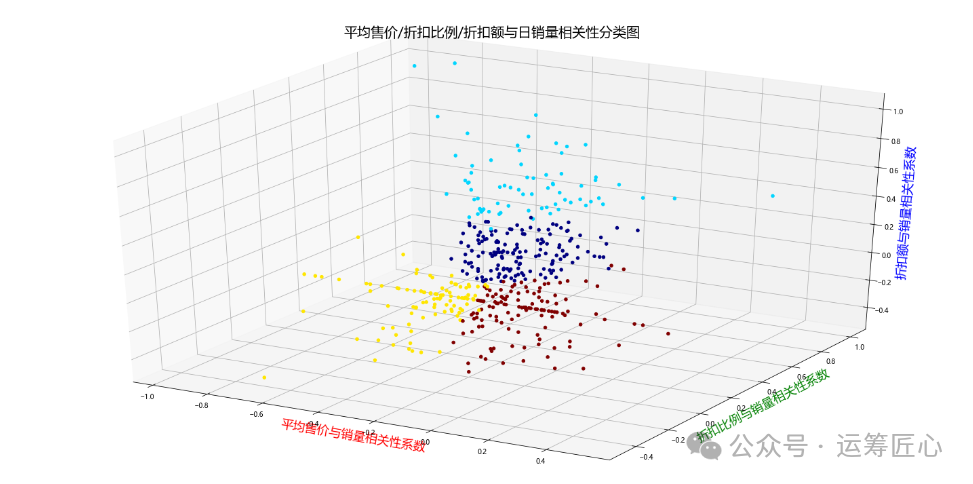

图片图片经过实验我们发现，聚4类即可将样本较好的分开，聚类结果也符合业务常识。详情如下：

  • label=0分类的3级品类，平均售价与日销量弱负相关，折扣比例/折扣额与日销量弱正相关，多为保质期较长，购物频次一般的品类，如：‘一次性内裤’, ‘丸类’, ‘乌龙茶饮品’, ‘冰冻贝类’, '冰淇淋’等。

  • label=1分类的3级品类，平均售价与日销量强负相关，折扣比例/折扣额与日销量强正相关，多为保质期较短，购物频次较高的品类，如：‘中式点心’, ‘低温加味牛奶’, ‘可乐’, ‘叶菜类蔬菜’, ‘吐司类’, ‘国产季节性水果’, ‘国产梨类’ '婴儿卫生用品’等。

  • label=2分类的3级品类，平均售价与日销量强负相关，折扣比例/折扣额与日销量强不相关，多为购物频次一般，但平时很少有折扣促销的品类，如：‘其他冲饮粉’, ‘其他肉干’, ‘其他进口洋酒’, ‘名酒’, '味精’等。

  • label=3分类的3级品类，平均售价/折扣比例/折扣额与日销量强均不相关，多为购物频次较低，平时也很少有折扣促销的品类，如：‘LED灯泡’, ‘一口酥/酥饼’, ‘一次性卫生筷’, ‘一次性塑料口杯’, ‘一次性手套’, ‘一次性纸口杯’, '一次性纸碗’等。

05 核心结论

综上诉说，我们利用数据挖掘技术，从各个维度较为全面的分析了数据的全貌，并深度挖掘了价格/折扣和销量之间的关系。最终，我们得到了一个核心结论：不同的sku的价格/折扣与销量之间的关系不同，促销定价做的越精细，效果越好。而精细化正是算法相较人工的优势所在。

06 小结

第一篇（业务问题拆解）：我们把一个实际的促销定价问题拆解成了一系列的数学问题。

第二篇（数据预处理生成）：我们选择了一份公开的促销定价数据集，将其加工成了可分析求解的数据。

本篇（数据挖掘分析）：我们对数据进行了全方位的挖掘和分析，介绍了数据挖掘分析和可视化方法。敬请期待~~~

下一篇（价格弹性模型）：我们将介绍如何利用价格弹性模型量化商品价格与销量的关系。敬请期待~~~

参考文献

  1. Hua J, Yan L, Xu H,et al. Markdowns in E-Commerce Fresh Retail: A Counterfactual Prediction and Multi-Period Optimization Approach[J]. arxiv, 2021.(https://arxiv.org/pdf/2105.08313.pdf)

  2. Kui Zhao, Junhao Hua, Ling Yan, et al. A Unified Framework for Marketing Budget Allocation[J]. arxiv, 20.(https://arxiv.org/pdf/1902.01128.pdf)

  3. 用相关系数进行Kmeans聚类，利用利润率、打折率、销售额、毛利润得到商品价格弹性标签，建立价格折扣力度模型(https://blog.csdn.net/weixin_45934622/article/details/114382037)

  4. 2019全国大学生数学建模竞赛讲评：“薄利多销”分析(https://dxs.moe.gov.cn/zx/a/hd_sxjm_sxjmstjp_2019sxjmstjp/210604/1699445.shtml)

  5. 策略算法工程师之路-基于线性规划的简单价格优化模型(https://zhuanlan.zhihu.com/p/145192690)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/268733.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

C++学习笔记:set和map

C++学习笔记:set和map

set和map set什么是setset的使用 关联式容器键值对 map什么是mapmap的使用map的插入方式常用功能map[] 的灵活使用 set 什么是set set是STL中一个底层为二叉搜索树来实现的容器 若要使用set需要包含头文件 #include<set>set中的元素具有唯一性(因此可以用set去重)若用…
阅读更多...
Docker之数据卷自定义镜像

Docker之数据卷自定义镜像

文章目录 前言一、数据卷二、自定义镜像 前言 Docker提供了一个持久化存储数据的机制&#xff0c;与容器生命周期分离&#xff0c;从而带来一系列好处&#xff1a; 总的来说Docker 数据卷提供了一种灵活、持久、可共享的存储机制&#xff0c;使得容器化应用在数据管理方面更加…
阅读更多...
Newtonsoft.Json

Newtonsoft.Json

目录 引言 1、简单使用 1.1、官方案例 1.2、JsonConvert 2、特性 2.1、默认模式[JsonObject(MemberSerialization.OptIn/OptOut)] 2.2、序列化为集合JsonArrayAttribute/JsonDictionaryAttribute 2.3、序列化该元素JsonProperty 2.4、忽略元素JsonIgnoreAttribute 2.5、…
阅读更多...
超全Chat GPT论文修改指令

超全Chat GPT论文修改指令

文献综述指令润色修改指令论文选题指令论文大指令研究理论指令论文致谢指令参考文献指令论文润色整体逻辑论文整体优化提问指令 1&#xff0e;文献综述指令 请你帮我写一份关于&#xff08;研究主题&#xff09;的文献综述。我的论文选题方向是 XXXX &#xff0c;我已经找到了…
阅读更多...
WordPress上传图片错误:不是合法的JSON响应

WordPress上传图片错误:不是合法的JSON响应

最近在进行WordPress迁移至新服务器的过程中&#xff0c;遭遇到一个棘手的问题&#xff0c;即在编辑文章并上传图片时&#xff0c;不断遭遇“此响应不是合法的JSON响应”的错误。经过多次验证和搜索&#xff0c;最终确定问题的根本原因并不在于禁用 Gutenberg 编辑器或安装经典…
阅读更多...
uniapp从入门到精通（全网保姆式教程）~ 别再说你不会开发小程序了

uniapp从入门到精通（全网保姆式教程）~ 别再说你不会开发小程序了

目录 一、介绍 二、环境搭建&#xff08;hello world&#xff09; 2.1 下载HBuilderX 2.2 下载微信开发者工具 2.3 创建uniapp项目 2.4 在浏览器运行 2.5 在微信开发者工具运行 2.6 在手机上运行 三、项目基本目录结构 四、开发规范概述 五、全局配置文件&#xff0…
阅读更多...
如何在Node.js中使用定时器

如何在Node.js中使用定时器

在Node.js中使用定时器是一项常见且重要的任务&#xff0c;特别是在需要执行定时任务或者轮询操作的情况下。Node.js提供了多种方式来实现定时器功能&#xff0c;包括setTimeout、setInterval和setImmediate等方法。本篇博客将介绍如何在Node.js中使用这些定时器&#xff0c;并…
阅读更多...
Kubernetes的Sevice管理

Kubernetes的Sevice管理

服务原理: 所有服务都是根据这个服务衍生或者变化出来,根服务---- 服务感知后端靠标签 slelector 标签选择器 kubectl label pods web1 appweb kubectl cluter-info dump | grep -i service-cluster-ip-range 服务ip取值范围 Service 管理: 创建服务: --- kind: Serv…
阅读更多...
python复盘（1）

python复盘（1）

1、变量名的命名规则 #3、变量名的命名规则&#xff1a;可以用中文作为变量名&#xff1b;其他和go语言一样 # 变量名可以用数字、字母、下划线组成&#xff0c;但是数字不能作为开头 # 变量名不能使用空格&#xff0c;不能使用函数名或关键字 # 变量名最好能表示出他的作用2、…
阅读更多...
大模型（LLM）的量化技术Quantization原理学习

大模型（LLM）的量化技术Quantization原理学习

在自然语言处理领域&#xff0c;大型语言模型&#xff08;LLM&#xff09;在自然语言处理领域的应用越来越广泛。然而&#xff0c;随着模型规模的增大&#xff0c;计算和存储资源的需求也急剧增加。为了降低计算和存储开销&#xff0c;同时保持模型的性能&#xff0c;LLM大模型…
阅读更多...
OpenGL 实现色温、色调、亮度、对比度、饱和度、高光

OpenGL 实现色温、色调、亮度、对比度、饱和度、高光

1.简介 色温&#xff1a;简单理解是色彩的温度&#xff0c;越低越冷如蓝色&#xff0c;约高越暖如红色。 亮度&#xff1a;增加就是给图片所有色彩加白色&#xff0c;减少加黑色。注意是只加黑白两种颜色&#xff0c;不然容易跟纯度弄混。 对比度&#xff1a;增加就是让白的…
阅读更多...
2023人机交互期末复习

2023人机交互期末复习

考试题型及分值分布 1、选择题&#xff08;10题、20分&#xff09; 2、填空题&#xff08;10题、20分&#xff09; 3、判断题&#xff08;可选、5题、10分&#xff09; 4、解答题&#xff08;5~6题、30分&#xff09; 5、分析计算题&#xff08;1~2题、20分&#xff09; 注意&…
阅读更多...
如何做代币分析：以 LEO 币为例

如何做代币分析：以 LEO 币为例

作者&#xff1a; lesleyfootprint.network 编译&#xff1a;cicifootprint.network 数据源&#xff1a;LEO 代币仪表板 &#xff08;仅包括以太坊数据&#xff09; 在加密货币和数字资产领域&#xff0c;代币分析起着至关重要的作用。代币分析指的是深入研究与代币相关的数…
阅读更多...
uniapp实战:父子组件传参之子组件数量动态变化

uniapp实战:父子组件传参之子组件数量动态变化

需求说明 现有的设置单元列表,每个带有虚线加号的可以看做是一组设置单元,点击加号可以添加一组设置单元.点击设置单元右上角可以删除对应的设置单元. 实现思路说明 利用数组元素添加或是删除的方式实现页面数量动态变化.由于每个设置单元内容都相同所以单独封装了一个子组件.…
阅读更多...
LeetCode206题：反转链表（python3）

LeetCode206题：反转链表（python3）

采用递归 class Solution:def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:cur headpre Nonewhile cur:temp cur.next # 保存下一轮循环的节点cur.next pre # 将当前节点 cur 的指针指向上一个节点 prepre curcur tempreturn pre
阅读更多...
uni-app 微信小程序：启用组件按需注入

uni-app 微信小程序：启用组件按需注入

原文地址&#xff1a;uni-app 微信小程序&#xff1a;启用组件按需注入 - 掘金 只需添加以下代码"lazyCodeLoading": "requiredComponents"
阅读更多...
卷积神经网络(CNN)原理与实现

卷积神经网络(CNN)原理与实现

卷积神经网络(CNN) 卷积神经网络原理卷积神经网络的数学推导卷积层反向传播算法数学推导卷积层实现代码 卷积神经网络(CNN) 卷积神经网络原理 卷积神经网络是一种用于图像、语音、自然语言等数据的深度学习模型&#xff0c;其核心思想是使用卷积操作提取输入数据的特征&…
阅读更多...
Mysql中的事务

Mysql中的事务

什么是事务&#xff1a; 多条sql语句&#xff0c;要么全部成功&#xff0c;要么全部失败。 事务的特性&#xff1a; 1&#xff1a;原子性(Atomic)&#xff1a; 组成一个事务的多个数据库操作是一个不可分割的原子单元&#xff0c;只有所有操作都成功&#xff0c;整个事务才会…
阅读更多...
算法学习系列（三十八）：超级源点问题

算法学习系列（三十八）：超级源点问题

目录 引言一、题目描述二、解题思路三、示例代码 引言 关于最短路问题不论是竞赛、找工作、笔试面试、机试考的都是挺多的&#xff0c;所以还是非常的重要&#xff0c;最重要的就是模板首先背过&#xff0c;然后通过刷题见各种各样的题&#xff0c;具体难点就是如何建图、怎么…
阅读更多...
【牛客面试必刷TOP101】Day25.BM38 在二叉树中找到两个节点的最近公共祖先和BM40 重建二叉树

【牛客面试必刷TOP101】Day25.BM38 在二叉树中找到两个节点的最近公共祖先和BM40 重建二叉树

作者简介&#xff1a;大家好&#xff0c;我是未央&#xff1b; 博客首页&#xff1a;未央.303 系列专栏&#xff1a;牛客面试必刷TOP101 每日一句&#xff1a;人的一生&#xff0c;可以有所作为的时机只有一次&#xff0c;那就是现在&#xff01;&#xff01;&#xff01;&…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023