归并算法详细解析

归并排序

1945年，约翰·冯·诺依曼（John von Neumann）发明了归并排序，这是典型的分治算法的应用。归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

基本思想

归并排序是使用分治算法，就是把序列分成长度相同的两个子序列，当无法继续往下分时（也就是每个子序列中只有一个数据时），就对子序列进行归并。归并指的是把两个排好序的子序列合并成一个有序序列。该操作会一直重复执行，直到所有子序列都归并为一个整体为止。

图形演示

为方便查看，我们用不同高度来表示不同的数字大小
在这里插入图片描述

首先我们把序列逐层对半分割

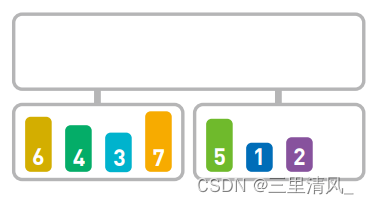
直至不能再分割为止
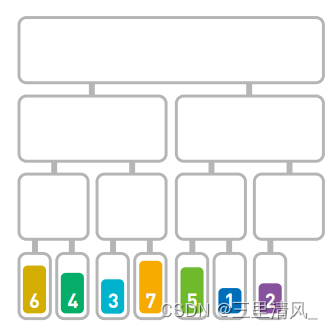
在这里插入图片描述

分割完毕，接下来对每组元素进行合并；合并时需要将数字按照从小到大的顺序排列：

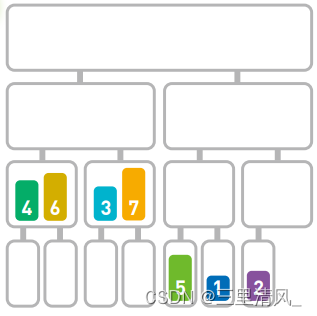
每次合并时比较两个子序列的首位数字。当合并有多个数字的子序列时，要先比较首位数字，再移动较小的数字：由于3<4,所以要先移动3，接下来再比较4和7；4<7，所以移动4，再比较6和7…如此往复，左半个序列就排序好啦
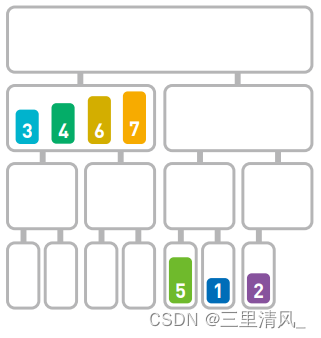
在这里插入图片描述

右边也是如此，直至所有的数字都合并为一个整体为止
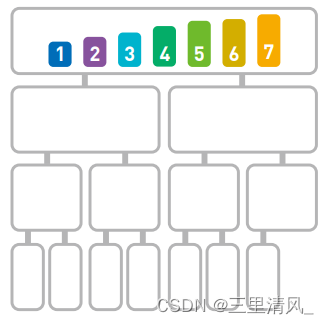
在这里插入图片描述

合并完成，序列的排序也就完成了

时间复杂度分析

归并排序中，分割序列所花费的时间不算在运行时间内（可以当作序列本来就是分割好的）。在合并两个已排好序的子序列时，只需重复比较首位数据的大小，然后移动较小的数据，因此只需花费和两个子序列的长度相应的运行时间。也就是说，完成一行归并所需的运行时间取决于这一行的数据量。看一下上面的图便能得知，无论哪一行都是 n 个数据，所以每行的运行时间都为 O(n)。而将长度为 n 的序列对半分割直到只有一个数据为止时，可以分成 log2n 行，因此，总共有 log2n 行。也就是说，总的运行时间为 O(nlogn)，这与前面讲到的堆排序相同。

代码实现

迭代法

public static void merge_sort(int[] arr) {int len = arr.length;int[] result = new int[len];int block, start;for(block = 1; block < len*2; block *= 2) {for(start = 0; start <len; start += 2 * block) {int low = start;int mid = (start + block) < len ? (start + block) : len;int high = (start + 2 * block) < len ? (start + 2 * block) : len;int start1 = low, end1 = mid;int start2 = mid, end2 = high;while (start1 < end1 && start2 < end2) {result[low++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];}while(start1 < end1) {result[low++] = arr[start1++];}while(start2 < end2) {result[low++] = arr[start2++];}}int[] temp = arr;arr = result;result = temp;}result = arr;       
}

递归法

static void merge_sort_recursive(int[] arr, int[] result, int start, int end) {if (start >= end)return;int len = end - start, mid = (len >> 1) + start;int start1 = start, end1 = mid;int start2 = mid + 1, end2 = end;merge_sort_recursive(arr, result, start1, end1);merge_sort_recursive(arr, result, start2, end2);int k = start;while (start1 <= end1 && start2 <= end2)result[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];while (start1 <= end1)result[k++] = arr[start1++];while (start2 <= end2)result[k++] = arr[start2++];for (k = start; k <= end; k++)arr[k] = result[k];
}public static void merge_sort(int[] arr) {int len = arr.length;int[] result = new int[len];merge_sort_recursive(arr, result, 0, len - 1);
}