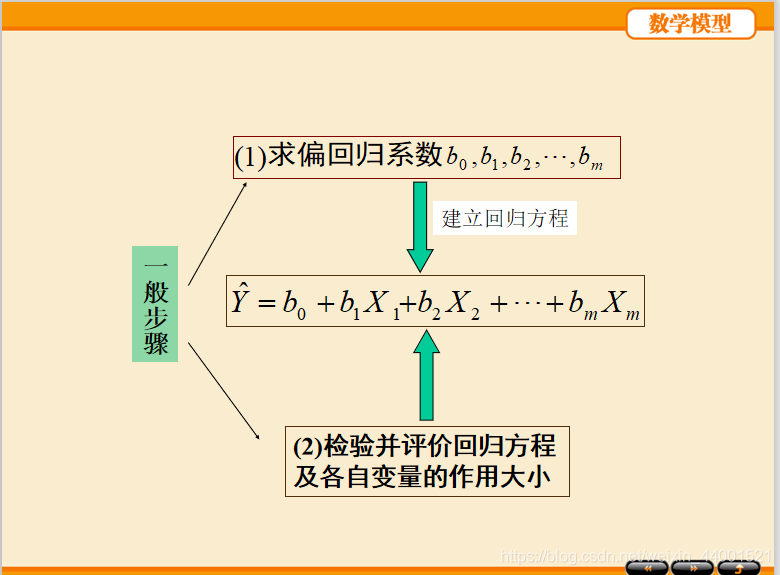
1.单因素一元方差分析的方法和案例：
例子：

案例的代码：
X=[533 580 525 600 570 650 500; %因数I [A,F]实验组+CK标准
565 600 500 615 575 661 510;
525 575 510 590 565 643 513];
group={‘A’,‘B’,‘C’,‘D’,‘E’,‘F’,‘CK’};
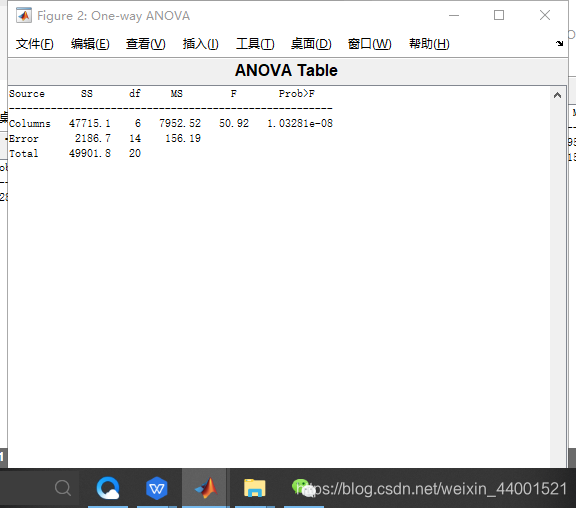
[p ,table,stats]=anova1(X,group) %p接近于0则不接受零假设，即各列均值的差异式由实验因素造成
[c,m,h,gnames]=multcompare(stats)
c =multcompare(stats)

Source表示方差来源（谁的方差），这里的方差来源包括Groups（组间），Error（组内），Total（总计）；
SS（Sum of squares）表示平方和
df（Degree of freedom）表示自由度
MS（Mean squares）表示均方差
F表示F值（F统计量），F值等于组间均方和组内均方的比值，它反映的是随机误差作用的大小。
Prob>F表示p值
这里需要引出两个小问题：第一个小问题是F值怎么使用，第二个小问题是p值和F值的关系是什么？
率先普及一下p值和F值之间的关系：
F实际值>F查表值，则p<=0.05
F实际值<F查表值，则p>0.05
参考：
https://www.cnblogs.com/hdu-zsk/p/6293721.html
②双因素一元方差分析的方法和案例：

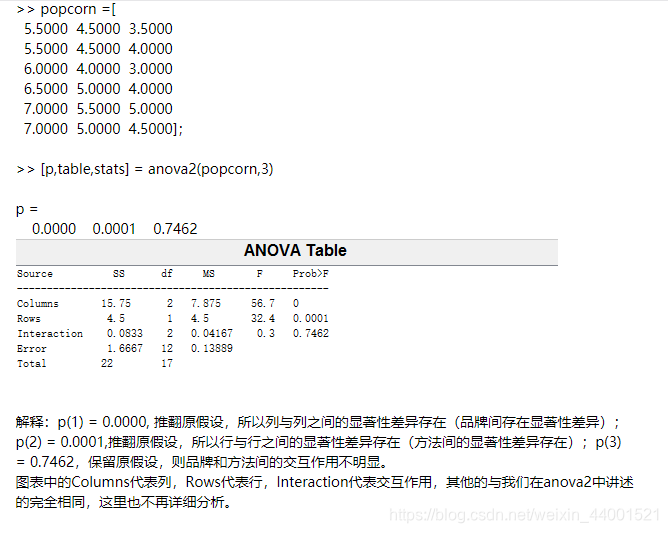
% 例子
%列：A品种 B密度A1B1 ;A2B1 ;A3B1;A1B2;A2B2;A3B3;
X=[40 46 47;%I A1B1 A2B1 A3B1
38 42 43 ;%II A1B1 A2B1 A3B1
42 44 45 ;%III A1B1 A2B1 A3B1
42 48 50;%I A1B2 A2B2 A3B2
44 47 48;%II A1B2 A2B2 A3B2
45 46 49];%III A1B2 A2B2 A3B2
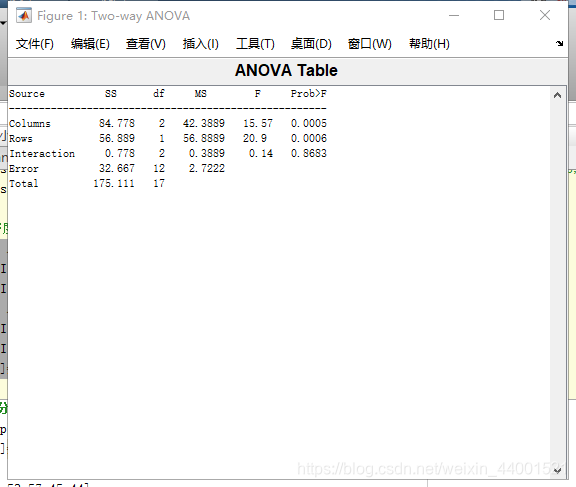
[p,table,stats]=anova2(X,3)

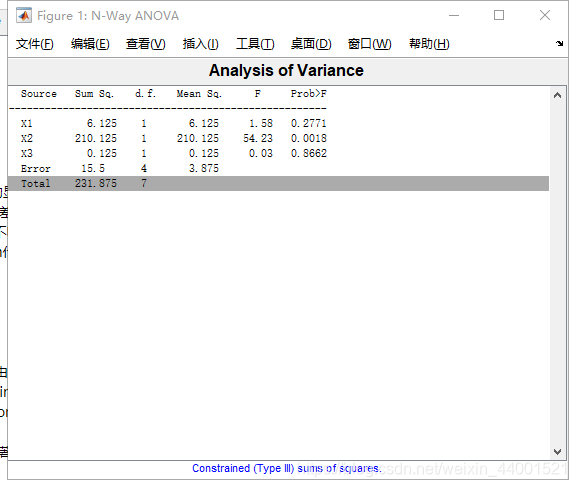
③多因素一元方差分析的方法和案例：
%案例
y=[52 57 45 44 53 57 45 44];
g1=[1 2 1 2 1 2 1 2];
g2={‘hi’;‘hi’;‘lo’;‘lo’;‘hi’;‘hi’;‘lo’;‘lo’};
g3={‘may’;‘may’;‘may’;‘may’;‘june’;‘june’;‘june’;‘june’};
[p,table,stats]=anovan(y,{g1,g2,g3})