文章采用均值为SMA(close, time_period = 3日),利用(收盘价 - 三日均线)计算偏离程度。
如果大于阈值(首个收盘价的2%)则开仓买入(卖出)
如果收盘价穿过均线说明均值偏离情况消失平仓。
文章采用Tick高频数据、也可以切换日收盘价数据进行改写。
话不多说上代码:
导出必要包和数据
import pandas as pd
import numpy as np
import datetime
import talib as tl
import warnings
from pyecharts import options as opts
from pyecharts.globals import ThemeType
from pyecharts.charts import Kline,Line, Bar, Grid,Scatterwarnings.filterwarnings("ignore")data = pd.read_csv('你的数据路径')使用Ta-Lib库计算SMA均线(本文采用Tick数据,如果换成日数据请注意修改参数)
查看一下偏离度与阈值的变化情况
data = x
data['month'] = data.index.map(lambda x: x.strftime('%Y.%m'))
data['time'] = data.index.map(lambda x: x.time())# 选取 阈值
threshold = data.close[0]*0.02
data['SMA'] = tl.SMA(data.close, len(data[(data.index.date==data.index.date[0])])*3)
data['distance'] = data['close'] - data['SMA']
data['threshold'] = thresholddf = data[['threshold', 'distance']].resample('1D').last().round(2)
df = df.dropna()
L_ = (Line(init_opts=opts.InitOpts(theme=ThemeType.MACARONS, width='900px', height='500px')).add_xaxis(df.index.tolist()).add_yaxis("距离",df['distance'].tolist()).add_yaxis("下轨",(df['threshold']*-1).tolist()).add_yaxis("上轨",df['threshold'].tolist()).set_global_opts(yaxis_opts=opts.AxisOpts(is_scale=True),xaxis_opts=opts.AxisOpts(is_scale=True),title_opts=opts.TitleOpts(title="收盘价到均值的距离&阈值情况"),datazoom_opts=[opts.DataZoomOpts(type_='inside')]))L_.render_notebook()
目测来看交易次数不多
遍历所有单元格查看买卖情况,文章使用tick级数据,预设实时计算均值、查看举止和收盘价之间的偏离度,一旦出现开仓信号则以买一(卖一)价格报单,在下一个3秒内成交。此处为了简化暂时没有考虑报单成交的情况,假设以下一个tick的收盘价成交。(如果使用日级别数据、可以将s_init, s 删除)
# 记录当前位置
position = 1# 记录当日可出售股票持仓
s_init = 5
# 记录整体股票持仓
s = s_init# 记录买单卖单
buy = []
sell = []
for i in range(0, len(data)-2):# 开仓判断# 偏离距离大于阈值,卖出if ((data['distance'][i] > threshold) & (data['distance'][i-1] < threshold) & (position==1) & (s_init>0)):sell.append([data.index[i+1], data['close'][i+1],200])position -= 1s_init -= 1s -= 1# 向下偏离且偏离距离大于阈值,买入elif ((data['distance'][i] < (-threshold)) & (data['distance'][i-1] > (-threshold)) & (position==1)):buy.append([data.index[i+1], data['close'][i+1],200])position += 1s += 1# 止盈平仓判断# 收盘价下穿均值,买入平仓elif ((position == 2) & (data['distance'][i]<= 0) & (data['distance'][i-1]>0) & (s_init>0)):sell.append([data.index[i+1], data['close'][i+1],200])position -= 1s_init -= 1s -= 1# 收盘价上穿均值,买入平仓elif ((position == 0) & (data['distance'][i]>= 0) & (data['distance'][i-1]<0)):buy.append([data.index[i+1], data['close'][i+1],200])position += 1s += 1if data.index[i].time() == datetime.time(15, 0):s_init = s# 最后收盘时平仓
if len(sell)< len(buy):sell.append([data.index[-1],data['close'][-1], 200])
elif len(sell)> len(buy):buy.append([data.index[-1],data['close'][-1], 200])
数据处理及盈亏计算
sell = pd.DataFrame(sell, columns = ['卖出时间', '卖出价格', '卖出数量'])
buy = pd.DataFrame(buy, columns = ['买入时间', '买入价格', '买入数量'])
sell.index = sell['卖出时间']
buy.index = buy['买入时间']
data = data.join(sell[['卖出价格','卖出数量']])
data = data.join(buy[['买入价格', '买入数量']])
data = data.round(2)
net_profit = (sell['卖出价格']*sell['卖出数量']*0.998).sum()-(buy['买入价格']*buy['买入数量']).sum()画图查看部分买入卖出情况,确保策略代码正常
data_plot = data[(data.month == data.month.unique()[3])]L_ = (Line(init_opts=opts.InitOpts(theme=ThemeType.MACARONS, width='900px', height='500px')).add_xaxis(data_plot.index.tolist()).add_yaxis("收盘价",data_plot['close'].tolist()).add_yaxis("均线上轨",(data_plot['SMA']+data_plot.threshold).round(2).tolist()).add_yaxis("均线",data_plot['SMA'].tolist()).add_yaxis("均线下轨",(data_plot['SMA']-data_plot.threshold).round(2).tolist()).set_global_opts(yaxis_opts=opts.AxisOpts(is_scale=True),xaxis_opts=opts.AxisOpts(is_scale=True),title_opts=opts.TitleOpts(title="均线&收盘价情况"),datazoom_opts=[opts.DataZoomOpts(type_='inside')]))S_ = (Scatter().add_xaxis(data_plot.index.tolist()).add_yaxis("卖出",data_plot['卖出价格'].tolist()).add_yaxis("买入",data_plot['买入价格'].tolist()).set_global_opts(yaxis_opts=opts.AxisOpts(is_scale=True),xaxis_opts=opts.AxisOpts(is_scale=True),datazoom_opts=[opts.DataZoomOpts(type_='inside')]))
L_.overlap(S_)
L_.render_notebook()
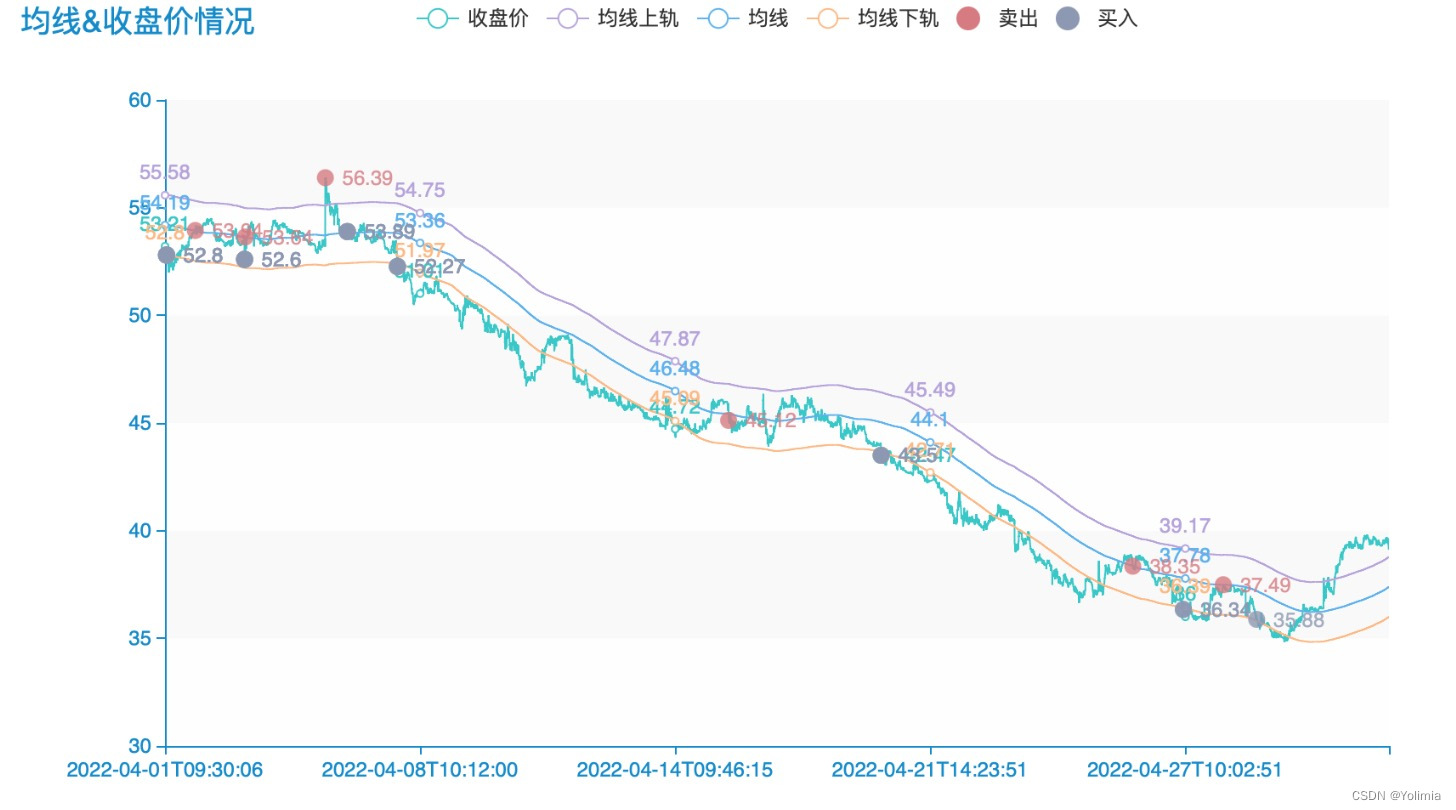
抽取的部分数据看出:不考虑配对情况的话,大部分买点是在买点上方。
画图查看股价变动和净盈亏之间的波动关系
data = data.fillna(0)
data['敞口'] = (data['买入数量'].cumsum()-data['卖出数量'].cumsum())
data['实现盈利'] = (data['卖出数量']*data['卖出价格']).cumsum()*0.998-(data['买入数量']*data['买入价格']).cumsum()
data['净盈亏'] = (data['敞口'])*data['close']+(data['实现盈利'])
data['净盈亏'] = data['净盈亏'].round(2)df = data[['close','净盈亏']].resample('1D').last()
df = df.dropna()L_ = (Line(init_opts=opts.InitOpts(theme=ThemeType.MACARONS, width='900px', height='500px')).add_xaxis(df.index.tolist()).add_yaxis("收盘价",df['close'].tolist(),yaxis_index=1).add_yaxis("盈亏",df['净盈亏'].tolist()).extend_axis(yaxis=opts.AxisOpts(axislabel_opts=opts.LabelOpts(formatter="{value}元"))) # 添加一条蓝色的y轴.set_global_opts(yaxis_opts=opts.AxisOpts(is_scale=True),xaxis_opts=opts.AxisOpts(is_scale=True),title_opts=opts.TitleOpts(title="均值回归交易策略--盈亏、股价变化情况)"),datazoom_opts=[opts.DataZoomOpts(type_='inside')]))L_.render_notebook()

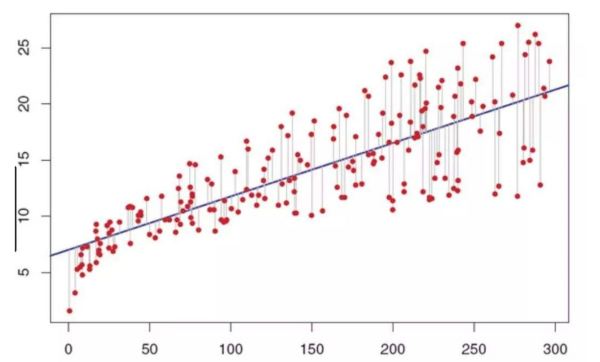
均值回归策略在震荡市表现优异,单边行情时表现较差,文章选取标的震荡行情较多,获得正向盈利且跑赢单纯持有。



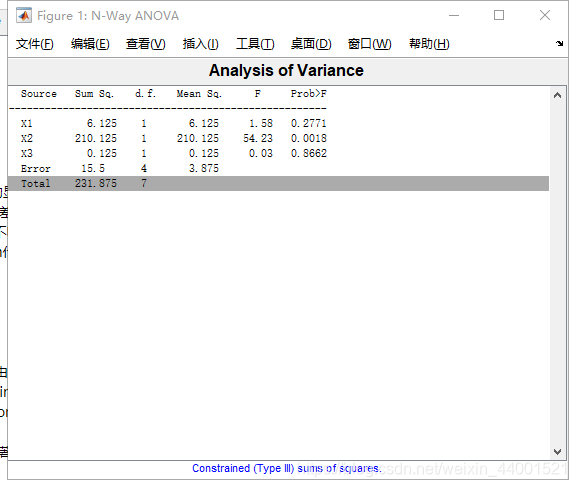
![[转] R 逐步回归分析 AIC信息统计量](https://images0.cnblogs.com/i/388224/201405/122323393753359.jpg)