题目描述:
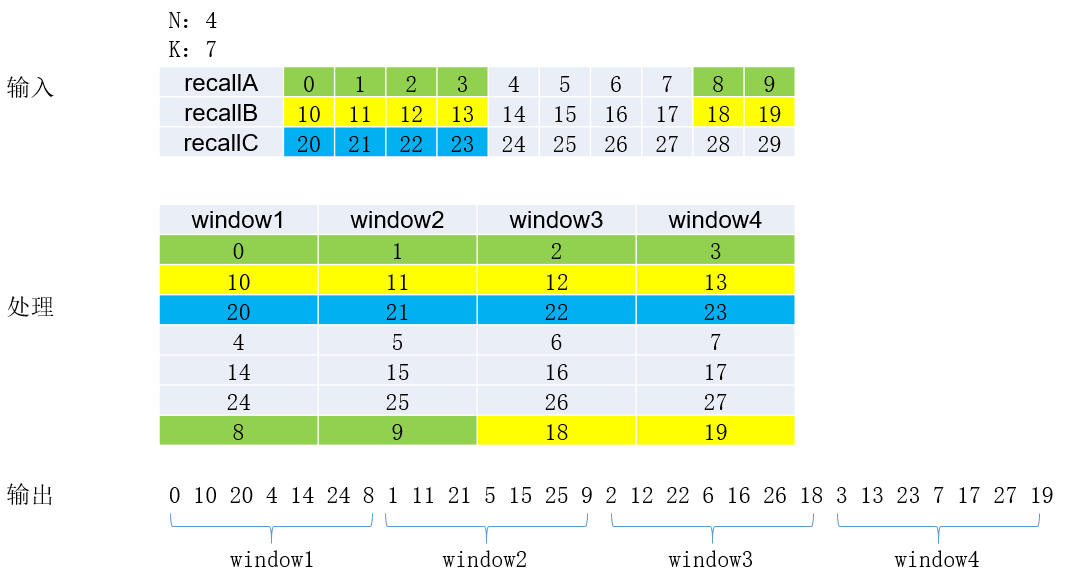
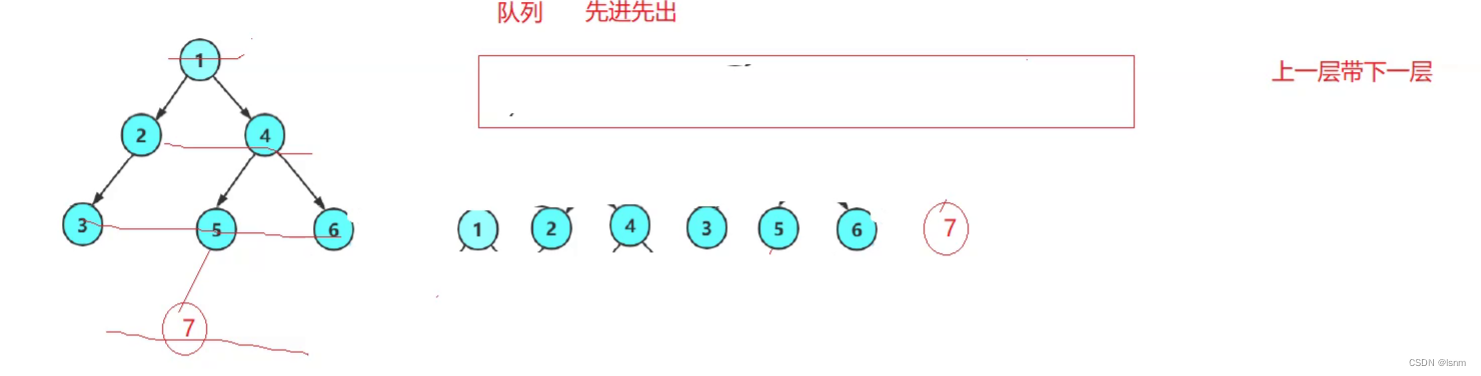
推荐多样性需要从多个列表中选择元素,一次性要返回N屏数据(窗口数量),每屏展示K个元素(窗口大小),选择策略:
1. 各个列表元素需要做穿插处理,即先从第一个列表中为每屏选择一个元素,再从第二个列表中为每屏选择一个元素,依次类推
2. 每个列表的元素尽量均分为N份,如果不够N个,也要全部分配完,参考样例图:
(1)从第一个列表中选择4条0 1 2 3,分别放到4个窗口中
(2)从第二个列表中选择4条10 11 12 13,分别放到4个窗口中
(3)从第三个列表中选择4条20 21 22 23,分别放到4个窗口中
(4)再从第一个列表中选择4条4 5 6 7,分别放到4个窗口中
...
(5)再从第一个列表中选择,由于数量不足4条,取剩下的2条,放到窗口1和窗口2
(6)再从第二个列表中选择,由于数量不足4条并且总的元素数达到窗口要求,取18 19放到窗口3和窗口4
输入描述:
第一
华为OD机试真题-推荐多样性-2024年OD统一考试(C卷)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/287725.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
2016年认证杯SPSSPRO杯数学建模D题(第一阶段)NBA是否有必要设立四分线解题全过程文档及程序
2016年认证杯SPSSPRO杯数学建模
D题 NBA是否有必要设立四分线
原题再现 NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力挽狂澜的&am…
lvgl 窗口 windows lv_port_win_visual_studio 版本 已解决
不知道的东西,不知道lvgl窗口。一切从未知开始 lv_port_win_visual_studio 主分支 对应的分支 v7版本更新git submodule update --init --recursive同步 lvgl代码随后打开 visualSudio 打开.sln 文件 编译 release模式 允许 一切正常代码部分
建筑结构设计的内容与要求,建筑工程结构设计资料大全
一、资料描述
本套建筑设计资料,大小4.62G,1个压缩文件。
二、资料目录
0-结构设计
1-快速建模方法
A-satwe资料
B-剪力墙资料
C-地下室资料
D-基础
E-楼梯
F-水池
G-砖混结构
H-挡土墙
I-框剪结构
J-常用规范
K-配筋率计算方法
L-底框结…
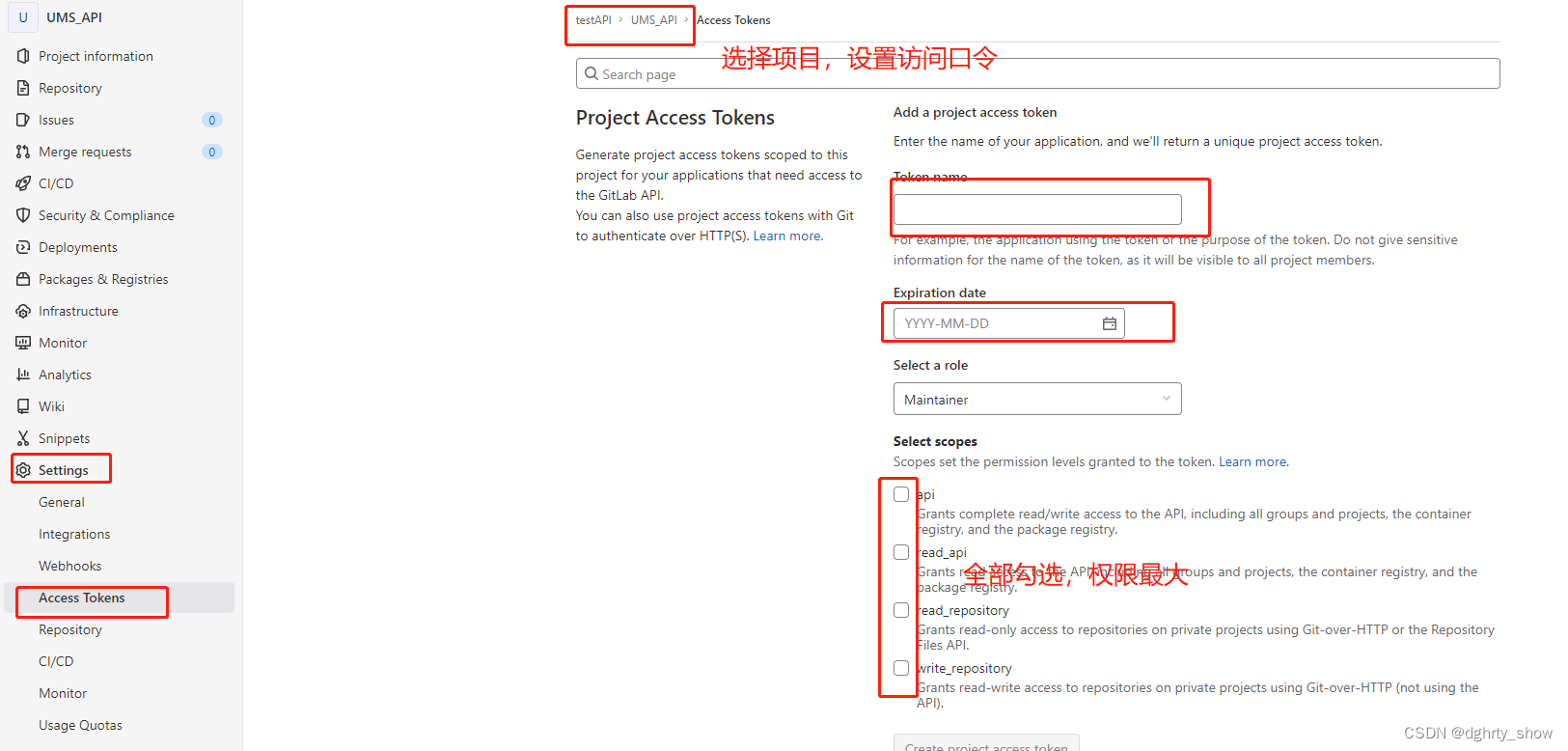
jenkins配置源码管理的git地址时,怎么使用不了 credential凭证信息
前提
Jenkins使用docker部署
问题
(在jenlins中设置凭证的方式)在Jenkins的任务重配置Git地址,并且设置了git凭证,但是验证不通过,报错; 无法连接仓库:Command "git ls-remote -h -- http://192.1XX.0.98:X02/…
C语言 青蛙跳台阶问题
目录 编辑
1.问题描述
2.问题分析
3.全部代码
4.结语 1.问题描述
一只青蛙可以一次跳一级台阶,也可以一次跳两级台阶,如果青蛙要跳上n级台阶有多少种跳法?
2.问题分析
当台阶只有一级时,只能跳一级,所以只有一…
C语言数据结构基础————二叉树学习笔记(四)简单的OJ题目练习
1.单值二叉树
965. 单值二叉树 - 力扣(LeetCode)
建立一个新的函数,用函数传参的方法来记录val的值
如上一篇最后的对称二叉树的习题,建立新的函数来传参 多采用使用反对值的方法,因为如果是相等return true的话&am…
Spring框架介绍及详细使用
前言
本篇文章将会对spring框架做出一个比较详细的讲解,并且每个知识点基本都会有例子演示,详细记录下了我在学习Spring时所了解到全部知识点。 在了解是什么spring之前,我们要先知道spring框架在开发时,服务器端采用三层架构的方…
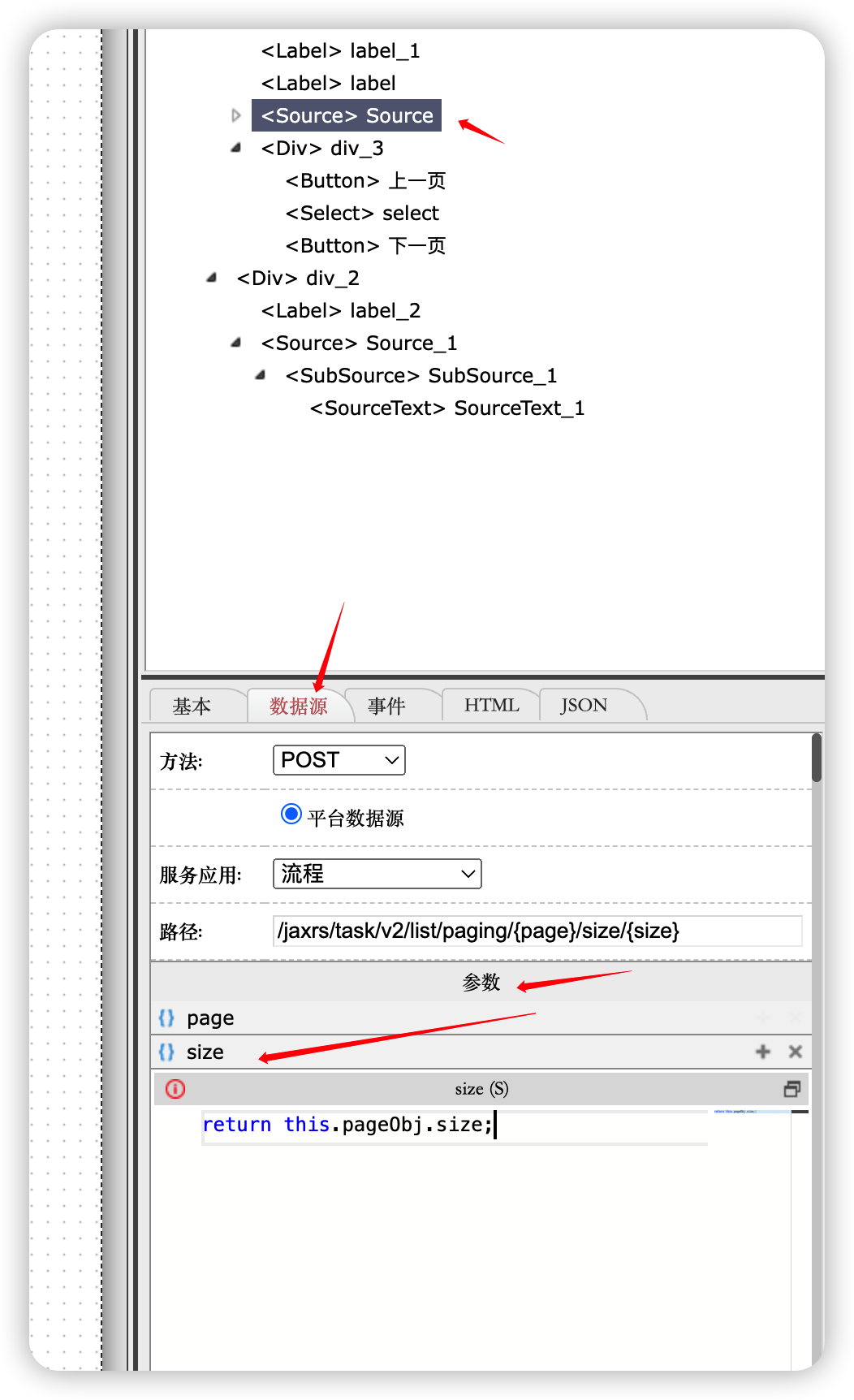
O2OA(翱途)开发平台-快速入门开发一个门户实例
O2OA(翱途)开发平台[下称O2OA开发平台或者O2OA]拥有门户页面定制与集成的能力,平台通过门户定制,可以根据企业的文化,业务需要设计符合企业需要的统一信息门户,系统首页等UI界面。本篇主要介绍通过门户管理系统如何快速的进行一个…
大数据面试题 —— Kafka
目录 消息队列 / Kafka 的好处消息队列的两种模式什么是 KafkaKafka 优缺点你在哪些场景下会选择 Kafka讲下 Kafka 的整体结构Kafka 工作原理 / 流程Kafka为什么那么快/高效读写的原因 / 实现高吞吐的原理生产者如何提高吞吐量(调优)kafka 消息数据积压&…
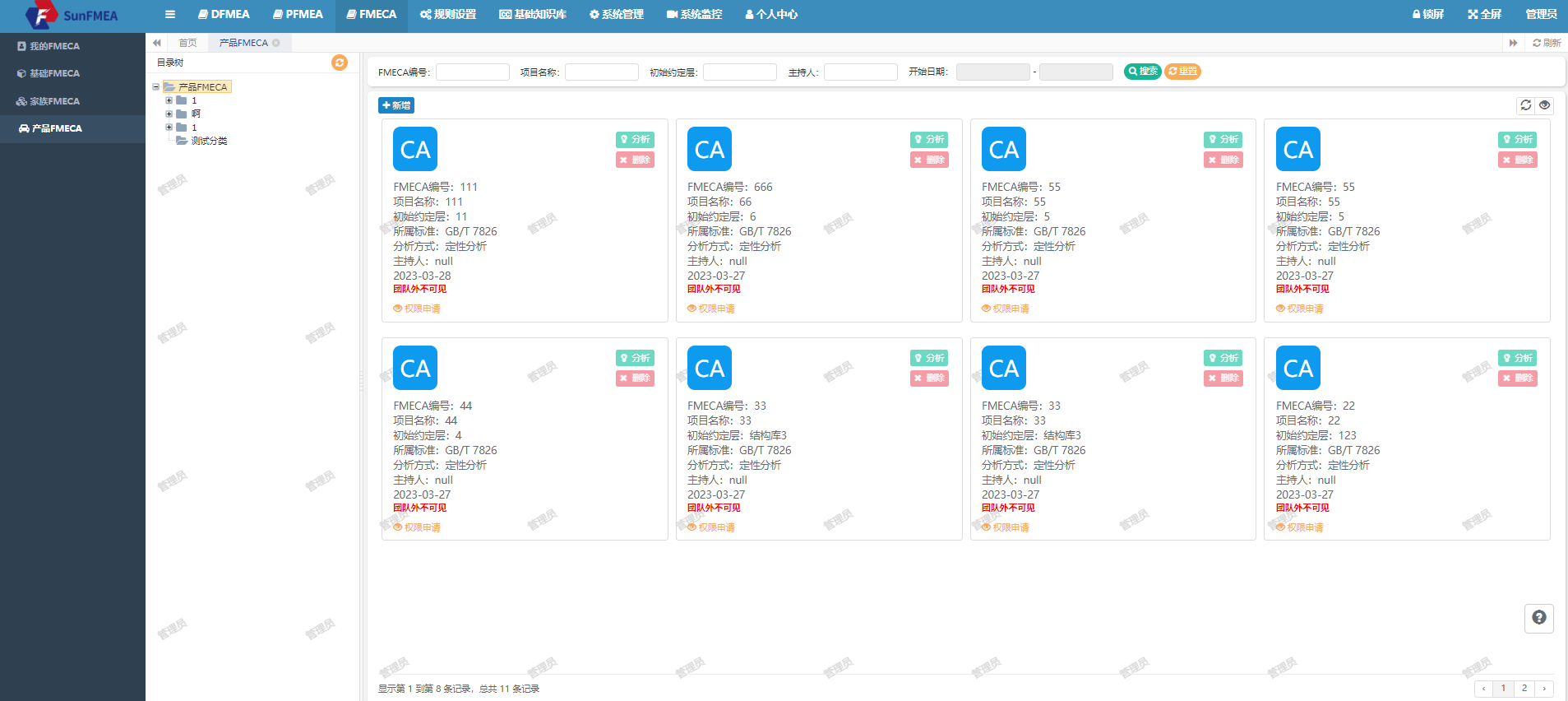
在FMEA风险控制中,首检的重要性!——SunFMEA软件
在制造业中,FMEA被广泛应用于产品设计、生产过程和产品服务的各个阶段。而首检,作为生产过程中的一个重要环节,同样承载着风险控制和质量保障的重任。 今天SunFMEA软件系统从FMEA风险控制的角度来看,首检具有至关重要的地位。首检…
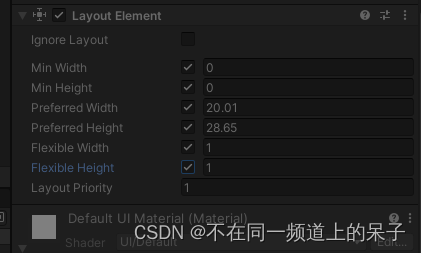
Unity 布局元素Layout Element
Layout Element是一种用于控制UI元素在布局组件(如Horizontal Layout Group、Vertical Layout Group、Grid Layout Group、Content Size Fitter和Aspect Ratio Fitter)中的大小和位置的组件。Layout Element组件可以附加到UI元素上,以便在布局…
How to convert .py to .ipynb in Ubuntu 22.04
How to convert .py to .ipynb in Ubuntu 22.04 jupyter nbconvertp2j 最近看到大家在用jupyter notebook,我也试了一下,感觉还不错,不过,也遇到了一些问题,比方说,我有堆的.py文件,如果要一个一…
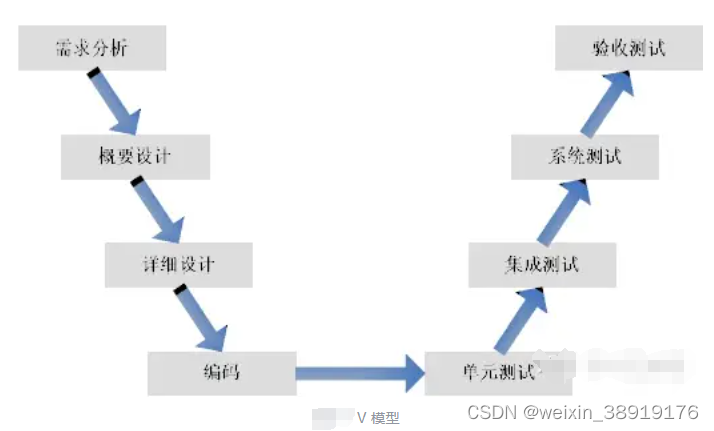
软件测试-生命周期、模型
软件测试知识梳理 软件测试软件测试生命周期软件测试模型 软件测试
通过对软件系统进行测试,发现并修复其中潜在的缺陷,确保软件的质量和稳定性。
软件测试生命周期
指软件测试在整个软件开发过程中的各个阶段。
需求分析 在测试周期的初期阶段&…
基于XGBoost和数据预处理的电动汽车车型预测
基于XGBoost和数据预处理的电动汽车车型预测 文章目录 基于XGBoost和数据预处理的电动汽车车型预测1、前言2、导入数据3、各县电动汽车采用情况条形图4、电动车类型饼图5、前5最欢迎的电动车制造商6、XGBoost模型6.1 字符串列的标识6.2 删除不相关的列6.3 编码分类变量6.4 电动…
Python 全栈体系【四阶】(二十)
第五章 深度学习
二、推荐系统
1. 推荐算法介绍
1.1 个性化推荐算法 人口属性 地理属性 资产属性 兴趣属性
1.2 推荐算法分支
协同过滤推荐算法基于内容的推荐算法混合推荐算法流行度推荐算法
1.3 推荐算法
为推荐系统选择正确的推荐算法是非常重要的决定。目前为止…
【机器学习之---数学】统计学基础概念
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog
0. 前言
统计学基础
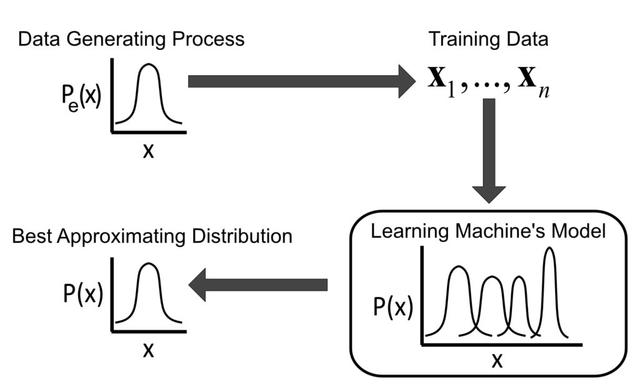
1. 频率派
频率学派(传统学派)认为样本信息来自总体,通过对样本信息的研究可以合理地推断和估计总体信息…
6、ChatGLM3-6B 部署实践
一、ChatGLM3-6B介绍与快速入门 ChatGLM3 是智谱AI和清华大学 KEG 实验室在2023年10月27日联合发布的新一代对话预训练模型。ChatGLM3-6B 是 ChatGLM3 系列中的开源模型,免费下载,免费的商业化使用。 该模型在保留了前两代模型对话流畅、部署门槛低等众多…