Denoising Diffusion Probabilistic Models

这篇文章就是所谓的DDPM

前向扩散过程之和前一步有关，是一阶马尔可夫链，是图像和标准高斯噪声I的加权，认为方差全部来自I，并且多步可以通过连乘合并为一步：

反向的过程也是类似的形式：

并且由贝叶斯公式，并且贝叶斯中三个概率都是高斯分布，可以得到：

GaussianDiffusionTrainer

首先明确扩散时的一步转移公式。表现形式为信号以某一系数进行衰减，同时加一个高斯噪声（高斯噪声为加性信号无关的高斯噪声）。

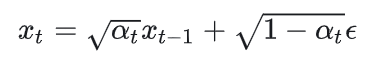
因为本质就是信号与高斯噪声的alpha blending，所以就需要考虑权重的选择。特别的是前一个状态的信号 $x_{t-1}$ 和噪声的权重之和不是1，而是他们两个平方和才是1。因为这里关心的不是像素值，而是方差，而方差的变化与系数是平方关系。

对不同时刻的转移，权重系数是不同的，但是所使用的高斯噪声是固定的。再加上alpha blending本质是线性操作，所以多步转移可以合并为一个：

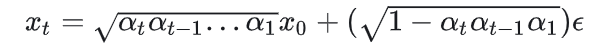
简写为：

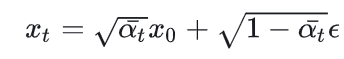
扩散过程可以压缩为一步，每步的衰减系数连乘。可以看到代码中的beta表示的是噪声部分的权重，是等差递增的。利用这个等差数组计算连乘，得到每个时刻的权重：

class GaussianDiffusionTrainer(nn.Module): def __init__(self, model, beta_1, beta_T, T): super().__init__() self.model = model self.T = T self.register_buffer( 'betas', torch.linspace(beta_1, beta_T, T).double()) #beta_T取0.02，T取1000,噪声的去噪betas是递增等差数列 alphas = 1. - self.betas #意味着\alpha_t是递减的，这是信号的权重，加上噪声的权重方差和是1                 alphas_bar = torch.cumprod(alphas, dim=0) #计算累乘，得到\sqrt(\hat(\alpha_t))，从0直接到t的累积权重 
# calculations for diffusion q(x_t | x_{t-1}) and others 
self.register_buffer( 'sqrt_alphas_bar', torch.sqrt(alphas_bar)) self.register_buffer( 'sqrt_one_minus_alphas_bar', torch.sqrt(1. - alphas_bar)) # 得到原始信号和噪声的权重，并且注册到内存中 
def forward(self, x_0): 
""" Algorithm 1. """ t = torch.randint(self.T, size=(x_0.shape[0], ), device=x_0.device) # t的区间是    [0,T),x_0.shape[0]指的就是batchsize noise = torch.randn_like(x_0) # x_0是原始信号，所以噪声也要是相同尺寸的高斯分布 x_t = ( extract(self.sqrt_alphas_bar, t, x_0.shape) * x_0 +     extract(self.sqrt_one_minus_alphas_bar, t, x_0.shape) * noise) #时刻t的信号 loss = F.mse_loss(self.model(x_t, t), noise, reduction='none') 计算模型的预测与使用的高斯噪声的mse loss return loss

beta的范围是[0.0001,0.02]，意味着信号部分的权重alpha是[0.9999,0.98]。虽然信号部分权重很接近于1，但你要知道指数的力量：

np.power(0.99,1000)=4.3e-5。这意味着beta的取值会使得1000步之后几乎完全是一个高斯噪声。事实上，1000步之后高斯噪声的权重已经达到0.9999.

解释一下forward函数的含义。 $x_0$ 表示一个batch的图像送入，forward的时候会先随机生成长度为batch的t，表示这批batch图的不同样本会经历不同时长的扩散，这些时长是在(0,1000)中随机取的，这样就可以模拟不同程度的扩散。因为使用向量运算，可以同时得到一个batch中所有图的扩散结果x_t.

除了扩散步长是随机的，扩散中所使用的噪声在不同batch之间也是随机的。这意味着我们模拟了同一幅图在不同噪声水平下，不同扩散步长下的扩散结果。

loss的计算。GaussianDiffusionTrainer还有一个成员函数model。model通常是一个unet，它的输入是x_t和t，是为了估计扩散时所使用的noise。所以计算loss是在model的输出和扩散过程所使用的噪声之间计算mse，因为网络就是来估计这个噪声的，这个噪声直接决定了反向过程的计算，详细原因可以看下面小节。

GaussianDiffusionSampler

后验概率也是高斯分布

后向转移其实就是求后验概率，所以可以使用贝叶斯公式：

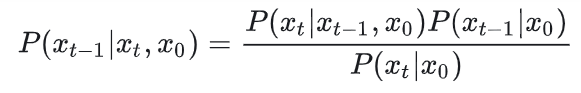
上式中每一项概率都可以用x_0及扩散时的系数表示出来，并且每一项都是高斯分布：

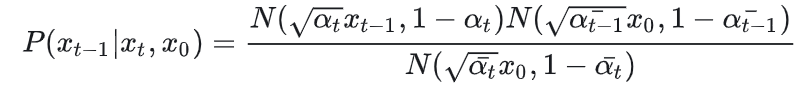
贝叶斯公式中的概率都是高斯分布，所以可以认为 $P(x_{t-1}|x_t,x_0)$ 也是高斯分布

前一步均值是首尾的加权和

既然是高斯分布，把上面式子化简为高斯分布的格式，其实就是得到 $x_{t-1}$ 均值和方差：

这是求前一步均值和方差的相关代码，其中均值的表达式是初始时刻和扩散结果 $x_0,x_t$ 的加权和，所以需要先计算两个权重系数：

    self.register_buffer('betas', torch.linspace(beta_1, beta_T, T).double())alphas = 1. - self.betasalphas_bar = torch.cumprod(alphas, dim=0) # t时刻的累计乘alphas_bar_prev = F.pad(alphas_bar, [1, 0], value=1)[:T]  #前面补1，相对于整体右移了，得到t-1时刻的累计乘# variance for posterior q(x_{t-1} | x_t, x_0)self.register_buffer('posterior_var',self.betas * (1. - alphas_bar_prev) / (1. - alphas_bar))# below: log calculation clipped because the posterior variance is 0 at# the beginning of the diffusion chainself.register_buffer('posterior_log_var_clipped',torch.log(torch.cat([self.posterior_var[1:2], self.posterior_var[1:]])))
# 因为后验的方差涉及到alpha_bar_prev，做法是把alpha_bar右移一位，前面补0。
# 这样的话的方差就会是0，所以把所求出的方差构成的list的第一个元素使用第二个取代# mean for posterior q(x_{t-1} | x_t, x_0)self.register_buffer('posterior_mean_coef1',torch.sqrt(alphas_bar_prev) * self.betas / (1. - alphas_bar))  # x_0的系数self.register_buffer('posterior_mean_coef2',torch.sqrt(alphas) * (1. - alphas_bar_prev) / (1. - alphas_bar))  # x_t的系数

可以看到上面求均值和方差时基本上都是和衰减系数相关的。比如连乘alphas_bar 和alphas_bar_prev，当然还有t时刻的信号权重alpha_t.

齿轮转动需要x_0

注意到上式在求均值时需要用到x_0，而x_0其实是我们最终要复原的。这无异于鸡生蛋蛋生鸡的问题。

其中一个解决办法是先随机选取一个点，然后不停地去迭代更新。比如牛顿迭代法，EM算法，K-means算法都是这个思想。不过当然初始值越准确越好，这里可以先将x_0表示为：

进一步简化： $x_0=\sqrt(\frac{1}{\bar\alpha_t} )x_t-\sqrt(\frac{1}{\bar\alpha_t}-1) \varepsilon$

发现 $x_0$ 又是扩散终点状态 $x_t$ 和噪声 $\varepsilon$ 的加权和。从而有下面的代码，计算权重来估计x_0:

# calculations for diffusion q(x_t | x_{t-1}) and others
# x_t和eps的系数分别是sqrt(1/alphas_bar)和sqrt(1. / alphas_bar - 1))self.register_buffer('sqrt_recip_alphas_bar', torch.sqrt(1. / alphas_bar))
self.register_buffer('sqrt_recipm1_alphas_bar', torch.sqrt(1. / alphas_bar - 1))def predict_xstart_from_eps(self, x_t, t, eps):assert x_t.shape == eps.shapereturn (extract(self.sqrt_recip_alphas_bar, t, x_t.shape) * x_t -extract(self.sqrt_recipm1_alphas_bar, t, x_t.shape) * eps)

需要的其实是eps

把x_0的计算公式再代入上面的后向一步转移概率，得到从下面的式子。可以看出，后向转移概率的均值和方差都要知道扩散时的权重，而均值还需要知道diffusion过程中使用的高斯噪声eps。扩散时的权重是提前设定的，所以是已知的， $x_t$ 也是已知的，所以现在的关键就是求取噪声eps。

对于不同batch图像的diffusion，转移的权重是固定的list（可以认为是只和时间相关的），而高斯噪声eps是每次随机得到的。从这个角度说，噪声和图像又有某些抽象的联系，如何从寻找一个最优的标准高斯噪声，我们可以使用unet来学习得到eps。

恢复上一步信号

结合上面两个分别求x_0和求权重的代码块，可以得到：

def q_mean_variance(self, x_0, x_t, t):"""Compute the mean and variance of the diffusion posteriorq(x_{t-1} | x_t, x_0)"""assert x_0.shape == x_t.shapeposterior_mean = (extract(self.posterior_mean_coef1, t, x_t.shape) * x_0 +extract(self.posterior_mean_coef2, t, x_t.shape) * x_t)posterior_log_var_clipped = extract(self.posterior_log_var_clipped, t, x_t.shape)return posterior_mean, posterior_log_var_clipped

得到均值和方差之后，知道了均值和方差，就可以构建上一时刻的信号。一步步迭代，就可以起到恢复图像的效果：

def forward(self, x_T):"""Algorithm 2."""x_t = x_Tfor time_step in reversed(range(self.T)): # 注意这里的reversedt = x_t.new_ones([x_T.shape[0], ], dtype=torch.long) * time_step  # 得到一个batch的time_stepmean, log_var = self.p_mean_variance(x_t=x_t, t=t)# no noise when t == 0if time_step > 0:noise = torch.randn_like(x_t) # 引入(0,1)的高斯噪声else:noise = 0x_t = mean + torch.exp(0.5 * log_var) * noise  # 噪声的权重为var的开根号x_0 = x_treturn torch.clip(x_0, -1, 1)

注意均值其实就是恢复出的信号，再按照估计的方差大小，叠加对应的随机高斯噪声。这样做的好处是保持了生成的可能性和多样性。

估计完上一步之后，还要估计上上一步，仍然需要计算均值和方差，而这就要网络估计eps。这也就是为什么训练阶段就需要扩散到不同程度的原因，这样网络才可以从不同扩散时刻的信号中估计出噪声eps。

实验

0	10000	14000	18000	74000

疑问：

变分推理，求x_0需要先知道x_0，取代积分？和熵+KL优化的区别？
前向后向都是高斯的依据
训练求eps，也可以训练求x_t-1?
后验概率方差求cat和log？cat的原因是代码中的注释所写的，求log是为了避免溢出？
eps可以认为是退化核？unet的作用是寻找最优的？最符合这个图的核？
渐进的有损解压progressive lossy decompression

自回归解码的泛化generalization of autoregressive decoding
和传统去噪算法对比：

f(原始信号,noise) GT：干净图像，估计的噪声和图像内容强相关。

f(原始信号, t ,noise) GT：高斯噪声。

残差的时候都可以看作是学习噪声分布。

区别： 1. diffusion还有时间t的影响。

2.diffusion的噪声分布是高斯的，信号无关的。

3.去噪的时候可以直接拿到带噪声的信号，生成的时候输入是标准高斯，加入文本模型的指导也是高斯？但是扩散的时候1000步之后不一定是高斯吧

4.去噪可以直接由残差得到干净图，生成因为是多步的，只能根据高斯噪声一步步转移回去。5.扩散的阶段是使用同一个高斯噪声，采样的阶段不是同一个。