一、链表概述

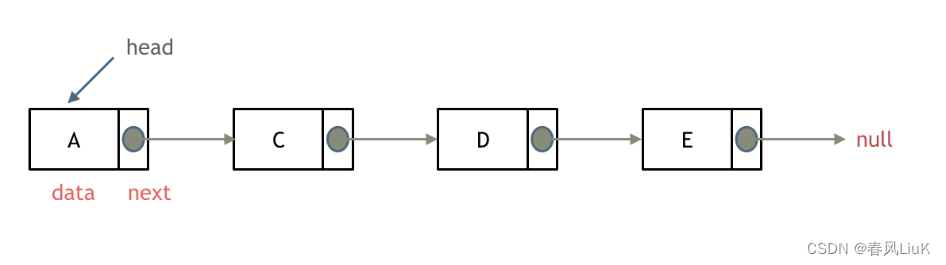
1.1概述

在C++中，链表是一种线性数据结构，但它并不像数组那样在内存中存储连续的元素，而是通过每个元素（通常称为节点）包含一个指向下一个节点的指针来链接各个元素。链表的节点通常包含两部分：数据域（存储元素值）和指针域（存储指向下一个节点的指针）。

1.2链表的组成部分：

1. 节点（Node）：
   一个节点通常定义为一个结构体或类，包含数据和指向下一个节点的指针（在单链表中），或者前后节点指针（在双向链表中）。

   // 单链表节点示例
   struct ListNode {int value; // 数据域ListNode* next; // 指针域，指向下一个节点
   };
   

2. 链表操作：

   • 创建链表：链表通常从一个空节点（即头节点）开始，头节点的 next 指针可能指向实际数据的第一个节点，也可能为空（表示链表为空）。
   • 插入节点：在链表的任意位置插入一个新节点，涉及更改相应节点的指针以建立新的链接关系。
   • 删除节点：从链表中移除一个节点，需要更新其前驱节点的指针跳过被删除节点。
   • 遍历链表：通过从头节点开始，沿着 next 指针逐个访问节点，直至遇到 next 为 nullptr 的节点（链表尾部）。
   • 查找节点：通过遍历链表查找具有特定值的节点。

1.3链表的优缺点：

• 优点：
  • 动态扩展：无需预先知道数据规模，可以根据需要动态添加或删除节点。
  • 插入和删除效率较高：在链表头部或尾部插入和删除的时间复杂度一般为O(1)，在中间插入和删除的时间复杂度为O(n)（需要找到插入或删除位置）。
• 缺点：
  • 访问效率相对较低：随机访问一个节点的时间复杂度为O(n)，因为需要从头节点开始顺着指针找到目标节点。
  • 需要额外存储指针的空间开销。

在实际编程中，链表还会有多种变形，比如双向链表、循环链表、带头节点的链表等，每种都有其特定的应用场景和操作特点。

二、链表典例

力扣707.设计链表

原题链接

难点分析：

/*** Your MyLinkedList object will be instantiated and called as such:* MyLinkedList* obj = new MyLinkedList();* int param_1 = obj->get(index);* obj->addAtHead(val);* obj->addAtTail(val);* obj->addAtIndex(index,val);* obj->deleteAtIndex(index);*/

（1）MyLinkedList成员变量的确定：

由题目中透露出的信息：

• int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1
• void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将 不会插入 到链表中。

我们可以知道，我们最好进行链表长度的维护，这样在验证index的合法性时，不需要每一次都遍历整个链表，直接调用我们维护的长度即可：

    //选择单链表作为此类的底层实现，定义单链表结构体struct ListNode{int val; //值ListNode* next; //链，指向下一个节点的内存地址ListNode(int val):val(val), next(nullptr){}};//虚拟头节点，简化代码，后面详细介绍ListNode* _dummyNode;//维护链表长度int _size;

（2）初始化自定义链表：

力扣在进行代码测试时，会将MyLinkedList初始化为一个对象，后续所有函数调用都是通过这个对象进行的，因此我们需要对这个对象进行初始化，即编写构造函数。

    //类的构造函数，初始化自定义链表对象MyLinkedList() {//初始化虚拟头节点，统一节点的删除操作_dummyNode = new ListNode(0); //调用底层链表有参构造函数初始化_size = 0; //虚拟头节点不计入长度计算}

（3）底层链表的选择：

MyLinkedList这个类需要基于单链表或双向链表实现，不同的选择会写出不同的代码，我为了优化代码，选择了带虚拟头结点的链表（单链表）作为底层数据结构。

    //定义单链表结构体struct ListNode{int val; //值ListNode* next; //链，指向下一个节点的内存地址ListNode(int val):val(val), next(nullptr){}};

完整代码：

class MyLinkedList {
private://定义单链表结构体struct ListNode{int val; //值ListNode* next; //链，指向下一个节点的内存地址ListNode(int val):val(val), next(nullptr){}};ListNode* _dummyNode;int _size;public://类的构造函数，初始化自定义链表对象MyLinkedList() {//初始化虚拟头节点，统一节点的删除操作_dummyNode = new ListNode(0); //调用有参构造函数初始化_size = 0; //虚拟头节点不计入长度计算}int get(int index) {if(_size == 0 || index > _size - 1|| index < 0){return -1;}else{//链表是链式的，在内存中是随机分布的，并不是线性连续，因此不能随机访问，而是通过指针连接ListNode* cur = _dummyNode->next;while(index--){cur = cur->next;}return cur->val;}}void addAtHead(int val) {//申请内存，生成新节点ListNode* newNode = new ListNode(val);//插入头节点newNode->next = _dummyNode->next;_dummyNode->next = newNode;//维护链表长度_size++;}void addAtTail(int val) {//申请内存，生成新节点ListNode* newNode = new ListNode(val);//移动指针，找到最后一个链表节点int index = _size;ListNode* cur = _dummyNode;while(cur->next != nullptr){cur = cur->next;}cur->next = newNode;_size++;}void addAtIndex(int index, int val) {if(index > _size) return;if(index < 0) index = 0;//申请内存，生成新节点ListNode* newNode = new ListNode(val);//移动指针到达index下标对应节点的前一个位置//_dummyNode开始指向虚拟节点ListNode* cur = _dummyNode;while(index--){cur = cur->next;}newNode->next = cur->next;cur->next = newNode;_size++;}void deleteAtIndex(int index) {if (index >= _size || index < 0) {return;}ListNode* cur = _dummyNode;while(index--){cur = cur->next;}ListNode* temp = cur->next;cur->next= cur->next->next; delete temp;//避免野指针temp = nullptr;_size--;}
};/*** Your MyLinkedList object will be instantiated and called as such:* MyLinkedList* obj = new MyLinkedList();* int param_1 = obj->get(index);* obj->addAtHead(val);* obj->addAtTail(val);* obj->addAtIndex(index,val);* obj->deleteAtIndex(index);*/

力扣206.翻转链表

原题链接

难点分析：

（1）翻转方式的选择：

在提及翻转一个字符串或数组时，我们常常想到STL中的reverse()函数，如果题目中不允许我们使用，那么我们可以使用双指针，一个指针指向待翻转的序列的首元素，另一个指针指向序列的尾元素，向中间循环迭代，交换两个指针指向的元素：

void reverseString(vector<char>& s) {for (int i = 0, j = s.size() - 1; i < s.size()/2; i++, j--) {swap(s[i],s[j]);}
}

这种方式是基于数组可以随机存取的，由于有这个性质，用上述双指针方式实现序列翻转十分优美，但是链表并不能随机存取，我们每次寻找到前后两个要交换的元素需要维护很多额外的变量，因此链表不适合这种翻转方式。结合链表的性质，我们可以使用两种翻转策略：

• 原地翻转：考虑链表的指针域的特点，改变链表中所有节点的指针指向，即node1->node2变为node1<-node2
• 借助额外的空间：利用栈先后进先的特点，实现翻转

完整代码：

（1）借助栈翻转：

class Solution {
public:ListNode* reverseList(ListNode* head) {if(head == nullptr) return nullptr;// 利用栈的性质，将链表的节点逆序链接，形成一个新的链表std::stack<ListNode*> st;// 定义一个指针遍历链表,装栈ListNode* cur = head;while (cur != nullptr) {// 向栈中压入当前节点的地址st.push(cur);// 指针向后移动cur = cur->next;}// 翻转后的链表的头节点是栈顶元素ListNode* newHead = st.top();st.pop();ListNode* pre = newHead;while (!st.empty()) {// 取当前栈顶元素，栈顶元素是一个存储ListNode类型的地址，可以用指针变量暂存ListNode* newNode = st.top();// 上一个已经出栈节点的指针域指向当前的栈顶元素pre->next = newNode;// 更新栈顶元素的 next 指针为 nullptr，断开原链表的原始链接newNode->next = nullptr;st.pop();pre = newNode;}return newHead;}
};

(2)原地翻转：

class Solution {
public:ListNode* reverseList(ListNode* head) {if(head == nullptr) return nullptr;//定义一个指针，实现链表的遍历ListNode* cur = head;//定义一个指针，实现链表的翻转ListNode* pre = nullptr;//定义一个临时指针，用于存放下一个节点位置ListNode* temp;while(cur){//暂存当前节点的下一个节点temp = cur->next;//翻转cur->next = pre; //将cur指向（连接）上一个节点，也断开了cur当前指向的节点与原链表下一个节点之间的链接//迭代(移动cur和pre)pre = cur; //将pre移动到本次处理的位置cur = temp; //cur移动到本次处理的下一个位置}return pre;}
};

力扣92.翻转链表Ⅱ

原题链接
这道题力扣的官方题解很详尽了，我这里提供一种借助栈"空间换时间"的解法：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseBetween(ListNode* head, int left, int right) {//本题链表的下标从1开始，并且链表中至少有一个元素//本题提供的左右边界一定是合法的//如果只有一个节点，或者只翻转1个节点，不论如何翻转都是一样的，可以直接返回if(head->next == nullptr || left == right) return head;//难点：//1.如何确定开始翻转的位置//2.如何确定终止翻转的位置//3.如何正确处理边界问题：//边界情况：//（1）整个链表都需要翻转// (2)left是链表第一个节点// (2)right是链表最后一个节点//思路：引入栈，将需要翻转局部的节点压入栈中，"倒出"实现局部翻转stack<ListNode*> st;//引入虚拟头节点，处理左边界问题ListNode* dummyNode = new ListNode({0, head});ListNode* cur = dummyNode;int cnt = 0; //记录cur当前的位置while(cur->next != nullptr){//还没到开始翻转的左边界，继续向链表后面遍历//如果到了翻转局部的前一个节点，就要开始处理了if(cnt < left - 1){cur = cur->next;//每到达一个节点，计数器加一cnt++;continue;}else if(cnt <= right){//翻转范围之前的节点//记录，用于链表的整体串联ListNode* pre = cur;//从翻转范围的第一个元素开始入栈cur = cur->next;cnt++;//标志变量，right就是链表的最后一个元素bool flag = false;//只要在链表中的位置不超过right，都入栈while(cnt <= right){st.push(cur);//只有下一个节点不为空，才迭代指针curif(cur->next != nullptr){cur = cur->next;}else{//如果在cnt<=right的情况下，发生了下一个节点为空的情况，说明right位置就是链表的最后一个节点flag = true;}             cnt++;}//翻转范围内的元素全部入栈完毕，开始翻转while(!st.empty()){ListNode* temp = st.top();//链接pre->next = temp;//指针后移pre = temp;pre->next = nullptr; //断开原来的链接st.pop();}if(!flag)pre->next = cur;}else{break;}}return dummyNode->next;}
};

力扣.24两两交换链表中的节点

原题链接
这道题其实是力扣25.k个一组翻转一次的简化版，两两交换不就是两个一组翻转一次吗？
我在字节客户端一面是遇到了这道算法题。

难点分析:

（1）处理边界：

这道题引入头节点就可以很方便地处理边界问题，简单模拟就可以实现交换。

完整代码：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {//模拟交换，引入虚拟头节点简化边界处理ListNode* dummyNode = new ListNode(0);dummyNode->next = head;ListNode* cur = dummyNode;while(cur->next != nullptr && cur->next->next != nullptr){//以4个节点为1组，交换中间两个节点，1号和4号节点用于处理边界问题//保存1号节点的地址ListNode* temp1 = cur->next;//保存4号节点的地址ListNode* temp2 = cur->next->next->next;//1号节点连接3号节点cur->next = cur->next->next;//将3号节点连接上2号节点cur->next->next = temp1;//将2号节点的连接4号节点cur->next->next->next = temp2;//cur移动两位，准备下一轮cur = cur->next->next;}return dummyNode->next;}
};

力扣.19删除链表倒数第n个节点

原题链接

难点分析

这道题遍历两次，一次找出链表长度，另一次定位删除的节点并删除，解决起来不难，难的是一次遍历就解决完成删除

完整代码

class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {//思路：使用双指针，只扫描一次链表//具体步骤：//（1）快指针从虚拟头节点开始，先移动n步//（2）然后快慢指针同时移动，直至快指针到达链表末尾ListNode* dummyHead = new ListNode(0);dummyHead->next = head;ListNode* fastIndex = dummyHead;ListNode* lowIndex = dummyHead;while(fastIndex->next != nullptr){//n--是先减1，最后会少移动一次if(n-- > 0)//快指针先向后移动n个位置fastIndex = fastIndex->next;else{fastIndex = fastIndex->next;lowIndex = lowIndex->next;}}//删除慢指针后面的一个节点ListNode* temp = new ListNode();temp = lowIndex->next;lowIndex->next = temp->next;delete temp;return dummyHead->next;}
};

力扣142.环形链表

原题链接

难点分析：

（1）这道题用哈希法比较容易解决：持续向后遍历链表节点，如果同一个链表节点（这里的相同指的是存储节点的地址及地址中的内容都相同）出现了两次，那么就是环的入口节点。
（2）哈希法是一种“空间换时间”的解法，需要借助额外的空间，空间复杂度：O(N))，其中 N 为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。
（3）除此了哈希法，还可以借助逻辑推导，不借助额外的空间，这是力扣官方题解中的一种解法。

完整代码：

哈希法：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {//思路：哈希法//第一个遍历到的键就是环的起点unordered_set<ListNode*> mySet;ListNode* dummyHead = new ListNode(0);dummyHead->next = head;ListNode* cur = dummyHead;while(cur->next != NULL){if(mySet.count(cur->next)){return cur->next;}mySet.insert(cur->next);cur = cur->next;}return NULL;}
};

逻辑推导+快慢指针

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {//快慢指针法+公式推导//快慢指针法（双指针）常常被用来解决寻找环的入口、寻找两序列公共尾部入口、寻找距离尾部的第n个节点的问题//a = c + （n-1）*（b+c）：表明在到达相遇点后，如果有一个点从头节点出发，一步一步走，相遇的位置就是环的入口ListNode* fast = head;ListNode* slow = head;//寻找快慢指针的相遇点, 相遇后自动退出循环，即退出循环时，fast指针和slow指针在它们第一次相遇的节点上while(true){//如果还没有相遇就到达了链表尾部，表明这是一个无环的链表//情况1是空链表，情况2是链表中只有一个节点if(fast == nullptr || fast->next ==nullptr){return nullptr;}//有环，但是还没有相遇，继续走fast = fast->next->next;slow = slow->next;if(fast == slow) break;}//可以执行后面的代码说明一定有环//定义一个指针从头开始与slow同距离运动ListNode* ptr = head; //可以与slow同距离，也可以是fast//ptr和slow相遇的节点就是环的入口节点while(ptr != slow){ptr = ptr->next;slow = slow->next;}return ptr;}
};

三、感受与思考

前几天在接受字节客户端一面时，遇到了k组翻转链表的问题，在面试小哥的提示下用栈写出来了，但不知道能不能AC，痛定思痛，这一两周把《代码随想录》中的链表题目都做完了。
链表涉及的题型目前我主要了解了几种：

• 翻转链表
• 链表的环
• 链表节点的增删改查
• 两个链表的关系

在做题时，应当考虑链表的边界处理，考虑引入数据结构协助问题的解决，考虑引入双指针（快慢指针）。如果要充分锻炼自己，还要尝试使用数学推导，以思考换空间和时间。