论文复现丨多车场带货物权重车辆路径问题：改进邻域搜索算法

引言

本系列文章是路径优化问题学习过程中一个完整的学习路线。问题从简单的单车场容量约束CVRP问题到多车场容量约束MDCVRP问题，再到多车场容量+时间窗口复杂约束MDCVRPTW问题，复杂度是逐渐提升的。

如果大家想学习某一个算法，建议从最简单的TSP问题开始学习，一个阶梯一个阶梯走。

如果不是奔着学习算法源码的思路，只想求解出个结果，请看历史文章，有ortools、geatpy、scikit-opt等求解器相关文章，点击→路径优化历史文章，可直接跳转。

本系列文章汇总：

1、路径优化历史文章
2、路径优化丨带时间窗和载重约束的CVRPTW问题-改进遗传算法：算例RC108
3、路径优化丨带时间窗和载重约束的CVRPTW问题-改进和声搜索算法：算例RC108
4、路径优化丨复现论文-网约拼车出行的乘客车辆匹配及路径优化
5、多车场路径优化丨遗传算法求解MDCVRP问题
6、论文复现详解丨多车场路径优化问题:粒子群+模拟退火算法求解
7、路径优化丨复现论文外卖路径优化GA求解VRPTW
8、多车场路径优化丨蚁群算法求解MDCVRP问题
9、路径优化丨复现论文多车场带货物权重车辆路径问题：改进邻域搜索算法

问题描述

多车场带货物权重车辆路径问题可描述为：多个车场、每个中心有若干车辆、存在若干需求点、车辆从车场往返服务需求点。其中：车辆存在载重约束，数量约束。本文假设：

（1）需求点需求量已知，多个车场的车辆能满足服务要求;
（2）需求点位置已知，不考虑在需求点的服务时间;
（3）所有车辆型号和载重相同;
（4）配送车辆从车场出发，最终返回车场。一个需求点只能被访问一次。

详细描述见参考文献

数学模型

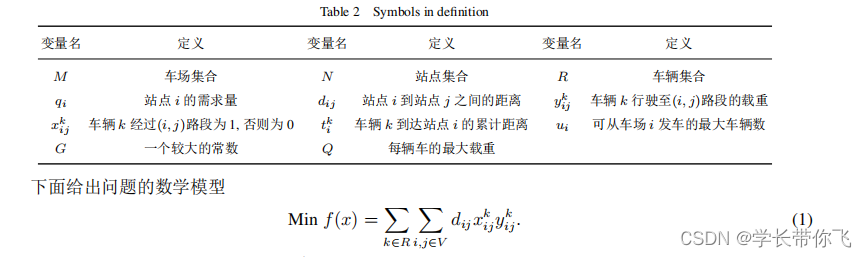
模型

具体模型见参考文献，目标函数是车辆运行距离和载重的乘积。

在这里插入图片描述

数据

数据是RC101，100个需求点，拆分后留下坐标和需求量：
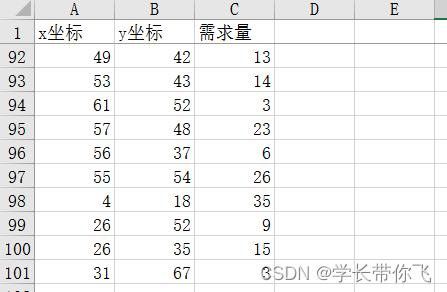
在这里插入图片描述

设计为3车场：
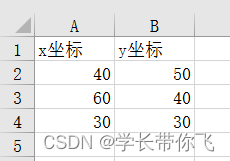
在这里插入图片描述

数据见网站：http://web.cba.neu.edu/~msolomon/rc101.htm

数据处理

pandas 读取对应列就行，比较简单。

def read():path = './data.xlsx'df = pd.read_excel(path, sheet_name = '需求点坐标')df1 = pd.read_excel(path, sheet_name = '车场')customer_x = df.iloc[:, 0].tolist()customer_y = df.iloc[:, 1].tolist()customer_demand = df.iloc[:, 2].tolist()center_x = df1.iloc[:, 0].tolist()center_y = df1.iloc[:, 1].tolist()return customer_x, customer_y, customer_demand, center_x, center_y

算法设计–编码解码

编码

论文的编码是用0到99的数表示100个点的位置，按照论文的编码生成方法：
在这里插入图片描述

计算各个车场到需求点的距离与需求点的比值，排序后依次挑选作为R条路径的起点，推文的车辆是15，R设为15，车辆0-5,5-10,10-15分别对应车场1,2,3 ，依次挑选各车场个车辆的初始点。

挑选完初始点后，再次计算gc值，挑选各车辆的剩余需求点，起点是对应车辆上一次访问的点，还需考虑载重约束：

def creat_init(self):cust_point = [i for i in range(len(self.x))]road_car = [[] for i in range(self.car_num)]idx1 = 0center_idx = 0abdan_id = []while cust_point:                               # 如果需求点Tabu集合非空if road_car[idx1] == []:                    # 如果某路径是空，起点是对应车场，文章车辆0-5,5-10,10-15分别对应车场1,2,3                               begin_x1, begin_y1 = self.x1[center_idx], self.y1[center_idx]else:                                       # 如何路径非空，起点是路径最后一个点，即上次访问的点begin_x1, begin_y1 = self.x[road_car[idx1][-1]], self.y[road_car[idx1][-1]]dist = [np.sqrt((self.x[k] - begin_x1)**2 + (self.y[k] - begin_y1)**2) for k in cust_point]gc = np.array(dist)/np.array(self.demand)[cust_point]# 距离及gc值计算id_all = np.array(cust_point)[gc.argsort()] # gc排序，得到对应从小到大的点idx3 = 0while sum(np.array(self.demand)[road_car[idx1] + [id_all[idx3]]]) > self.load:# 挑选的点必须满足载重约束，否则继续挑idx3 += 1if idx3 == len(id_all):                 # 如果所有剩余点都挑选完成，还不满足载重约束，认为该车辆的路径已经完成abdan_id.append(idx1)               # 记录该路径的索引，下次不用考虑breakif idx1 not in abdan_id:                    # 如果路径不是完成的路径，说明上面的while有结果idx2 = idx3road_car[idx1].append(id_all[idx2])     # 记录结果（挑选到的点）cust_point.remove(id_all[idx2])         # 移除Tabu集合对应点idx1 += 1if idx1 == self.every_num:                  # 如果车辆数达到5辆（每个车场5辆），车场更新center_idx += 1if idx1 == self.car_num:                    # 车辆计数归0             idx1 = 0return road_car

解码

上述方法生成的初始解：

[[68, 87, 54, 1, 5, 7, 71], [67, 69, 3, 45, 4, 2, 99], [79, 65, 85, 73, 74, 59, 60], [95, 53, 80, 37, 39, 38, 89], [64, 82, 98, 8, 14, 46, 41], [93, 70, 35, 34, 36, 40, 92], [49, 25, 26, 27, 31, 42, 43], [66, 18, 48, 24, 76, 6, 51], [91, 63, 22, 20, 77, 72, 61], [55, 75, 88, 47, 78, 44, 84], [83, 50, 17, 57, 15, 0], [21, 23, 19, 58, 16, 97], [94, 10, 9, 11, 13, 81], [33, 30, 28, 29, 32, 62], [90, 56, 96, 86, 12, 52]]

一个车辆的解码如下：

1、根据路径索引读出各点的坐标和需求；

2、计算第一个点到第二个点的距离（车场到第一个点的载重0，开销为0不考虑），载重取第一个点的载重（后面的载重依次累加），更新开销；

3、每辆车遍历到最后一个点时，计算点到车场的距离，载重取累积到最后一个点的载重，开销更新，解码结束：

代码如下：

def f_caculate(self, road_car):f_all = [0 for i in range(self.car_num)]for k in range(len(road_car)):road = road_car[k]                         # 每一辆车的路径load = 0center_idx = k//self.every_num             # 车场for j in range(1, len(road)):start, end = road[j - 1], road[j]      # 从第一个点开始，车场到第一个点载重是0，开销不考虑load += self.demand[start]begin_x, begin_y = self.x[start], self.y[start]end_x, end_y = self.x[end], self.y[end]f = np.sqrt((end_x - begin_x)**2 + (end_y - begin_y)**2)*load # 开销f_all[k] += f  start = road[-1]                          # 最后一个点回到车场的开销begin_x, begin_y = self.x[start], self.y[start]end_x, end_y = self.x1[center_idx], self.y1[center_idx]load += self.demand[start]f = np.sqrt((end_x - begin_x)**2 + (end_y - begin_y)**2)*loadf_all[k] += freturn f_all

邻域搜索算子设计

一、one-point move算子

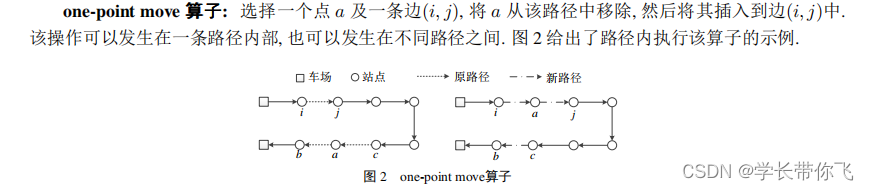
在这里插入图片描述

同路径：选择一个点随机插入该路径的任意位置

不同路径：选择一个点随机插入不同路径的任意位置

需注意的是：同路径不用考虑载重约束，不同路径需考虑载重约束，每个算子有while,为避免陷入死循环，设置10次没有新解生成就返回原解。所有算子不同路径考虑载重，最多10次迭代。

代码：

def one_point_move(self, road_car):count = 0while True:idx1 = random.randint(0, self.car_num-1)          # 选择一个路径if road_car[idx1]:a = random.choice(road_car[idx1])                 # 对应路径的一个需求点breakif count == 10:breakcount += 1road_car[idx1].remove(a)                          # 移除对应需求点demand_all = [sum(np.array(self.demand)[de]) for de in road_car] # 各条路径的载重计算location = [i for i in range(self.car_num) if demand_all[i] + self.demand[a] <= self.load]count = 0                                                       # 提取可加入改点的所有路径（载重可接受）while True and location:idx2 = random.choice(location)                    # 选择一个可接受路径if len(road_car[idx2])>0:insert_id = random.randint(0, len(road_car[idx2]) - 1) # 随机选择一个插入位置road_car[idx2].insert(insert_id, a)               # 需求点插入breakif count == 10:breakcount += 1return road_car

二、2-exchange算子

随机选择两条不同路径的两个点进行交换，不同路径考虑载重约束。

代码：

def exchange_2(self, road_car):signal = 1count = 0while signal:loc = random.sample(range(self.car_num),2)         # 不同的2条路径if len(road_car[loc[0]])>0 and len(road_car[loc[1]])>0:id1 = random.randint(0, len(road_car[loc[0]]) - 1) # 第一条路径选择一个点id2 = random.randint(0, len(road_car[loc[1]]) - 1) # 第二条路径选择一个点de1 = np.array(self.demand)[road_car[loc[0]]]      # 对应路径的载重（路径所有点）de2 = np.array(self.demand)[road_car[loc[1]]]d1 = self.demand[id1]                              # 第一个点的需求量                   d2 = self.demand[id2]                              # 第二个点的需求量if sum(de1)-d1 + d2 <= self.load and sum(de2)-d2 + d1 <= self.load:  # 如果2条路径交换后载重满足road_car[loc[0]][id1], road_car[loc[1]][id2] = road_car[loc[1]][id2], road_car[loc[0]][id1]signal = 0                                     # 更新并跳出循环if count == 10:breakcount += 1return road_car

三、2-opt算子
在这里插入图片描述

为了简化，把a,b,c,d看做位置索引，那么b = a+1，d = c+1

不同路径：路径一a前面的与d后面的合并成新路径，路径二c前面的与b后面的合并成新路径

同一路径：路径a前面与逆序bc路径相连，再与d后面路径相连。

同一路径不考虑载重约束，不同路径要考虑

代码：

def opt_2(self, road_car):signal = 1count = 0while signal:idx1 = random.randint(0, self.car_num - 1)         # 随机选择路径索引1idx2 = random.randint(0, self.car_num - 1)         # 随机选择路径索引1if len(road_car[idx1]) > 1 and len(road_car[idx2]) >1:a = random.randint(0, len(road_car[idx1]) - 2)     # 路径1生成索引a，-2是保证b存在b = a + 1                                          # b是a+1c = random.randint(0, len(road_car[idx2]) - 2)     # 生成索引b，-2是保证d存在d = c + 1                                          # d 是b+1if idx1 == idx2:                                   # 如果同一路径if a > c:                                      # 如果a 索引大于ca, b, c, d = c, d, a, b                    # 交换a,b 和 c,dro = road_car[idx1]                           r = ro[b:c+1]                                  # b到c的路径if r:                                          # 如果存在，逆序r.reverse()road = ro[:a+1] + r + ro[d:]                   # 重新连接得到新路径road_car[idx1] = road                          # 更新路径signal = 0else:                                              # 如果是不同路径ro1, ro2 = road_car[idx1], road_car[idx2]road1 = ro1[:a+1] + ro2[d:]                    # 对应路径截取相连road2 = ro2[:c+1] + ro1[b:]if sum(np.array(self.demand)[road1]) <= self.load and sum(np.array(self.demand)[road2]) <= self.load:road_car[idx1] = road1                     # 如果满足载重，更新2条路径road_car[idx2] = road2signal = 0if count == 10:breakcount += 1return road_car

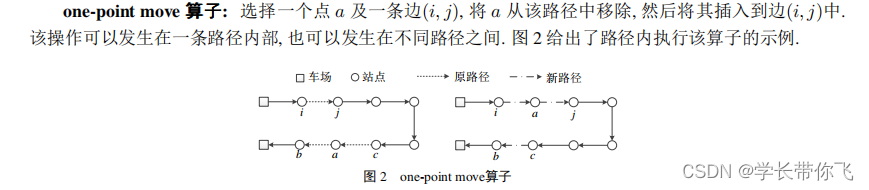
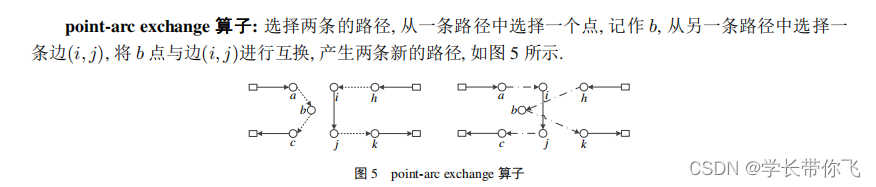
四、point-arc exchange算子

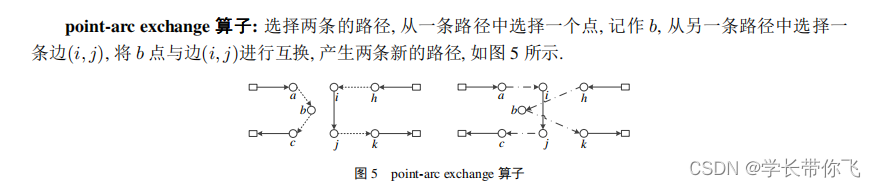
在这里插入图片描述

生成不同的路径，分别挑选点b 和点i,j，考虑载重约束同时进行交换

代码：

def point_arc_exchange(self, road_car):signal = 1count = 0while signal:loc = random.sample(range(self.car_num), 2)        # 生成不相同的2条路径索引id1, id2 = loc[0], loc[1]road1, road2 = road_car[id1], road_car[id2]if len(road1)>0 and len(road2)>1:idx1 = random.randint(0, len(road1) - 1)           # 第一条路径随机生成位置b = road1[idx1]                                    # 取对应位置的点idx2 = random.randint(0, len(road2) - 2)           # 第而条路径随机生成位置，-2是为了idx2 + 1可行i, j = road2[idx2], road2[idx2 + 1]                # 取2个点i,jroad1.insert(idx1, i)                              # 插入点iroad1.insert(idx1 + 1, j)                          # 插入点jroad1.remove(b)                                    # 路径1移除broad2.insert(idx2, b)                              # 路径2插入b                    road2.remove(i)                                    # 移除iroad2.remove(j)                                    # 移除jif sum(np.array(self.demand)[road1]) <= self.load and sum(np.array(self.demand)[road2]) <= self.load:road_car[id1] = road1                          # 如果2条路径都满足载重约束，更新，跳出循环road_car[id2] = road2signal = 0if count == 10:breakcount += 1return road_car

五、or-opt算子
在这里插入图片描述

选择不同路径，在载重约束下把一条路径的一段路线插入另一段。

def or_opt(self, road_car):count = 0while 1:idx1 = random.randint(0, self.car_num-1)            # 选择一条路径索引road1 = road_car[idx1]if len(road1) <= 2:breakloc =random.sample(range(len(road1)),2)             # 路径生成2个位置loc.sort()                                          # 升序uv = road1[loc[0]:loc[1]]                           # 截取插入的编码demand_all = [sum(np.array(self.demand)[de]) for de in road_car]location = [i for i in range(self.car_num) if demand_all[i] + sum(np.array(self.demand)[uv])<= self.load and i != idx1]                     # 载重约束生成可插入的车辆路径（不包括上面路径）if location:                                        # 如果可插入路径非空idx2 = random.choice(location)road2 = road_car[idx2]road1 = road1[:loc[0]] + road1[loc[1]:]         # 路径1截取剩下的路线if len(road2)>0:id2 = random.randint(0, len(road2) - 1)         # 路径2的插入位置road2 = road2[:id2] + uv + road2[id2:]          # 路径2更新road_car[idx1] = road1road_car[idx2] = road2breakif count == 10:breakcount += 1return road_car

六、cross-exchange算子

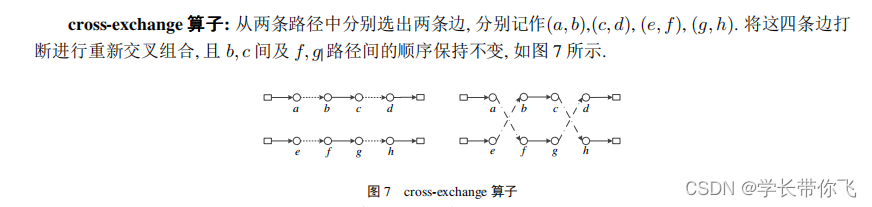
不同路径之间，分别生成b,c和f,g，在载重约束下互相交换

代码：

def cross_exchange(self, road_car):signal = 1count = 0while signal:loc = random.sample(range(self.car_num),2)          # 生成不重复的2个路径索引loc.sort()                                          # 升序id1, id2 = loc[0], loc[1]road1, road2 = road_car[id1], road_car[id2]if len(road1)>1 and len(road2)> 1 :                 # 保证b,c,f,g都存在idx1 = random.randint(0, len(road1) - 2)        # 第一个路径生成b和c，-2是保证idx1 + 1可行b = road1[idx1]c = road1[idx1 + 1]idx2 = random.randint(0, len(road2) - 2)         # 第二个路径生成f和g，-2是保证idx2 + 1可行f = road2[idx2]g = road2[idx2 + 1]road1.insert(idx1, f)                            # 互相交换road1.insert(idx1 + 1, g)road1.remove(b)road1.remove(c)road2.insert(idx2, b)road2.insert(idx2 + 1, c)road2.remove(f)road2.remove(g)if sum(np.array(self.demand)[road1]) <= self.load and sum(np.array(self.demand)[road2]) <= self.load:road_car[id1] = road1                           # 2条路径都满足约束时更新，并跳出循环                      road_car[id2] = road2signal = 0if count == 10:breakcount += 1return road_car

七、3-opt算子
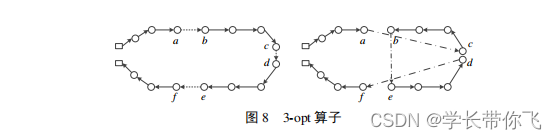
在这里插入图片描述

挑选3条边，做2次2-opt操作：

def opt_3(self, road_car):count = 0while True:idx = random.randint(0, self.car_num-1)                     # 选择一条路径索引if len(road_car[idx]) >= 4:                                         # 保证a,b,c,d都存在loc = random.sample(range(len(road_car[idx]) - 1),3)    # 生成不重复的3个路径索引loc.sort()                                              # 升序road = road_car[idx]                                    # 依次当作a,b,c,d,e,f的位置索引id_a, id_b = loc[0], loc[0] + 1id_c, id_d = loc[1], loc[1] + 1id_e, id_f = loc[2], loc[2] + 1r1 = road[id_b:id_c + 1]                                # r1非空时逆序，即id_b不等于id_cif r1:r1.reverse()r2 = road[id_d:id_e + 1]                                # r2非空时逆序，即id_d不等于id_e  if r2:r2.reverse()                  road = road[:id_a + 1] + r1 + r2 + road[id_f:]          # 重构road_car[idx] = roadbreakif count == 10:breakcount += 1return road_car

邻域搜索算法设计

在这里插入图片描述

k次扰动主要是利用邻域搜索算法对初始解进行寻优，接受gbest（1+ range）的解：

ges\image-20240407190756731.png)

def algorithm1(self,road_car, gbest, ran, T_roadcar, answer):road_car1 = self.mo.one_point_move(road_car)              # 第一个算子得到新路径f = sum(self.cd.f_caculate(road_car1))                    # 新路径的开销if f < gbest*(1 + ran):                                   # 结束解的范围T_roadcar.append(copy.deepcopy(road_car1))            # 记录解，copy是防止变量的相互引用，引起路径的变化answer.append(f)                                      # 记录开销，road_car1 = self.mo.exchange_2(road_car1)                 # 下面同上f = sum(self.cd.f_caculate(road_car1))if f < gbest*(1 + ran):T_roadcar.append(copy.deepcopy(road_car1))answer.append(f)road_car1 = self.mo.opt_2(road_car1)f = sum(self.cd.f_caculate(road_car1))if f < gbest*(1 + ran):T_roadcar.append(copy.deepcopy(road_car1))answer.append(f)road_car1 = self.mo.point_arc_exchange(road_car1)f = sum(self.cd.f_caculate(road_car1))if f < gbest*(1 + ran):T_roadcar.append(copy.deepcopy(road_car1))answer.append(f)road_car1 = self.mo.or_opt(road_car1)f = sum(self.cd.f_caculate(road_car1))if f < gbest*(1 + ran):T_roadcar.append(copy.deepcopy(road_car1))answer.append(f)road_car1 = self.mo.cross_exchange(road_car1)f = sum(self.cd.f_caculate(road_car1))if f < gbest*(1 + ran):T_roadcar.append(copy.deepcopy(road_car1))answer.append(f)road_car1 = self.mo.opt_3(road_car1)f = sum(self.cd.f_caculate(road_car1))if f < gbest*(1 + ran):T_roadcar.append(copy.deepcopy(road_car1))answer.append(f)return T_roadcar, answer

步骤3的邻域搜索：接受更好的解

步骤2得到一组解时，步骤3分别寻优，寻优时把algorithm1(self,road_car, gbest, ran, T_roadcar, answer)的

road_car设置为各个解的路径，gbest设置为各个解的开销，ran设置为0

其余步骤同上面算法步骤相同。代码太冗杂，运行速度慢，没再考虑perturb2 。

def msil(self):f = self.cd.f_caculate(self.road_car_init)gbest = sum(f)result = [[], []]for I in range(self.Max_I):                         # 算法步骤6if I == 0:road_car = copy.deepcopy(self.road_car_init)print(f'第{I}次迭代的最小开销是：{gbest}')result[0].append(I)result[1].append(gbest)H = 0T_roadcar, answer = [], []while H < self.Max_H:road_car2 = copy.deepcopy(road_car)          # 备份road_car，否则下面算子操作会引起road_car变化k = random.randint(self.car_num, self.car_num*2)for kk in range(k):                          # k次扰动，对应算法步骤2T_roadcar,answer = self.algorithm1(road_car,gbest,self.ran,T_roadcar,answer)T_roadcarx = copy.deepcopy(T_roadcar)road_car = road_car2                         # road_car再赋值signal = 0if answer:                                   # 如果扰动得到一组新解count = 0for car_ro in T_roadcarx:                # 每个新解寻优fx = answer[count]T_roadcar1, answer1 = [], []T_roadcar1, answer1 = self.algorithm1(car_ro,fx,0,T_roadcar1,answer1)if T_roadcar1:                       # 如果新解得到改进，一个解的算法步骤3结束if min(answer1) < gbest:         # 比较改进的解和gbestgbest = min(answer1)idx = answer1.index(min(answer1))road_car = T_roadcar1[idx]signal = 1                   # 如果比gbest还优秀，更新gbest并赋值signal为1count += 1if signal == 1:                              # gbest更新时H赋值1否则H++,对应算法步骤5H = 1else:H += 1print(f'第{I+1}次迭代的最小开销是：{gbest}')result[0].append(I)result[1].append(gbest)return road_car, result

结果

代码运行环境
windows系统，python3.6.0,第三方库及版本号如下：

numpy==1.18.5
matplotlib==3.2.1

第三方库需要在安装完python之后，额外安装，以前文章有讲述过安装第三方库的解决办法。

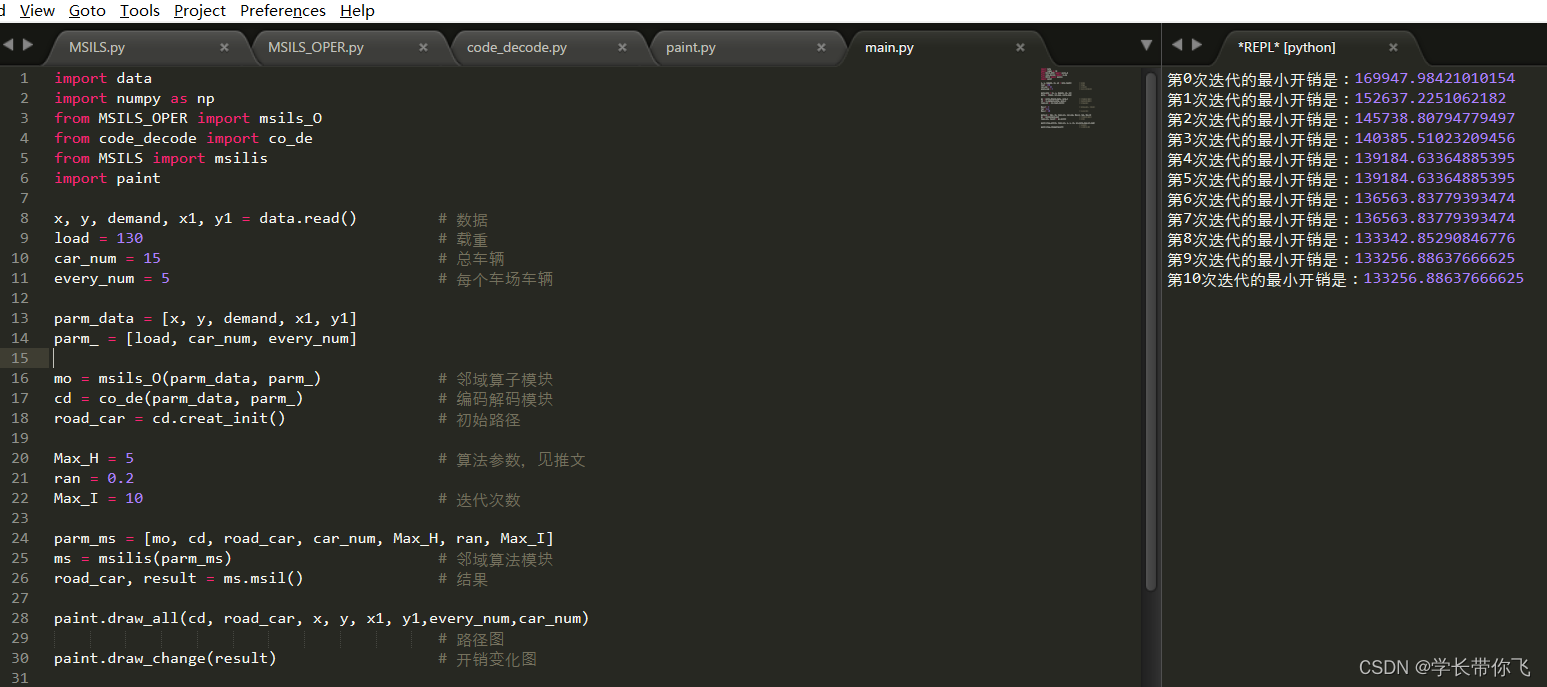
主函数

设计主函数如下：

import data
import numpy as np
from MSILS_OPER import msils_O
from code_decode import co_de
from MSILS import msilis
import paintx, y, demand, x1, y1 = data.read()         # 数据
load = 130                                 # 载重
car_num = 15                               # 总车辆               
every_num = 5                              # 每个车场车辆parm_data = [x, y, demand, x1, y1]
parm_ = [load, car_num, every_num]mo = msils_O(parm_data, parm_)             # 邻域算子模块
cd = co_de(parm_data, parm_)               # 编码解码模块
road_car = cd.creat_init()                 # 初始路径Max_H = 5                                  # 算法参数，见推文
ran = 0.2
Max_I = 10                                 # 迭代次数                    parm_ms = [mo, cd, road_car, car_num, Max_H, ran, Max_I]
ms = msilis(parm_ms)                       # 邻域算法模块
road_car, result = ms.msil()               # 结果paint.draw_all(cd, road_car, x, y, x1, y1,every_num,car_num)# 路径图
paint.draw_change(result)                  # 开销变化图

运行结果

结果如下：

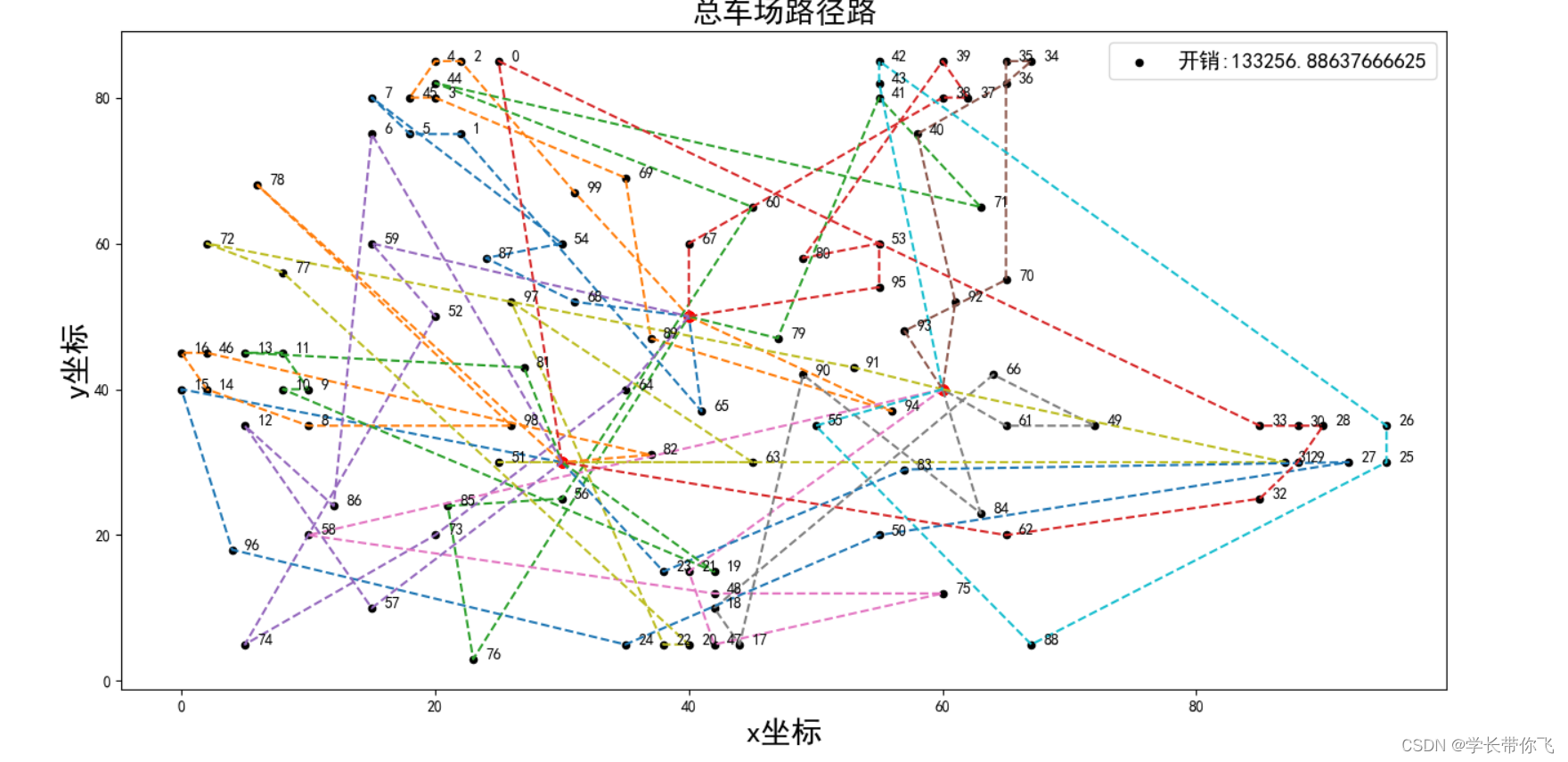
在这里插入图片描述

总路径图：
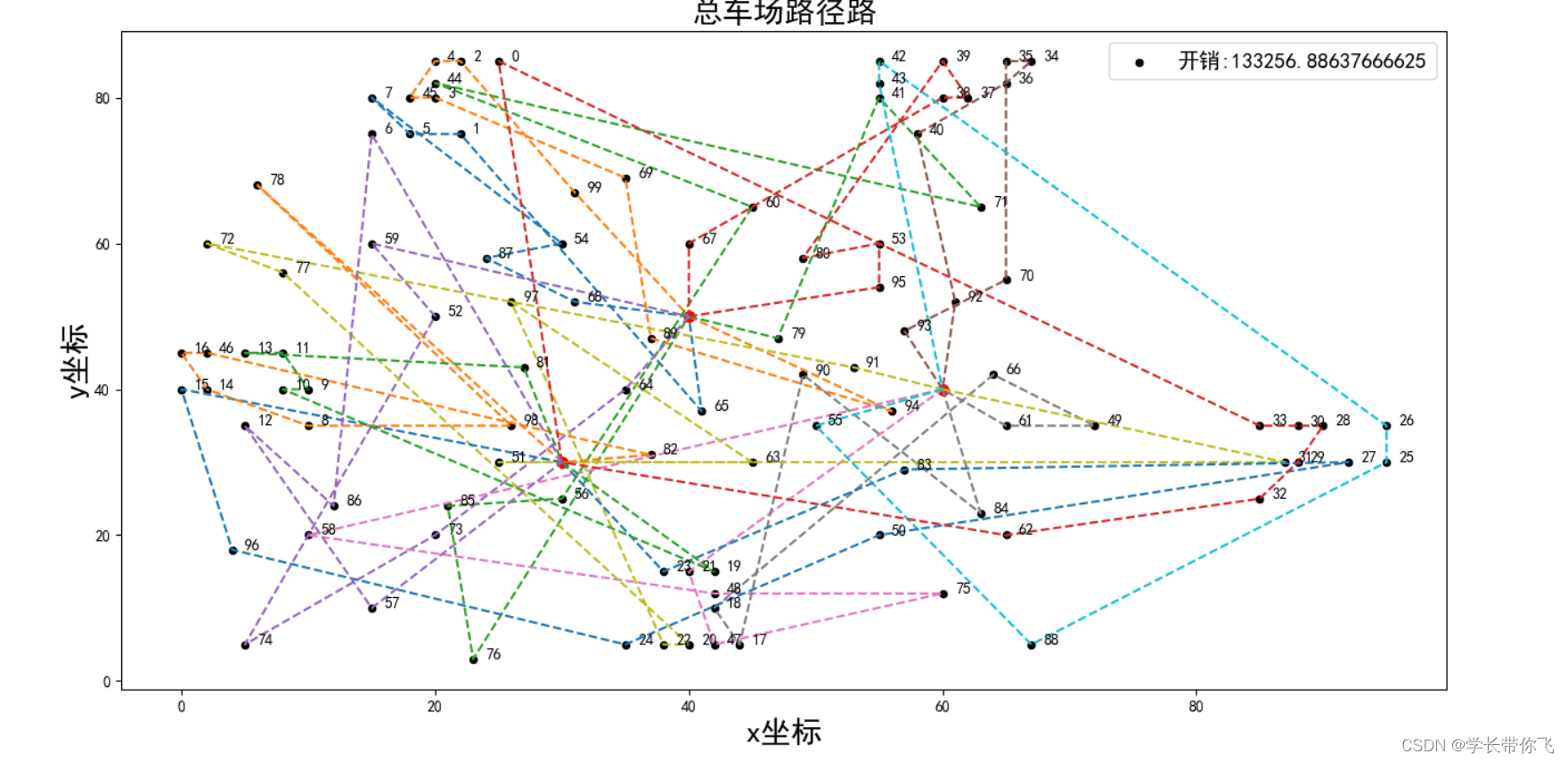
在这里插入图片描述

车场1
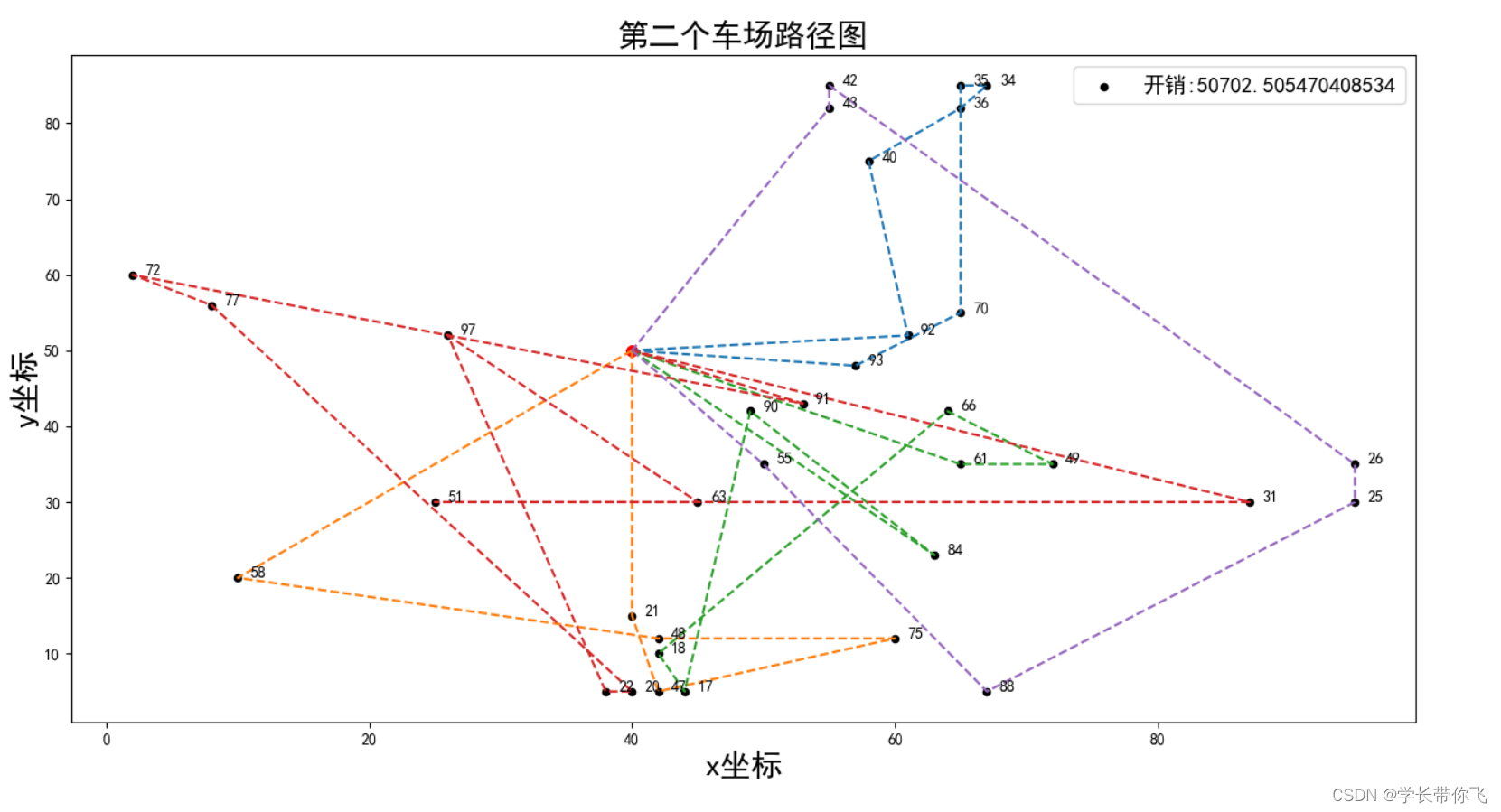
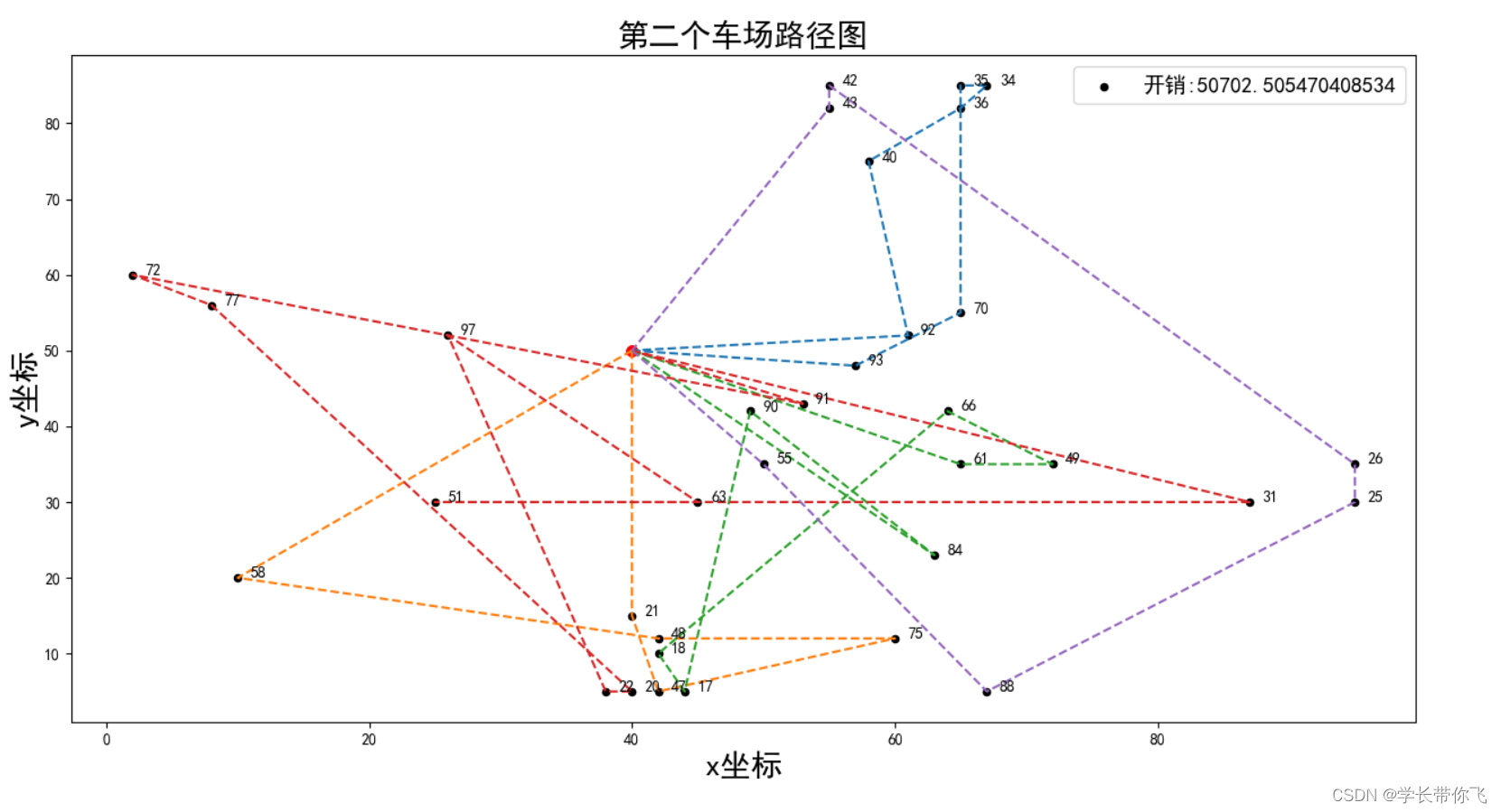
在这里插入图片描述

车场2
在这里插入图片描述

车场3
在这里插入图片描述

成本随迭代次数的变化图如下：
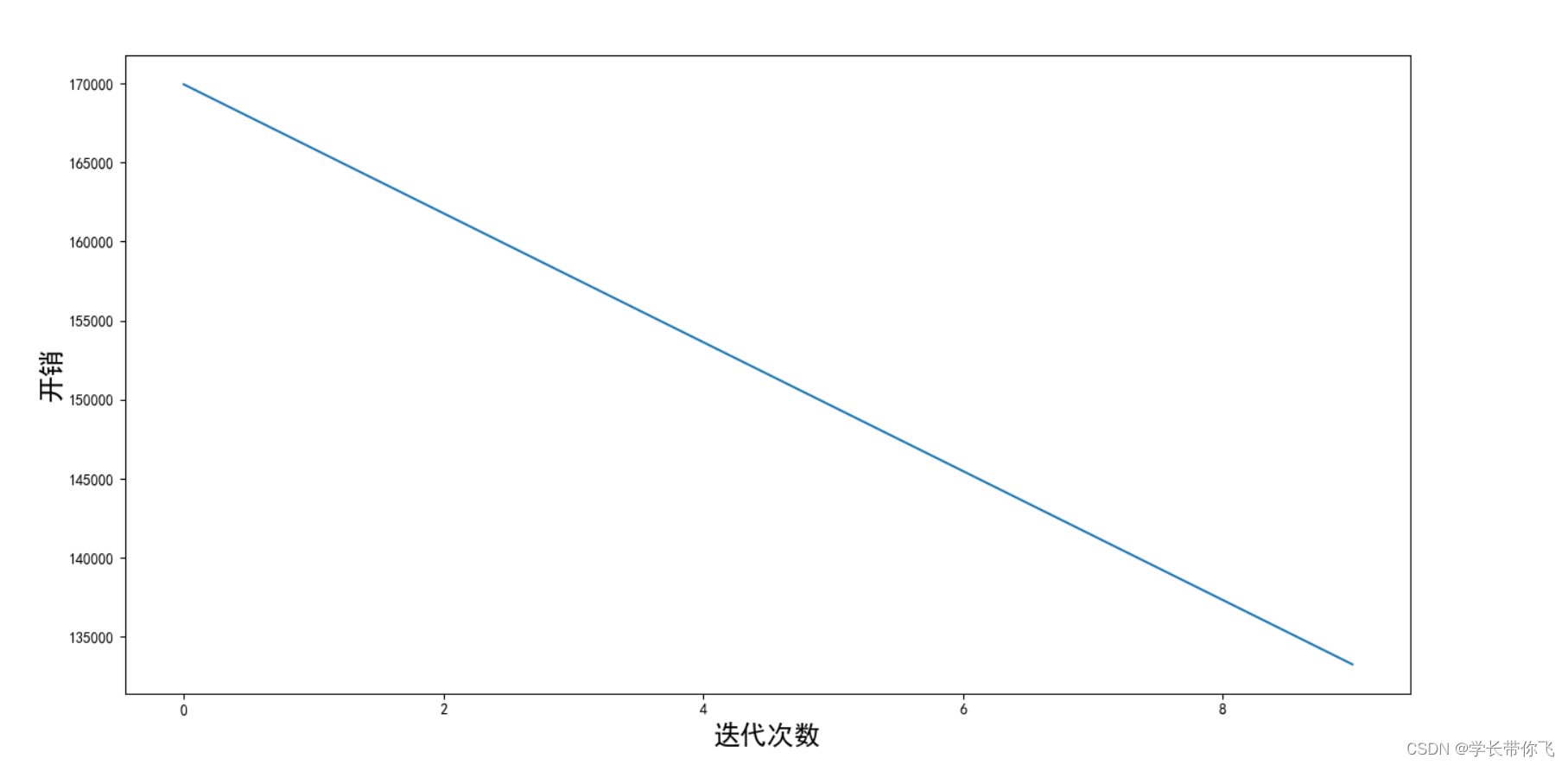
在这里插入图片描述

还有优化空间，增大迭代次数试试。

结论

本推文主要是对参考论文进行复现，也有自己的小设计，但基本是复现原文，具体算法步骤见文献，不做过多介绍。

数据采用rc101，可修改数据

参考文献：
[1]王新玉,唐加福,邵帅.多车场带货物权重车辆路径问题邻域搜索算法[J].系统工程学报,2020,35(06):806-815.DOI:10.13383/j.cnki.jse.2020.06.008.

代码

为了方便，把代码浓缩在3个代码里，excel数据生成后每次运行main.py无需再运行data_collect().txt_to_xlsx() 。

演示视频：

论文复现丨多车场带货物权重车辆路径问题：改进邻域搜索算法

文末

完整算法+数据：
完整算法源码+数据：见下方微信公众号：关注后回复：调度

# 微信公众号：学长带你飞
# 主要更新方向：1、柔性车间调度问题求解算法
#              2、学术写作技巧
#              3、读书感悟
# @Author  : Jack Hao