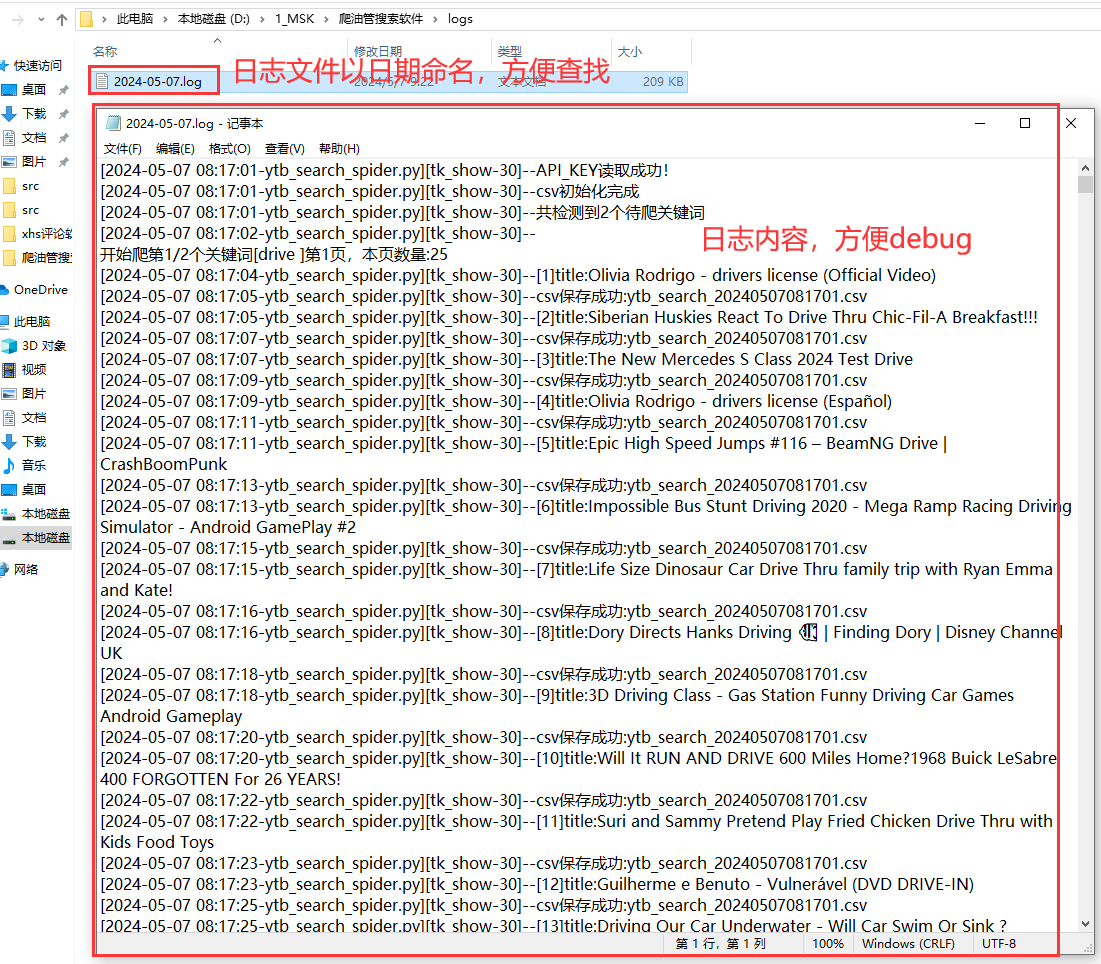
编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：

首先需要将给出的数值进行拆分：
 

bool isHappy(int n) {int r = 0;n = 15646;while(n != 0){int d= n  % 10;n /= 10;  //r += d * d;printf("%d\n",d);}// printf("%d\n",r);return false;
} 

之后开始按照题目对其计算平方和，将代码封装起来

int next_n(int n)
{int r = 0;while(n != 0){int d= n % 10;n /= 10;  r += d * d;printf("%d\n",d);}return r;
}
bool isHappy(int n) 
{n = next_n(n);  printf("%d\n",n);return true;
} 

之后加上条件判断，当该数之前出现过时，则退出循环，未出现过则继续

int next_n(int n)
{int r = 0;while(n != 0){int d= n % 10;n /= 10;  r += d * d;}return r;
}
bool contains(int *history, int size , int n)
{for(int i = 0; i < size ; i++ ){if(history[i] ==n )return true;}return false;}
bool isHappy(int n) 
{int history[10000];int size = 0;while(!contains(history, size , n)){history[size] = n;size++;n = next_n(n);}  return n == 1;
} 

中间添加了一个条件判断，需要判断该数在之前有没有出现过。

实际上history最大只有9*9*10次，即810；

之后简化算法，利用龟兔赛跑，寻找重复数

int next_n(int n)
{int r = 0;while(n != 0){int d= n % 10;n /= 10;  r += d * d;}return r;
}bool isHappy(int n) 
{int slow = n;int fast = n;do{slow = next_n(slow);fast = next_n(fast);fast = next_n(fast);} while(slow != fast);return fast == 1;
}