如何理解kmp的套娃式算法啊？

概念

KMP算法，全称Knuth Morris Pratt算法。文章大部分内容出自《数据结构与算法之美》

核心思想

假设主串是a，模式串是b

在模式串与主串匹配的过程中，当遇到不可匹配的字符的时候，对已经对比过的字符，是否能找到一种规律，将模式串一次性滑动多位，跳过那些肯定不会匹配的情况？

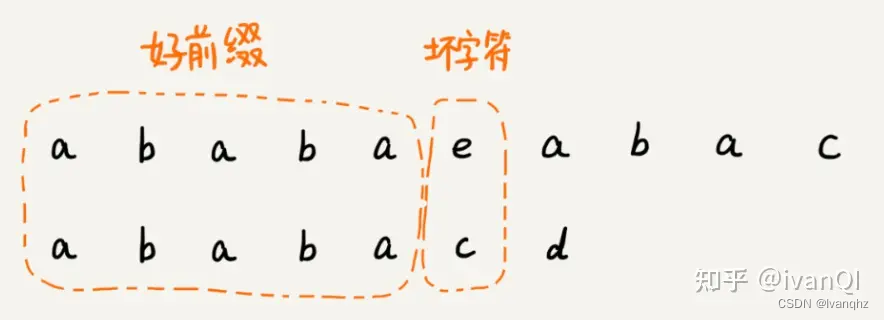
在这里插入图片描述

这里可以类比一下，在模式串和主串匹配的过程中,把不能匹配的那个字符仍然叫做坏字符，把已经匹配的那段字符串叫做好前缀

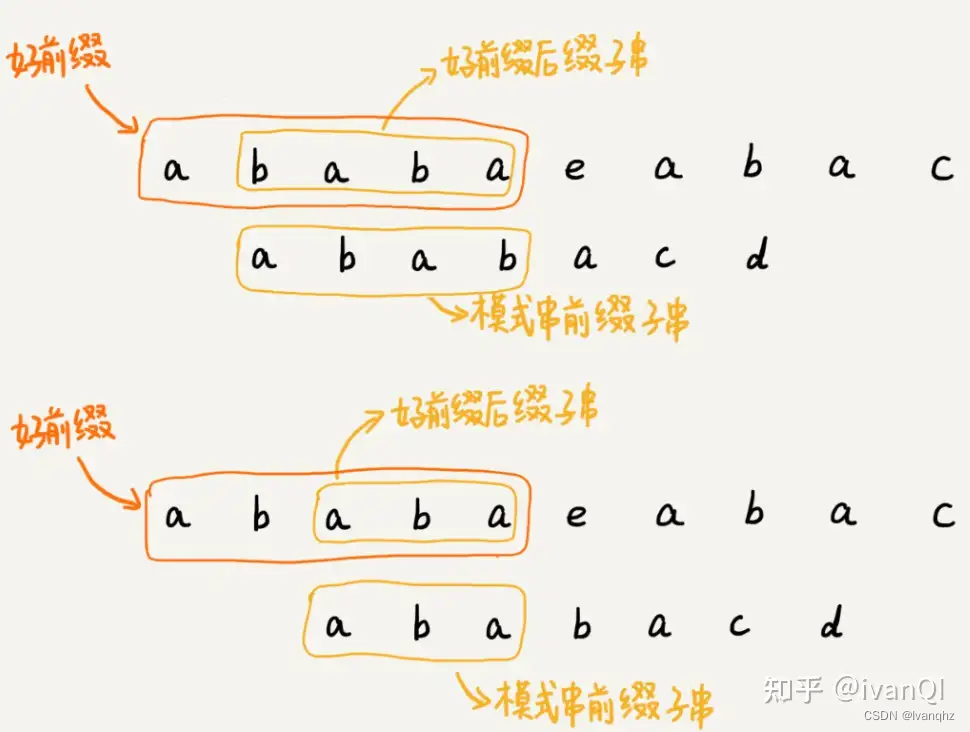
在这里插入图片描述
当遇到坏字符的时候，就要把模式串往后滑动，在滑动的过程中，只要模式串和好前缀有上下重合，前面几个字符比较，就相当于拿好前缀的后缀子串，跟模式串的前缀子串在比较

KMP目的

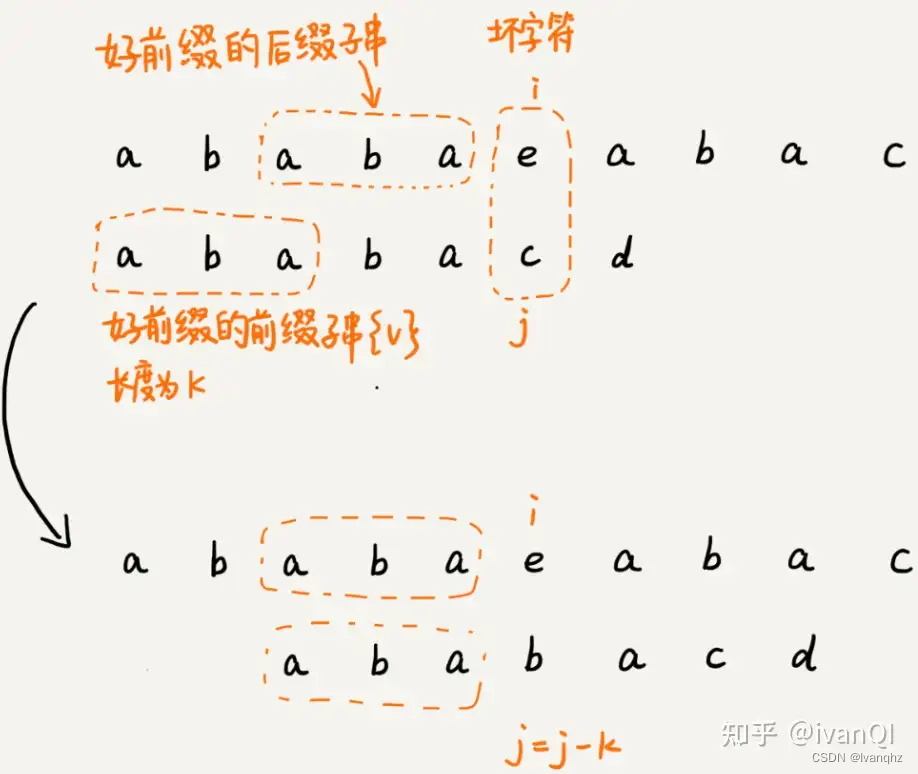
在这里插入图片描述
只需要拿好前缀本身，在它的后缀子串中，查找最长的那个可以跟好前缀匹的前缀子串匹配

假设最长的可匹配的那部分前缀子串{v}, 长度为k

可以把模式串一次性往后滑动j - k位，相当于，每次遇到坏字符的时候，就把j 更新为k。i不变。然后比较

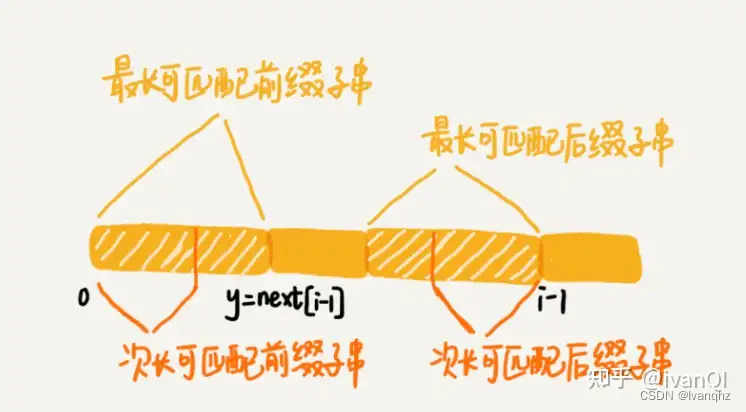
最长可匹配后缀子串 && 最长可匹配前缀子串

把好前缀的所有后缀子串中，最长的可匹配前缀子串的那个后缀子串，叫作最长可匹配后缀子串

对应的前缀子串，叫作最长可匹配前缀子串

在这里插入图片描述
为什么求最长可匹配子串前缀和后缀子串，为什么不涉及主串，只需通过模式串就能求解？

以上图所示，好前缀的定义是主串和模式串匹配的部分
所以好后缀的最长可匹配子串必然会落到模式串中，所以用模式串求最长可匹配的前缀和后缀子串

失效函数(next 数组)

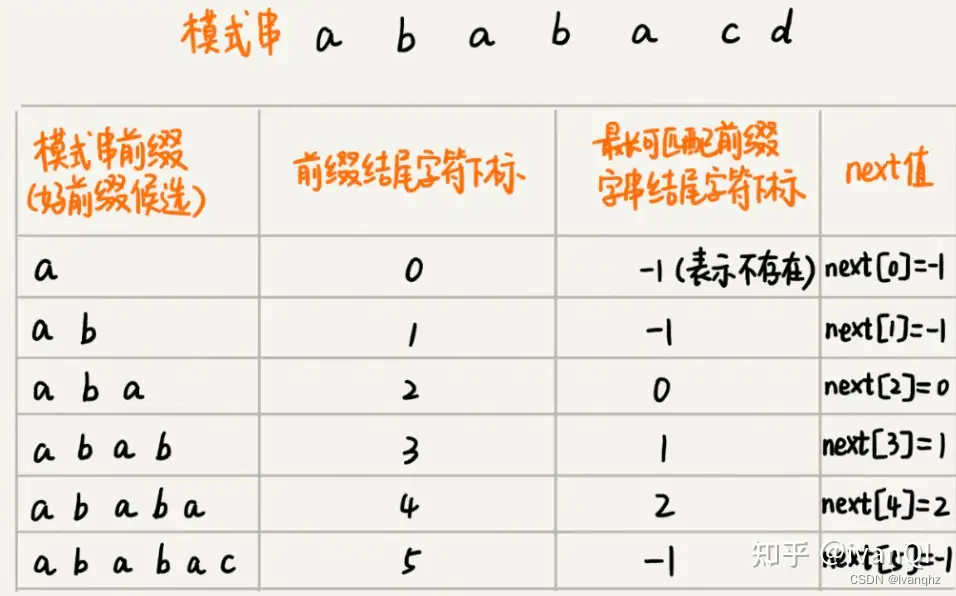
在这里插入图片描述
数组的下标是每个前缀结尾字符下标，数组的值是这个

前缀的最长可以匹配前缀子串的结尾字符下标

例子：ababacd

前缀列表访问顺序：从右到左
后缀列表访问顺序：从左到右
过程

1. a: 无匹配，下标为-1
2. ab: 无匹配，下标为-1
3. aba: 匹配1个字符。下标为0前缀： a ab后缀： ba a
4. abab，匹配2个字符，下标为1前缀：a ab aba后缀：bab ab b
5. ababa，匹配3个字符，下标为2前缀：a ab aba abab后缀：baba aba ab a
6. ababac，无匹配，下标为-1前缀：a ab aba abab ababa后缀：babac abac bac ac c
7. ababacd，无匹配，下标为-1前缀：a ab aba abab ababa ababac后缀：babacd abacd bacd acd cd c

next数组的计算

暴力计算方法

暴力求解子串，效率低
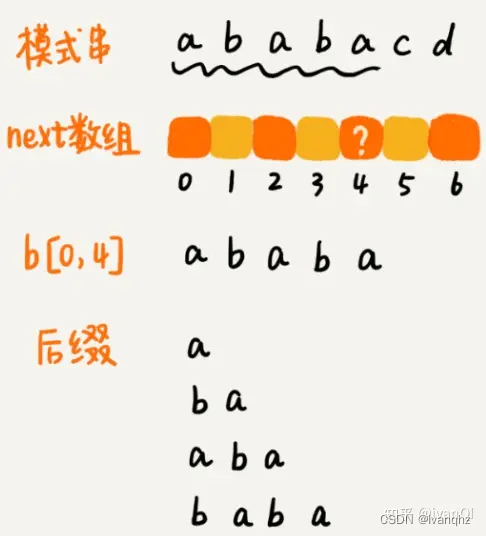
在这里插入图片描述
把所有后缀子串从长到短找出来，依次看能否匹配前缀

类动态规划方法(k：最长前后缀子串)

若p[k] == p[i]

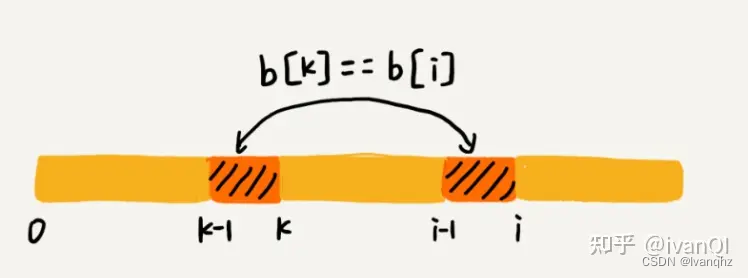
在这里插入图片描述
如果 next[i - 1] = k - 1，那么子串 b[0, k - 1] 是 b[0, i - 1]最长可匹配前缀子串

如果子串 b[0, k - 1] 的下一个字符 b[k]，与 b[0, i -1 ]的下一个字符 b[i] 匹配，那子串 b[0, k]就是 b[0, i]的最长可匹配前缀子串

若p[k] ≠ p[i]

假设最长可匹配前缀 k

如果 p[k] ≠ p[i]。则需要次最大匹配前缀 p[next[k]].

如果 p[next[k]] ≠ p[i]. 则需要次次最大匹配前缀。直到匹配成功，或者匹配失败
在这里插入图片描述

代码地址

数据结构和算法

时间复杂度

构建next数组

void getNext(char *p, int p_len, int *next) {next[0] = -1;int k = -1;int i;for (i = 1; i < p_len; ++i) {while (k != -1 && p[k + 1] != p[i]) {k = next[k];}if (p[k + 1] == p[i]) {++k;}next[i] = k;}}

i 从1开始一直增加到p_len,而k并不是每次for循环都增加，所以，k累积增加的值肯定小于 p_len

而while循环中的 k = next[k],实际上是在减小k的值，k累积都没有增加超过p_len.所以while循环总数也不会超过p_len

这部分时间复杂度: O(p_len)

借助next数组匹配

int kmp(char *s, int s_len, char *p, int p_len) {int next[p_len];getNext(p, p_len, next);int j = 0;int i;for (i = 0; i < s_len; ++i) {while (j > 0 && s[i] != p[j]) { // 一直找到s[i] 和 p[j]j = next[j - 1] + 1;}if (s[i] == p[j]) ++j;if (j == p_len) {   // 找到匹配模式串return i - p_len + 1;}}return -1;
}

i 从0循环增加到 s_len - 1, j的增长量不可能超过i，所以肯定小于s_len

而while 循环中的那条 j = next[j - 1] + 1; 不会让 j增长

所以，这部分的时间复杂度为O(s_len)

总时间复杂度: O(s_len + p_len)