这套题挺简单的。。。

A题 AC率差不多100%
B题 AC率差不多75%
C题 AC率也差不多75%
D题 AC率 50%
E题 AC率 25%
向着top 1%出发
A题题解
Stair, Peak, or Neither?
简单判断题,自己写
#include<bits/stdc++.h>
using namespace std;
int A[5];
int main() {int t;scanf("%d",&t);while(t--){for(int i=1;i<=3;i++){scanf("%d",&A[i]);}if(A[1]<A[2]&&A[2]<A[3]){printf("STAIR\n");}else if(A[1]<A[2]&&A[2]>A[3]){printf("PEAK\n");}else{printf("NONE\n");}}return 0;
}
B题题解
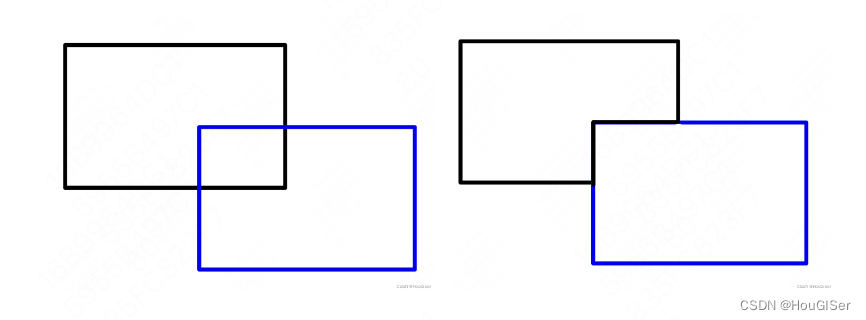
找规律,算出每个矩形的最左上角坐标不就可以填充了
#include<bits/stdc++.h>
using namespace std;
char s[45][45];
int main() {int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);int op=0;for(int i=1;i<=n;i++){if(i%2)op=0;else op=1;for(int j=1;j<=n;j++){if(op%2==1){s[i*2-1][j*2-1]='.';s[i*2-1][j*2]='.';s[i*2][j*2-1]='.';s[i*2][j*2]='.';op=(op+1)%2;}else{s[i*2-1][j*2-1]='#';s[i*2-1][j*2]='#';s[i*2][j*2-1]='#';s[i*2][j*2]='#';op=(op+1)%2;}}}for(int i=1;i<=2*n;i++){for(int j=1;j<=2*n;j++){printf("%c",s[i][j]);}printf("\n");}}return 0;
}
C题题解
模拟题。。没啥好说的,认真读题
#include<bits/stdc++.h>
using namespace std;
int main() {int t;scanf("%d",&t);while(t--){int a,b;scanf("%d:%d",&a,&b);if(a<12){if(a==0)printf("12");else if(a<10)printf("0%d",a);else printf("%d",a);printf(":");if(b<10)printf("0%d",b);else printf("%d",b);printf(" AM\n");}else{if(a>12){a=a%12;}if(a==0)printf("12");else if(a<10)printf("0%d",a);else printf("%d",a);printf(":");if(b<10)printf("0%d",b);else printf("%d",b);printf(" PM\n");}}return 0;
}
D题题解
需要一点分析,首先二进制数有点多,100000 + ? ? ? ? ? ????? ?????
每个? 可以表示0或者1 那么有25 +1种
我们可以罗列出来,一个一个枚举。
这里所说的枚举其实可以更优雅一点,用DFS去搜索,看看给出的数字能不能凑出来
为什么DFS是可行的呢?
数字也就小于1e5级别,我们考虑最小的二进制数10 (1就不用说了,乘了也相当于没有乘)
1e4级别的数字顶多除4次10就要没了,所以说我们DFS深度肯定不会很多,四层足以,每次把当前数字能整除的,拿去除除看。
#include<bits/stdc++.h>
using namespace std;
int A[200]; //16
int len=0;
void dfs(int x){if(x>100000)return ;A[++len]=x;if(x%10==0)dfs(x+1);//只有偶数才能在末尾放1 dfs(x*10);//搜索构造二进制数
}
bool DFS(int x){if(x==1)return true;bool now=false;for(int i=1;i<=len;i++){if(x%A[i]==0){now=now | DFS(x/A[i]);}}return now;
}
int main(){int t;scanf("%d",&t);dfs(10);//搜索出可用的二进制数 while(t--){int n;scanf("%d",&n);bool ok=DFS(n);if(ok)printf("YES\n");else printf("NO\n");}return 0;
}
E题题解
题目所说的这种字符串,首先可以从长度分析,这种字符串的长度必定是S的某个因子
某则不可能复制回去。所以我们可以枚举长度。
这种子串从哪里枚举呢?你如果要复制回去的话,肯定要从头摆过去,所以说我们直接枚举S的一段前缀字符串,长度为S字符串的因子,然后带回去检验行不行。
注意还有一种可能,那就是枚举最末尾的那一段,因为它也算是最后被复制的那一段,我们可以利用它,来尝试往前面复制。
剩下的就看大家怎么写枚举了
[aaaa…bbbbb]
简单来说就是一方面你去枚举aaa能不能行
再枚举bbbb能不能行,两种方法取最小值
#include<bits/stdc++.h>
using namespace std;
char s[200005];
int main(){int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);scanf("%s",s+1);int ans=n;//初始值为N for(int i=1;i<=n/2;i++){//i 枚举子串长度if(n%i==0){int res=0;//有多少个不一样bool ok=true;for(int k=1;k<=n/i;k++){// 把S划分为N/i 段 每段都判断判断if(ok==false)break;for(int j=1;j<=i;j++){//这个j 对应的前缀 S[1~i] if(s[(k-1)*i+j]!=s[j])res++;//(k-1)*i表示前面已经枚举了多少段 算一个偏移量if(res>=2){ok=false;break;}}}if(ok){ans=i;break;}}}for(int i=1;i<=n/2;i++){if(n%i==0){int res=0;bool ok=true;for(int k=1;k<=n/i;k++){if(ok==false)break;//倒着枚举要注意,不是枚举后缀//而是枚举S[j~n] 从左到右能不能复制 for(int j=n-i+1,q=1;j<=n;j++,q++){if(s[(k-1)*i+q]!=s[j])res++;// j表示S[j~n]//S[(K-1)*i+Q]是枚举段 if(res>=2){ok=false;break;}}}if(ok){ans=min(ans,i);break;}}}printf("%d\n",ans);}return 0;
}




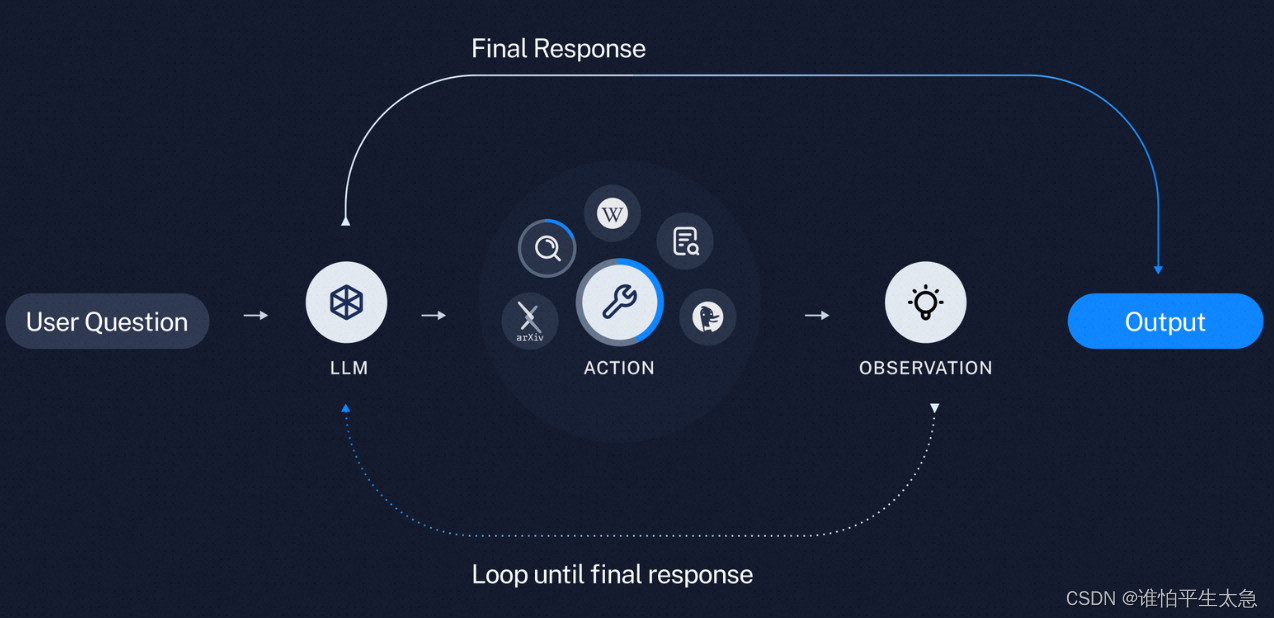
![[datawhale202405]从零手搓大模型实战:TinyAgent](https://img-blog.csdnimg.cn/direct/efa861cd0ff240b2bc3a421e97300d86.png)