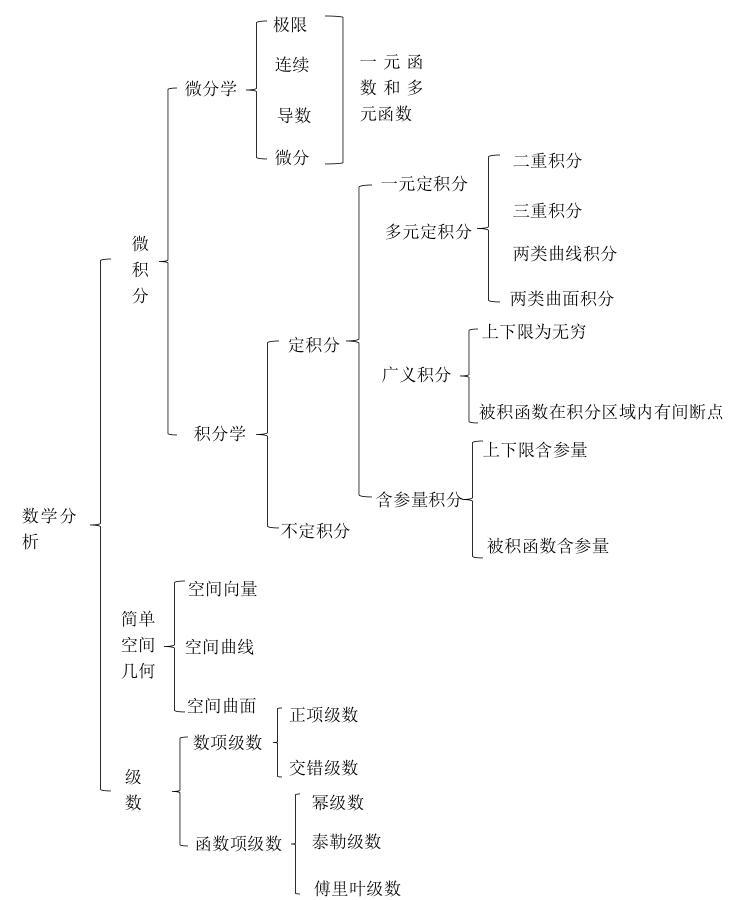
一、总览

• 微分学
• 积分学
• 级数论

二、微分学

1. 极限和连续

相关知识：数列的极限、收敛数列之性质、函数极限、函数极限性质、无穷大无穷小、等价无穷下、洛必达法则、函数的连续和间断、极限的求法。

2. 一元/多元函数微分学

相关知识：导数，可微，极值点和驻点、判断极值点的条件、凹凸性的定义、凹凸性的充分条件、凹凸性的充要条件、渐近线的定义。偏导数、可微、偏导数连续性、多元函数微分法则、隐函数定理、多元函数的极值和最值。

3. 微分定理

3.1 中值定理（mean value theorem）

一段连续光滑曲线中必然有一点，它的斜率与整段曲线平均斜率相同（严格的数学表达参见下文）。中值定理又称为微分学基本定理，拉格朗日定理，拉格朗日中值定理，以及有限改变量定理等。

如果函数 f(x) 满足在闭区间[a,b]上连续；在开区间(a,b）内可导，那么在（a,b）内至少有一点 ε (a<ε<b)，使等式成立。

3.2 柯西中值定理

若函数ƒ(x)与g(x)在闭区间【α,b】上连续，在开区间(α,b)内可微,则在这个区间内至少存在一点ξ，使得当g(x)=x时，上面定理与拉格朗日定理有同一形式，所以柯西中值定理是拉格朗日定理的最一般的形式。

三、积分学

1. 积分定理

1.1 积分第一中值定理

积分中值定理揭示了一种将积分化为函数值， 或者是将复杂函数的积分化为简单函数的积分的方法。积分第一中值定理：

1.2 积分第二中值定理

积分第二中值定理是与积分第一中值定理相互独立的一个定理，属于积分中值定理。它可以用来证明Dirichlet-Abel反常、Riemann积分判别法。

设f(x)在[a,b]上可积，g(x)在[a,b]上单调，则存在ξ∈[a,b]，使得

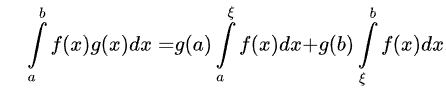
1.3 牛顿-莱布尼茨公式（Newton-Leibniz formula）

通常也被称为微积分基本定理，揭示了定积分与被积函数的原函数或者不定积分之间的联系

如果函数 f(x) 在区间 [a,b] 上连续，并且存在原函数 F(x), 则：

四、级数论

1. 无穷级数

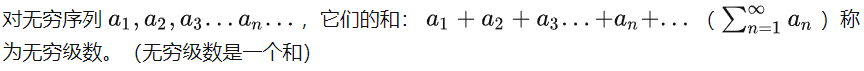
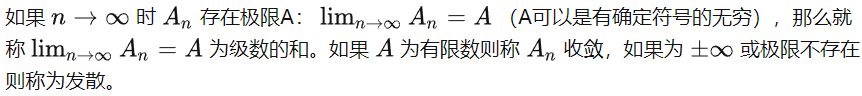2. 正项级数

2.1 正向级数收敛条件

有上界则收敛，否则发散

如果级数收敛，则其任何一个余式也收敛（修改级数前面有限个项，不影响级数的收敛或发散）

2.2 比较定理（只适用于正项级数）

 

2.3 基于比较定理的判别法

• 柯西判别法： 做序列  ，将其极限与1比较
• 达朗贝尔判别法：做序列 , 其极限小于1则收敛，大于1则发散（与柯西判别法原理相同）

References

微分积分简要总结 - 简书

级数总结 - 知乎