文章目录
- 1. 导数求解
- 1.1 显函数求导
- 1.2 隐函数求导
- 2. 极限求解
- 2.1 单变量极限
- 2.2 多变量极限
- 3. 积分求解
- 3.1 不定积分
- 3.2 定积分计算
- 3.2.1 解析解
- 3.2.2 数值解
- 4. 级数展开求和
- 4.1 泰勒级数展开
- 4.2 级数求和
- 5. 求解微分方程
- 5.1 符号解
- 5.2 数值解
1. 导数求解
1.1 显函数求导
MATLAB 求解导数一般使用 diff 函数,其一般由一下四种调用格式:
格式一
diff(s)
其中 s是符号表达式,系统按照 findsym 函数指示的默认变量求一阶导。
格式二
diff(s, v)
以 v 为变量, 对符号表达式 s 求一阶导。
格式三
diff(s, n)
其中 s是符号表达式,系统按照 findsym 函数指示的默认变量求 n 阶导。
格式四
diff(s, v, n)
以 v 为变量, 对符号表达式 s 求 n 阶导。
例
y = − x s i n ( x ) y=-xsin(x) y=−xsin(x),求 y ′ , y ′ ′ y',y'' y′,y′′。
syms x;
y = -x * sin(x);
dy = diff(y,x);
d2y = diff(y,x,2);
输出答案:
dy =
- sin(x) - x*cos(x)
d2y =
x*sin(x) - 2*cos(x)
1.2 隐函数求导
已知隐函数的数学表达式为 f ( x 1 , x 2 , ⋯ , x n ) = 0 f(x_1, x_2, \cdots ,x_n)=0 f(x1,x2,⋯,xn)=0,若想要求出 ∂ x i ∂ x j \frac{\partial x_i}{\partial x_j} ∂xj∂xi,可以使用下面的公式 ∂ x i ∂ x j = − ∂ ∂ x j f ( x 1 , x 2 , ⋯ , x n ) ∂ ∂ x i f ( x 1 , x 2 , ⋯ , x n ) \frac{\partial x_i}{\partial x_j}=- \frac{\frac{\partial}{\partial x_j}f(x_1, x_2,\cdots,x_n)}{\frac{\partial}{\partial x_i}f(x_1, x_2,\cdots,x_n)} ∂xj∂xi=−∂xi∂f(x1,x2,⋯,xn)∂xj∂f(x1,x2,⋯,xn)
例
z = f ( x , y ) z=f(x,y) z=f(x,y) 由 x 2 − y 2 + 2 z 2 = a 2 x^2-y^2+2z^2=a^2 x2−y2+2z2=a2 定义,求 z x ′ , z y ′ z_x',z_y' zx′,zy′。
syms x y z a;
f = x^2 - y^2 + 2 * z^2 - a^2;
zx = -diff(f,x)/diff(f,z)
zy = -diff(f,y) / diff(f,z)
输出答案:
zx =
-x/(2*z)
zy =
y/(2*z)
2. 极限求解
极限的求解使用的是MATLAB中的 limit 函数,其调用一般有以下几种形式:
格式一
limit(f,x,a)
求解的问题形式是 lim x → a f ( x ) \lim_{x \to a} f(x) x→alimf(x)
格式二
limit(f,x,a, 'right')
求解的问题形式是 lim x → a + f ( x ) \lim_{x \to a^+} f(x) x→a+limf(x)
格式三
limit(f,x,a, 'left')
求解的问题形式是 lim x → a − f ( x ) \lim_{x \to a^-} f(x) x→a−limf(x)
2.1 单变量极限
例
求解下列极限 lim x → ∞ x ( 1 − 2 a x ) x s i n 3 b x , lim x → y − x n + y n x + y \lim_{x \to \infty}x(1-\frac{2a}{x})^xsin\frac{3b}{x},\lim_{x \to y^-}\frac{\sqrt[n]{x}+\sqrt[n]{y}}{x + y} x→∞limx(1−x2a)xsinx3b,x→y−limx+ynx+ny
syms x y a b n
f1 = x * (1 - 2 * a / x)^x * sin(3 * b / x);
f2 = (x^(1 / n) + y^(1 / n))/ (x + y);
limit1 = limit(f1, x, inf)
limit2 = limit(f2, x, y, 'left')
输出答案为
limit1 =
3*b*exp(-2*a)
limt2 =
y^(1/n - 1)
2.2 多变量极限
多变量极限同样可以运用 limit 函数进行求解,可以运用 limit 函数嵌套调用来求解。
例
求解下列极限 lim x → 1 y , y → y 0 e − 1 y 2 − x 2 \lim_{x \to \frac{1}{\sqrt{y}},y \to y_0}e^{-\frac{1}{y^2-x^2}} x→y1,y→y0lime−y2−x21
syms x y a;
f = exp(-1 / (y^2 - x^2));
L = limit(limit(f, x , 1 / sqrt(y)), y, inf)
输出答案为
L =
1
3. 积分求解
3.1 不定积分
不定积分的求解上MATLAB提供了 int 函数来进行求解,其调用形式如下:
F = int(fun, x)
含义为求解符号表达式 fun 中的变量 x 的不定积分。单变量情况下 x 可以省略。
另外,该函数求解的结果 F ( x ) F(x) F(x) 是积分原函数,实际的不定积分应该是 F ( x ) + C F(x) + C F(x)+C 构成的函数族,其中 C C C 为任意常数。
而且对于不可积的不定积分,MATLAB也是无能为力的。
例
求不定积分 ∫ x t 1 − x 2 d t \int \frac{xt}{1-x^2}dt ∫1−x2xtdt
syms x t;
f = x * t / (1 - x^2);
f1 = int(f, t)
答案为
f1 =
-(t^2*x)/(2*(x^2 - 1))
3.2 定积分计算
3.2.1 解析解
该种形式的定积分仍然可以使用 int 函数来进行求解,格式为:
I = int(f, x, a, b)
其含义为求解符号表达式 f 中自变量 x 在区间 (a,b) 的定积分。
例1
求定积分 ∫ 3 5 x 4 ( x + 1 ) 12 d x \int^{5}_{3} \frac{x^4}{(x + 1)^{12}}dx ∫35(x+1)12x4dx
syms x;
f = x^4 / (x + 1)^12;
answer = int(f, x, 3, 5);
答案为
answer =
171682309/57211644542976
例2
求二重积分 ∬ e − t x d t d x \iint e^{-tx}dtdx ∬e−txdtdx
syms t x c1 c2;
y = int(int(exp(-t * x), t)+c1,x)+c2
答案为
y =
c2 - ei(-t*x) + c1*x
3.2.2 数值解
对于不能求出解析解的定积分来说,int 函数是行不通的,这种时候就需要用到数值积分来进行求解定积分的近似值了,接下来我以 ∫ 0 1 x − 1 l n x ∗ ( 1 + x ) 2 \int_0^1 \frac{x - 1}{lnx * (1+x)^2} ∫01lnx∗(1+x)2x−1 为例介绍几种常用的数值积分方法。
- integral
该函数的调用格式如下所示:
integral(fun,xmin,xmax)
传入一个函数句柄 fun,求其在(xmin,xmax) 范围的定积分。
求解示例定积分方法为:
syms x;
y = @(x) (x - 1) ./ (log(x) .* (1 + x).^2); %传入的句柄是匿名函数
a = integral(y,0,1)
答案输出为:
a =
0.3046
值得一提的是,该处也能使用我上篇文章中讲解符号表达式中的精度控制来控制有效数字位数,且乘除法必须使用点乘与点除。
- trapz
该函数的调用格式如下所示:
trapz(x, y)
trapz 函数运用的是梯形法对定积分进行求解,传入x 与其对应的 y 值,就能自动计算出数值。需要注意的是,由于使用的是梯形法,所以传入的x 值中不能有无穷大点或定义不存在的点,否则返回的数值为 NAN 。
求解示例定积分方法为:
x = [0 : 0.0001 :1];
x = x(2: 10000); %去掉首尾两点
y = (x - 1) ./ (log(x) .* (1 + x).^2);
a = trapz(x, y)
上述代码中因为 x=0 和 x=1 的点在 y 中都没有意义,所以将首尾两个点去掉。
答案输出为:
a =
0.3046
- quad
quad函数家族中精度最高的当属quadgk函数,该函数使用的是自适应高斯-勒让德积分法来对定积分进行数值求解,其调用格式如下:
quadgk(fun , xmin, xmax)
用法与 integral 函数类似。
求解示例定积分方法为:
syms x;
y = @(x) (x - 1) ./ (log(x) .* (1 + x).^2);
a = quadgk(y, 0, 1)
答案输出为:
a =
0.3046
- integral2
计算二重积分时选择的函数为integral2,其调用格式如下:
integral2(fun,xmin,xmax,ymin,ymax)
含义为求解函数句柄 fun 在 (xmin, xmax) 以及 (ymin, ymax) 的定积分数值解。
例
求解下列二重积分的数值解: f ( x , y ) = 1 x + y ( 1 + x + y ) 2 , 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 − x . f(x,y)= \frac{1}{ \sqrt{x+y}(1 + x + y)^2},0 \leq x \leq 1,0 \leq y \leq 1-x. f(x,y)=x+y(1+x+y)21,0≤x≤1,0≤y≤1−x.
syms x y;
fun = @(x,y) 1./( sqrt(x + y) .* (1 + x + y).^2 );
ymax = @(x) 1 - x;
q = integral2(fun,0,1,0,ymax)
答案输出为:
q =
0.2854
三重积分使用 integral3 函数就行,在这里就不再赘述了。
4. 级数展开求和
4.1 泰勒级数展开
泰勒级数的展开可以使用函数 taylor 得到答案,其调用格式为:
格式一
taylor(f, x, k)
在 x = 0 x=0 x=0 这点对符号表达式 f 进行 T a y l o r Taylor Taylor 级数的 k 次展开,k 默认为 6。
格式二
taylor(f, x, k, a)
在 x = a x=a x=a 这点对符号表达式 f 进行 T a y l o r Taylor Taylor 级数的 k 次展开。
例
求 x + x 3 − x + x 2 3 \sqrt{x + x^3} - \sqrt[3]{x + x^2} x+x3−3x+x2 的3阶泰勒展开式。
syms x;
f = sqrt(x + x^3) - (x + x^2)^(1 / 3);
f1 = taylor(f, x, 3)
答案为
f1 =
30^(1/2) - 12^(1/3) - (x - 3)*((7*12^(1/3))/36 - (7*30^(1/2))/15) + (x - 3)^2*((13*12^(1/3))/1296 + (37*30^(1/2))/900) - (x - 3)^3*((203*12^(1/3))/139968 + (17*30^(1/2))/6750) + (x - 3)^4*((719*12^(1/3))/2519424 + (107*30^(1/2))/324000) - (x - 3)^5*((5957*12^(1/3))/90699264 + (1229*30^(1/2))/24300000)
复杂地莫名其妙的一串,手动求怕是得累死吧。
4.2 级数求和
级数求和使用的函数为 symsum ,其调用格式为:
symsum(f, k , k0, kn)
含义为对符号表达式 f 的变量 k ,求其从第 k0 项开始到第 kn 项的和。
例
求级数和 s 1 = 1 + 1 4 + 1 9 + ⋯ + 1 n 2 + ⋯ s_1=1 + \frac{1}{4} + \frac{1}{9}+ \cdots + \frac{1}{n^2} + \cdots s1=1+41+91+⋯+n21+⋯
syms n
s1 = symsum(1 / n^2, n ,1, inf)
答案为
s1 =
pi^2/6
5. 求解微分方程
5.1 符号解
用Matlab求解常微分方程的符号解,首先定义符号变量,然后调用命令 dsolve 。dsolve 的调用格式如下:
dsolve(eqns, conds)
式中:eqns为符号微分方程或符号微分方程组, conds 为初值条件或边值条件。
例1
试求微分方程 y ′ ′ ′ − y ′ ′ = x , y ( 1 ) = 8 , y ′ ( 1 ) = 7 , y ′ ′ ( 2 ) = 4 y'''-y''=x,y(1)=8, y'(1) = 7, y''(2)=4 y′′′−y′′=x,y(1)=8,y′(1)=7,y′′(2)=4
syms y(x);
dy = diff(y);d2y = diff(y,2); %定义一阶、二阶导数,用于初值条件赋值
y = dsolve(diff(y,3) - diff(y,2) == x, y(1)==8, dy(1) == 7, d2y(2) == 4);
y = simplify(y) %化简
注意,调用dsolve时里面的等于符号一定要是 ==。
输出为
y =
(17*x)/2 + 7*exp(x - 2) - 7*x*exp(-1) - x^2/2 - x^3/6 + 1/6
例2
试求常微分方程组 { f ′ ′ + 3 g = s i n x g ′ + f ′ = c o s x \begin{cases} f''+3g=sinx\\ g'+f'=cosx \end{cases} {f′′+3g=sinxg′+f′=cosx的通解和在初边值条件为 f ′ ( 2 ) = 0 , f ( 3 ) = 3 , g ( 5 ) = 1 f'(2)=0,f(3)=3,g(5)=1 f′(2)=0,f(3)=3,g(5)=1 的解。
syms f(x) g(x)
df = diff( f); %定义f的一阶导数,用于初值或边值条件的赋值
[f1, g1] = dsolve( diff(f,2) +3 * g == sin(x) , diff(g)+df ==cos(x)) %求通解
f1 = simplify(f1),gl = simplify(g1)% 对符号解进行化简
[f2, g2] =dsolve(diff(f,2) +3 * g ==sin( x) ,diff( g) + df ==cos(x) ,df(2 ) ==0,f( 3 ) ==3,g(5)==1)
f2 = simplify( f2), g2 = simplify( g2)%对符号解进行化简
输出为
f1 =
C1 + sin(x)/2 + (3^(1/2)*C2*exp(3^(1/2)*x))/3 - (3^(1/2)*C3*exp(-3^(1/2)*x))/3
g1 =
sin(x)/2 - (3^(1/2)*C2*exp(3^(1/2)*x))/3 + (3^(1/2)*C3*exp(-3^(1/2)*x))/3
f2 和 g2 太长了我就不打啦hhh。
5.2 数值解
很多的常微分方程都是没有符号解的,这种情况 dslove 函数是没有作用的,只有采用数值解来解出一个较为准确的近似值。
微分方程的数值解采用的是 ode45 和 ode15s 两个函数, ode45 求解的是非刚性微分方程, ode15s 求解的是刚性微分方程,刚性非刚性估计你们也不是很想懂,总之首先使用 ode45 求解就行,若求解失败或很慢, 换 ode15s 。
- ode45
该函数的调用格式如下所示:
[t,y] = ode45(odefun,tspan,y0)
其中 odefun 是函数句柄, tspan 是求解的区间, y0 是求解的初值列向量, 时刻 t 即求解对应的 x 坐标,与 y 是一一对应的。
例
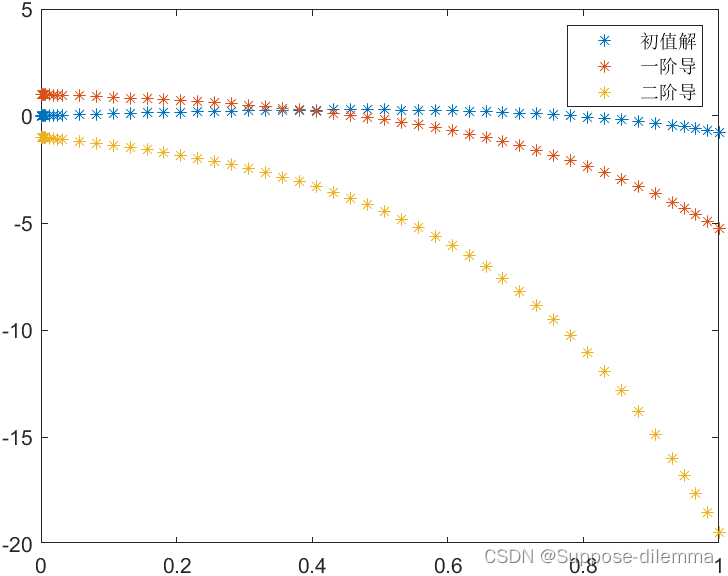
求解初值问题 y ′ ′ ′ − 3 y ′ ′ − y ′ y = 0 , y ( 0 ) = 0 , y ′ ( 0 ) = 1 , y ′ ′ ( 0 ) = − 1 y'''-3y''-y'y=0,y(0)=0,y'(0)=1,y''(0)=-1 y′′′−3y′′−y′y=0,y(0)=0,y′(0)=1,y′′(0)=−1
设 y 1 = y , y 2 = y ′ , y 3 = y ′ ′ y_1=y,y_2=y',y_3=y'' y1=y,y2=y′,y3=y′′,使用 ode45 函数首先要将方程变形,变为等式左边只有一个未知数的形式,如下:
{ y 1 ′ = y 2 y 2 ′ = y 3 y 3 ′ = 3 y ′ ′ + y ′ y \begin{cases} y_1'=y_2 \\ y_2'=y_3 \\ y_3'=3y''+y'y \end{cases} ⎩ ⎨ ⎧y1′=y2y2′=y3y3′=3y′′+y′y
其中 y 1 ( 0 ) = 0 , y 2 ( 0 ) = 1 , y 3 ( 0 ) = − 1 y_1(0)=0,y_2(0)=1,y_3(0)=-1 y1(0)=0,y2(0)=1,y3(0)=−1 。
ode45 函数的函数句柄必须接受两个参数 t,y ,参数 t 可以没有,但必须写上。
创建一个F.m 名字的文件,在里面写上函数的句柄,如下:
function dy = F(t,y)
dy = [y(2);y(3);3 * y(3) + y(2) * y(1)];
end
在命令行中进行求解,语句为:
[t, y] = ode45('F', [0 1], [0;1;-1]); %传入求解范围和初值条件
当然也可以使用匿名函数一行代码即可求解:
[t, y] = ode45(@(t,y) [y(2);y(3);3 * y(3) + y(2) * y(1)], [0 1], [0;1;-1])
其中求解的y(:,1)是初值问题的解, y(:,2)是解的导数, y(:,3) 是解的二阶导数。
使用下面语句可以将得到的点画出来:
plot(t, y, '*');
legend('初值解','一阶导', '二阶导');
画出的图像为:
在这里插入图片描述
- ode15s
ode15s函数与ode45函数的调用方法一致,调用的参数以及返回的参数形式也一致,只需要改个函数名就行,不同的是ode15s针对的是刚性微分方程。