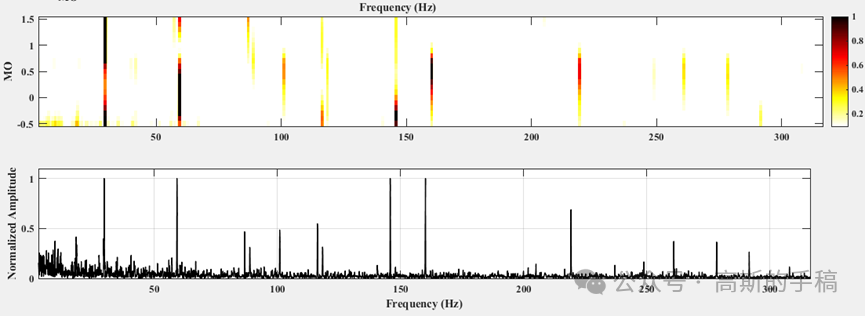
在众多的旋转机械故障诊断方法中,包络分析,又称为共振解调技术,是目前应用最为成功的方法之一。首先,对激励引起的共振频带进行带通滤波,然后对滤波信号进行包络谱分析,通过识别包络谱中的故障相关的特征频率,从而判断是否发生故障与故障的类型。然而,包络分析方法的主要难点在于共振频带的选取。为了解决这一难题,基于谱峭度的峭度图方法被提出,通过计算由STFT或者有限脉冲滤波器得到的窄带包络信号的峭度,确定信号中非高斯成分所在的频带。随着研究的深入,峭度图的缺点逐渐暴露。峭度指标不能区分冲击是否由循环冲击引起,因此,在两种情况下容易失效。第一种是存在较强的脉冲噪声时,第二种是故障脉冲重复频率较高时。
为了解决这一问题,众多学者提出了一系列的改进方法,例如:improvedKurto⁃gram,enhancedKurtogram,Protrugram,Info⁃gram,Autogram均取得了不错的效果。一些基于周期指标的峭度图被提出来,可以用来寻找具有指定周期成分所在的频带,极大地降低了背景噪声的影响。但是这类方法需要预知精确的故障周期,缺乏自适应性。到目前为止,找到最佳的解调频带依然不是一个简单的任务。峭度图方法寻找到的频带仅能识别一个最佳频带,由于缺陷产生的冲击会在不同的频率范围内激发机器结构产生共振,仅从一个频带恢复原信号,会丢失很多故障信息。尤其当信号中存在多个故障时,弱故障往往不能被识别,因此,需要对信号进行多频段滤波,才能完全提取出缺陷信号。
鉴于此,有大佬提出了一种新的非线性滤波的方法去分离信号,首先对振动信号进行傅里叶变换获得频域幅值谱和相位谱,通过对其幅值谱赋予不同权重的指数,并结合原始信号相位谱进行逆傅里叶变换,从而获得一系列的修正信号,最后通过修正信号平方包络的功率谱识别故障特征。该方法计算简单、效率高、自适应强,且摆脱了对评价指标的依赖,取得了显著的效果。
function Ren=renyi_entropy(TFR,t,f,alpha)
% Ren=renyi_entropy(TFR,t,f,alpha) calculates Renyi entropy from 2-D TFR
%
% Inputs:
% TFR : (M,N) 2-D TFR function.
% T : a time vector (default : (1:N)).
% F : a frequency vector (default : (1:M)).
% ALPHA : Renyi measure order (default : 3).
%
% Outputs:
% Ren=1/(1-ALPHA)*log2[Sum[TFR(Fi,Ti)^ALPHA dFi.dTi]]
% Fi,Ti : Alpha-order Renyi entropy
% ALPHA = 1: limit case, the outcomes will be Shannon entropy
% Sha = - Sum[TFR(Fi,Ti)log2[TFR(Fi,Ti)]dFi.dTi]
% Fi,Tiif (nargin == 0),error('At least one parameter required');
end;[M,N] = size(TFR);
if (nargin == 1),t=1:N; f=(1:M)'; alpha=3;
elseif (nargin == 2),f=(1:M)'; alpha=3;
elseif (nargin == 3),alpha=3;
end;f=sort(f); %sort frequency vector in ascending order such that the first
%row TFR must correspond to the lower frequenciesTFR = TFR./trapz(f,trapz(t,TFR,2));
% Normalisation TFR;
%trapz function is used to calculate 2D integral of %matrix TFR according
%to abscissa X and ordinate Yif alpha == 1 % limit case case: Shannon entropyif (min(min(TFR))<0)error('distribution with negative values => alpha=1 not allowed');elseRen=-trapz(f,trapz(t,TFR.*log2(TFR+eps),2));end
else % Renyi entropyRen=1/(1-alpha)*log2(trapz(f,trapz(t,TFR.^alpha,2))+eps);完整代码:https://mbd.pub/o/bread/mbd-ZJeYmJdv
end