交错字符串

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空
子字符串

子字符串 是字符串中连续的 非空 字符序列。

• s = s1 + s2 + … + sn
• t = t1 + t2 + … + tm
• |n - m| <= 1
• 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

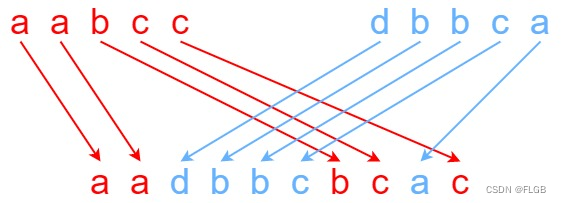
输入：s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出：true

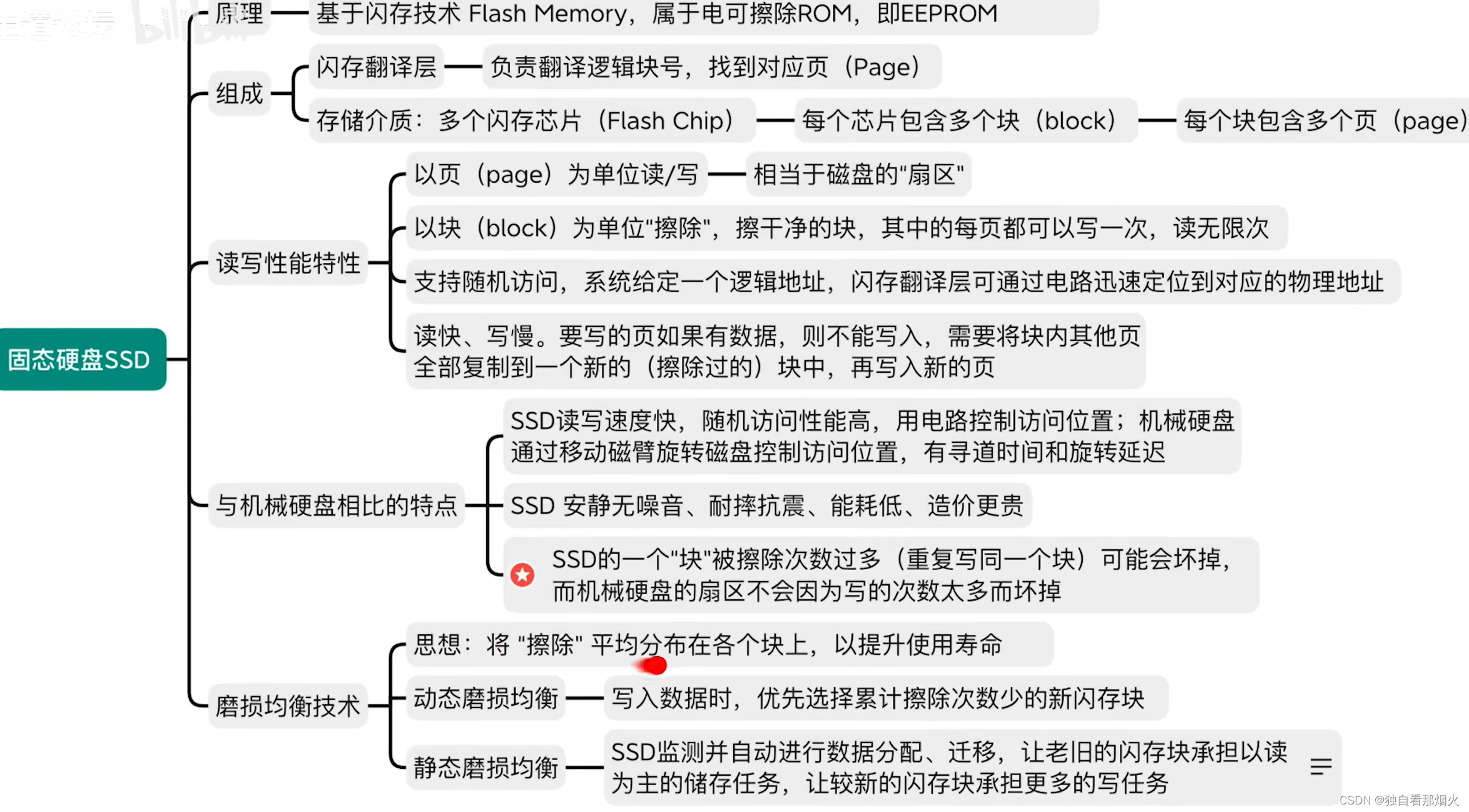
解题思路

定义一个二维布尔数组 dp，其中 dp[i][j] 表示 s3 的前 i + j 个字符是否可以由s1 的前 i 个字符和 s2 的前 j 个字符交错组成。具体的递推关系如下：

初始条件：

• dp[0][0] = true，表示两个空字符串可以组成空字符串。

递推关系：

• 如果 dp[i-1][j] 为真且 s1[i-1] == s3[i + j - 1]，则 dp[i][j] = true。
  dp[i-1][j] 表示 s3 的前 i + j - 1 个字符可以通过 s1 的前 i-1 个字符和 s2 的前 j 个字符交错组成。
  如果 s1 的第 i 个字符 s1[i-1] 等于 s3 的第 i + j 个字符 s3[i + j - 1]，
  则可以在 s3 的前 i + j - 1 个字符的基础上加上 s1 的第 i 个字符组成 s3 的前 i + j 个字符。
  因此，dp[i][j] = true。

• 同理，如果 dp[i][j-1] 为真且 s2[j-1] == s3[i + j - 1]，则 dp[i][j] = true。

最终结果：

• dp[s1.length()][s2.length()] 表示 s3 是否可以由 s1 和 s2 交错组成。

Java实现

public class InterleavingString {public boolean isInterleave(String s1, String s2, String s3) {int m = s1.length();int n = s2.length();if (m + n != s3.length()) {return false;}boolean[][] dp = new boolean[m + 1][n + 1];dp[0][0] = true;// 初始化第一列for (int i = 1; i <= m; i++) {dp[i][0] = dp[i-1][0] && s1.charAt(i-1) == s3.charAt(i-1);}// 初始化第一行for (int j = 1; j <= n; j++) {dp[0][j] = dp[0][j-1] && s2.charAt(j-1) == s3.charAt(j-1);}// 填充 dp 表for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = (dp[i-1][j] && s1.charAt(i-1) == s3.charAt(i + j - 1)) || (dp[i][j-1] && s2.charAt(j-1) == s3.charAt(i + j - 1));}}return dp[m][n];}// 测试用例public static void main(String[] args) {InterleavingString solution = new InterleavingString();System.out.println(solution.isInterleave("aabcc", "dbbca", "aadbbcbcac"));  // 期望输出: trueSystem.out.println(solution.isInterleave("aabcc", "dbbca", "aadbbbaccc"));  // 期望输出: false}
}

时间空间复杂度

• 时间复杂度：O(m * n)，其中 m 是 s1 的长度，n 是 s2 的长度，需要遍历整个 dp 数组。
• 空间复杂度：O(m * n)，需要一个二维数组 dp 存储中间结果。