生产网络与股票回报:垂直创造性破坏的作用

本文从实证和理论两方面研究了生产网络中企业风险与企业与消费者距离之间的关系。我们记录了两个新事实:离消费者越远的企业，其风险溢价越高，对总生产率的影响也越大。我们用一个具有多层生产过程的一般均衡模型来定量地解释这些发现。经济力量是“垂直创造性破坏”，也就是说，对供应商的积极生产力冲击使客户的现有资产贬值，从而降低了下游企业价值的周期性。我们表明，纵向创造性破坏随竞争和企业特征而变化，并在风险溢价方面产生相当大的横断面差异。

生产发生在一个由长而交织的供应链组成的复杂网络中，在这个网络中，最终消费品的生产经过多个中间阶段。这种从最上游的公司开始，到最下游的公司结束的多级生产过程，反映了生产的垂直组织。尽管它与经济活动相关，但很少有人知道生产的这一垂直维度与资产价格的关系，尤其是在公司层面的粒度上。企业对宏观经济风险的暴露如何随上游而变化?企业的上游性与预期收益之间有什么关系?供应链特征，如竞争强度，是否影响企业的资本成本?在本文中，我们试图从实证和理论两方面解决这些问题。

直观地说，并非所有生产链上的企业都能从技术进步中获得同等的利益。改进供应商新资本生产的创新可以使客户的现有资本贬值。这使得不同的风险暴露沿着生产力冲击的链被证实。这些风险暴露也受到供应商面临的竞争的影响，因为垄断力量配给新资本的生产。我们在本文中发展了这种直觉，并在经验上证实了它。

解决上述问题的主要经验挑战是全面的数据的可用性，允许测量公司在网络中的颗粒位置随着时间的推移。为了克服这一挑战，我们使用了一个新颖的供应商-客户关系数据库，它允许动态计算公司的上游。为了计算企业的上游度量，我们将一个生产网络分解为多个生产层。第j层的所有企业都被从生产最终消费品的底层的j条供应商-客户链(沿着最短的链)分开。公司的垂直位置与它所属的层相对应。

我们的第一个贡献是实证地记录了两个新颖的风格化事实，它们突出了企业在网络中的垂直位置与其风险之间的单调关系。首先，我们证明了一个公司离最终消费者越远(即其垂直位置越高)，其平均股票回报就越高。以距离消费者最远的公司做多，距离最短的公司做空的投资策略，每月产生105个基点的回报。我们将这种价差称为TMB。其次，我们证明了企业对总生产率的暴露随其垂直位置单调增加。

我们的第二个贡献是提出并检验一个共同解释这些事实的定量理论。我们的解释是基于多层供应链经济中出现的一种新的创造性破坏形式。我们建立了一个具有多层生产的一般均衡模型。每一层的输出都卖给它的下一层，下一层用输入产生自己的输出。底层，零层，生产最终消费品。

正向的总生产率冲击对企业估值具有双重影响。一方面，它对每个层的产出起到了积极的需求冲击作用，这意味着更高的未来现金流和改善的增长选择。这种使所有公司估值增值的需求效应也存在于单一部门设置中。然而，一个单独的影响存在，这是我们的多层环境的新。同样的正冲击增加了公司的直接和间接供应商的生产力。当他们都变得更有效率时，公司投入的供给曲线向右移动。这种供给效应对公司的现有资产(已安装资本或库存)的估值造成了下行压力。技术进步使企业资本投入的生产成本更低。在竞争环境下，这会侵蚀企业的边际价值安装资本。我们把这种供给效应称为垂直创造性破坏。

供给效应的强度在各层之间是不均匀的。底层企业受供给效应的影响最大。它现有的资本是用它上面所有层所生产的商品建立起来的。当每一种中间资本产品的生产成本变得更低时，供给效应就会逐渐向下延伸，而底层的资产就地价值面临着最大的下行压力，因为它的重置成本变得相对最便宜。相比之下，顶层公司不受垂直创造性破坏力的影响，因为它没有供应商。中层企业经历了一定程度的这种累积供应效应，但没有底层企业那么强烈，因为它们的间接供应商较少。由于负供给效应部分抵消了正需求效应，垂直创造性破坏通过使企业的生产率暴露不为正起到对冲作用。这一逻辑既解释了TMB的分布，也解释了为什么生产力beta随垂直位置单调增加。

我们使用一个简化模型以封闭形式将这种直觉形式化，并在一个校准的全DSGE模型中检验其量化能力。校正后的模型在股票回报、生产率风险敞口和垂直位置之间产生单调关系，并且TMB年差为12%，接近其实证对应。

为了加强模型和数据之间的联系，我们对机制执行了几次测试。首先，该模型预测托宾q、投入价格和投资率对顶层公司更具周期性。我们使用Compustat数据和BLS的中等需求价格指数来证实这一点。第二，具有垄断权力的增强模型预测，当企业拥有更大的垄断权力时，TMB价差更小。

当生产率提高，垄断供应商并不像竞争供应商那样增加供应量。因此，对客户现有资产的创造性破坏减少了。与这一预测一致的是，对于数据中竞争较低的企业的子样本，TMB较小。增广模型的逻辑也有一个新颖的含义。它预测了企业的资本成本与其上游供应商的竞争力之间存在负相关关系。我们一致地发现，消费品生产商的直接或间接供应商有更多的竞争对手获得更高的预期回报。第三，我们证实了模型的预测，即对实体资产依赖度较高的企业:价值型企业、资本折旧率较低的企业、组织资本较低的企业和库存较多的企业，TMB利差更大。对于这些公司来说，更大一部分的公司价值来自于现有资产，这是受垂直创造性破坏的组成部分。

我们证实了我们的经验发现的稳健性。当我们(a)使用美国经济分析局(BEA)的投入产出表来计算1973年至2017年的行业间TMB差值时，TMB仍然具有显著性;(b)使用Compustat Segment数据库构建一个1985年至2017年的样本，考虑每个供应商-客户关系的强度;(c)使用不同的再平衡或方法来计算垂直位置。

本文提供了三条文献线索:创造性破坏、生产网络和基于生产的资产定价。熊彼特的创造性破坏思想影响了许多领域的经济研究最近，它还刺激了金融领域的研究。一些论文利用并非所有公司从创新中获得同等收益的事实来推导截面风险溢价的含义。例如，Gârleanu, Kogan, and Panageas (2012)， Loualiche (2016)， Barrot, Loualiche, and Sauvagnat(2019)，以及Kogan, Papanikolaou, and Stoffman(2020)研究了替代风险，即创新使新公司受益，而牺牲现有公司。在这些论文中，创造性破坏是横向的:它是由公司的竞争对手诱导的。我们对这篇文献的贡献是介绍垂直创造性破坏:供应商的创新使客户公司贬值。我们的模型揭示了一个看似违反直觉的结果:这种创造性的破坏为客户公司提供了一种对冲，并降低了其资本成本。

我们的论文也与最近连接网络和资产价格的文献密切相关。Cohen和Frazzini(2008)以及Menzly和Ozbas(2010)通过供应商-客户链接研究了股票回报的可预测性。相比之下，我们研究了不同层的同时期横向回报影响。Ahern(2013)发现网络中心性越高的行业收益越高。我们验证了TMB传播不能用中心性来解释。Ozdagli和Weber(2018)发现货币冲击的传播具有相当大的网络效应。本文主要研究普通生产力冲击产生的网络效应。Herskovic(2018)根据网络集中度和稀疏度的变化推导出两个风险因素。相比之下，我们通过建模供应链来关注生产的垂直维度。我们发现TMB随着链长的增加而增加。这不是稀缺性或连通性的结果，而是更大的累积供应效应。

更广泛地说，我们的论文是关于将投资与资产价格联系起来的研究。我们模型的新颖之处在于考虑多层生产过程，而不是假设一个单一的部门。一些研究研究了资产定价对两部门经济的影响。戈麦斯、科根和Y ogo(2009)的研究表明，耐用品生产商的预期回报率高于非耐用品生产商。TMB扩散与这个结果无关。Yang (2013)， Papanikolaou (2011)， Garlappi and Song (2017a, 2017b)研究了消费部门和投资部门的溢价差异。我们背离了这些研究，采用了一种基于网络的上游衡量方法，这种方法比行业分类更细化。大部分TMB利差来自投资部门内部，而不是来自消费与投资公司的回报差异。

1 垂直位置的数据和测量

1.1数据

我们在实证分析中使用的主要数据库是CRSP股票数据库(用于股票回报)、Compustat北美数据库(用于会计数据)和FactSet Revere关系数据库(用于关于供应商、客户和竞争对手的信息)。

FactSet Revere数据库提供了目前可用的最全面的企业级供应商-客户关系覆盖。它包括供应商或客户(或双方)公开的关系，每个关系都有开始和结束日期。FactSet的分析师会定期监控这些关系数据。他们从公司的年度报告中收集信息，根据规定，年度报告应包括产生10%以上销售额的客户的姓名，以及来自其他来源的信息，包括新闻稿和公告、投资者陈述和公司的报告。全面的供应商-客户数据使我们能够衡量企业的上游地位。该数据库还提供了有关公司竞争对手的信息，这对我们的一些测试是有用的。

我们的样本周期是从2003年4月数据库启动的时候，到2013年9月从Revere购买它的时候。为了给分析师足够的时间来全面更新供应商-客户关系，我们只使用截至2012年12月的关系。在此期间，FactSet Revere数据库包括了193,851对公司之间的433,271个供应商-客户关系，覆盖了总计43,656家公司(其中许多是私营公司和国际公司)。我们通过删除重复的记录和冗余的关系(其开始和结束日期位于同一对公司之间更长的关系的时间段内)来清理它。如果两个连续关系之间的时间间隔不超过6个月，我们还可以将同一对公司在不同时期的多个关系合并为一个连续关系。在这些步骤之后，有206,264个供应商-客户关系。

我们将FactSet Revere数据库与Compustat North America和CRSP数据库合并(使用CUSIP和CRSP-Compustat链接表)。我们排除了金融公司(GICS代码40)、工业集团公司(GICS 201050，它们在生产网络中的垂直位置没有被精确测量)以及便士股(即上月价格低于1美元的股票)。我们匹配的样本共有5926只普通股(CRSP股票代码为10、11或12)。在样本期内，CRSP-Compustat合并数据库中非便士、非金融股和非集团普通股的总数为6,437。因此，我们的匹配样本包含了这些股票的大部分(92%)。

1.2垂直位置测量

我们现在描述我们对主要的基于生产的利益特征的度量:一个公司的垂直位置(即它的上游)。生产网络可以被划分为多个部分，在同一部分的公司与最终消费者之间的距离相似。我们把这些部分称为生产层。处于网络底层的企业生产最终的消费品。所有其他公司都是底层公司的直接或间接供应商。我们将任何企业的垂直位置定义为其与底层企业之间的供应商-客户联系的最小数量。第一层的公司至少向第0层的一家公司供货。第i层的公司至少向第i - 1层的公司提供服务，而在第i - 1层以下的公司则不提供服务。

我们计算垂直位置的方法是基于Gofman(2013)。形式上，考虑一个距离矩阵Dt有nt行和mt列，nt是t月网络中的公司总数，mt是t月消费品生产商的数量。该矩阵的一个元素Dt（i，j）测量公司i和消费品生产商j之间供应商-客户联系的最小数量。给定矩阵Dt，企业i的垂直位置定义为与任何消费品生产商的供应商-客户关系的最小数量。

 

垂直位置测量是一种全球性的测量方法，它依赖于整个网络结构。一个公司的垂直位置可以改变，即使它的直接供应商和客户不改变。每个月的生产层数是内生的，取决于观察到的供应商-客户关系。考虑到垂直位置公司可以随时间变化，我们以每月为基础计算垂直位置的度量，以反映最新的信息。

我们将上述方法应用于我们的revere - compustat匹配的样本。首先，我们为所有非必需消费品(GICS代码25)和必需消费品(GICS代码30)部门的公司分配一个垂直位置为0。其次，我们使用公式(1)来估计样本中剩余企业的垂直位置，使用所有的供应商-客户关系，其中任何一方都来自这个样本。我们要求一种关系至少持续6个月，然后用它来计算垂直位置。因此，从2003年9月开始，我们获得了一个全面的公司水平的垂直职位面板。据我们所知，我们的论文是第一篇对美国公司的大截面动态衡量上游的论文。

1. 程式化的事实:垂直位置，风险，和股票回报

我们根据垂直位置对公司进行分类，从而形成投资组合。为了确保投资者了解有关供应商-客户关系的公开信息，我们使用在第t - 2月底计算的垂直头寸在第t月初对公司进行排序(第7.2节在其他排序方案下显示了类似的结果)。因此，我们的投资组合持有期从2003年11月开始。生产层次的数量和企业在这些层次上的分布是内生的，因此企业不需要在不同层次上平均分配。事实上，正如我们在第8节详细讨论的，上层生产(垂直位置较高的层次)包括较少的公司。为了减少顶层公司数量较少所带来的噪音，我们将所有垂直位置在5个或以上的公司合并到一个单独的投资组合中，同时将低于5个层次的公司保留在单独的投资组合中。总之，我们获得了六个组合，代表六个生产层。

 

2.1程式化事实1:分层投资组合回报和TMB利差

表1展示了我们从分类投资组合中发现的第一个主要的典型事实:垂直位置和平均股票回报之间的单调关系，以及生产的顶层和底层之间的可观的回报差(TMB差)。从底层到顶层，价值加权和等加权平均收益都是单调递增的。当投资组合进行价值加权(等加权)时，TMB息差为每月105(108)个基点。两者在经济上和统计上都具有显著意义。表1还表明夏普比率随垂直位置而上升。价值加权(等加权)TMB投资组合的年化夏普比率为0.68(0.82)。而同期，市场组合的夏普比率为0.39,SMB因子为0.28,HML因子为0.29。

TMB扩散并不是FactSet Revere数据库特有的。第7节使用不太详细的BEA输入-输出表和Compustat Segment数据库来说明这种分布也存在于更长的样本周期中。在线附录章节OA.8也表明TMB价差在很大程度上独立于已知的与生产相关的和跨行业的价差，包括耐用品和非耐用品之间的价差，投资和消费公司之间的价差，以及账面市值溢价等。

2.2程序化事实2:分层投资组合暴露于生产率冲击

与上面报告的垂直位置和平均回报之间的单调关系相关，我们在这一节检验这种关系是否是基本宏观经济风险暴露的结果。我们建立了第二个程式化的事实:处于顶层的公司比处于底层的公司更容易受到总体生产力冲击的影响。

我们使用两个代理来代表总生产力。第一个是由美国劳工统计局(BLS)发布的季度劳动生产率数据。使用劳动生产率来衡量总生产率，因为它是基于容易观察到的变量，即附加值和工时，所以估计噪声较小。第二个指标是希克斯中性生产力冲击，我们称之为索洛剩余。这个代理是直接从旧金山联邦储备银行公布的TFP数据计算出来的(见Basu, Fernald，和Kimball 2006;Fernald 2014)。确保Hicks-neutral冲击相似理论分析,我们遵循Croce(2014),并调整TFP增长措施,占物理非住宅资本(设备和土地),和其他形式的资本不传播作为输入的供应链,如艺术或住宅capital.11构建的Solow残差与Fernald(2012)利用调整后的TFP之间的相关系数为0.97。

表2的面板A报告了每一层的回归系数(贝塔)和TMB投资组合相对于总生产率的回归系数(贝塔)，这些回归系数来自于对生产率衡量的年化增长的季度投资组合回报的预测。总的来说，生产力随着垂直位置的增加而增加。使用这两个生产力代理，底层的beta版大约是1.2，而顶层的beta版超过2.5。

预期收益和生产率之间的关系可能不是线性的。例如，如果每个层对总生产率的暴露是随时间变化的，就会出现这种情况。这就是在第3节中用来解释我们的发现的模型中的情况。因此，在表2的面板B中，我们更改了投影规范，以包含生产率的二次项。我们将线性项和二次项的斜率系数结合起来，形成生产率贝塔。具体地说:

 

为什么垂直位置较高的企业更容易受到总生产率的影响?在下一节中，我们提出一个DSGE模型来联合解释程式化事实1和2。挑战在于将各层的风险暴露模式从定性和定量两方面内源性地反映到总生产率中，以便与可观的TMB价差相匹配。

3.模型

经济中有N +1个生产层，用j∈{0,1，…，N}来表示。每个生产层都被一个单独的代表公司捕获，在完全竞争下运作。公司在{1，..，N}生产差异化的(中间)资本货物。一个在j层∈{1，..，N}向垂直于其下一层的企业提供资本，j−1。底层的企业(j = 0)生产最终消费品，卖给家庭消费。

3.1公司

在层j∈{0,1，…，N}从家庭中雇佣劳动力nj,t，并拥有资本kj,t，这是特定的。在受第j层生产率冲击Zj,t的影响下，企业使用固定收益来衡量资本和劳动力的柯布-道格拉斯生产函数的产出。

 

其中α为产出的资本份额。由于顶层(N层)没有资金提供者，故假定其资本存量随时间固定(kN,t =kN,0)。我们在在线附录章节OA.5.3中放宽了这个假设。j层中企业的资本∈{0，..，N−1}的折旧率为δ

 

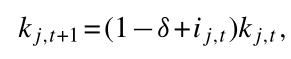
其中，ij,t表示企业j的投资率。第0层≥j≥N−1的企业，如果希望投资金额为ij,tkj,t，则必须直接从其上一层购买(ij,t)kj,t单位的层特定资本货物。购买j层资本货物是在j+1层的均衡产出价格Pj+1下进行的。

 

其中Wt表示每单位劳动力的实际工资。在顶层公司的资本固定的情况下，顶层公司的股利同样由dN,t =PN,tYN,t−WtnN,t给出。每个企业都选择最优投资(顶级企业除外)和最优招聘，以使其市场价值最大化，取给定的工资Wt，产出价格Pj,t,j∈{0，..，N}，和家庭Mt,t+1的随机折现因子。具体来说，layer-j代表企业最大化:

 

3.2家庭

经济由一个具有代表性的家庭组成。家庭从Epstein和Zin(1989)和Weil(1989)的效用中获得消费Ct流的效用：

其中β为主观折现因子，γ为风险规避系数，ψ为跨期替代弹性(IES)。为了便于记法，将参数θ定义为θ≡1−γ 1−1ψ。请注意，当θ =1时，即γ =1/ψ时，递归首选项坍塌为电力效用。当风险厌恶超过IES的倒数(γ >1/ψ)时，代理倾向于消费路径的不确定性的早期解决;否则，代理倾向于延迟解决不确定性。家庭向所有企业提供劳动力是没有弹性的。它的收入来自劳动，以及所有N +1企业的股息。在预算约束下，家庭选择分层特定的劳动力供给和消费以实现其终身效用最大化:

 

其中ωj t是家庭在第j曾公司的所有权中所占的份额，

是除息公司价值。随机折现因子(SDF)用于对各层的股利公司进行折现。

 

 

3.3均衡

在均衡条件下，工资Wt和产出价格{Pj,t}j∈{0，..，N}，将清空所有市场:

劳动力市场结算：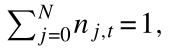

 

差异化资本品市场结算：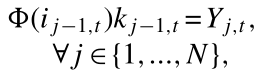

 

消费品市场结算：

 

企业所有权市场结算：

 

在线附录的第OA.5节讨论了我们的建模假设，包括沿供应链传输的货物的性质、跨层的预先异质性、线性网络结构和定时不变的垂直位置公司。我们证明了我们的结果对于沿着这些线进行的各种扩展是很强的。

4.封闭的定性结果

在第3节中概述的一般均衡模型(以后是全DSGE模型)不承认一个封闭形式的解，必须用数值方法求解。在本节中，我们制定了一个变化的全DSGE模型，是可处理的。本节的目的是将第5节中给出的经过校准的全DSGE模型定量结果背后的直观直观形式化。为了获得一个封闭解，我们做了一些简化假设:

假设1 没有调整成本 我们假设没有资本安装摩擦(即φ = 1)。

假设2 独立随机游动和标准随机游动 第j层生产力增长

 

假设1和2简化了设置，使其易于处理。假设所有的生产力冲击是正交的(ρz = 0)是为了经济机制的透明度。它可以隔离j层的创新对k层估值的影响。在完整的DSGE模型中，为了校准的简单性，ρz被设为1，我们将在本节后面引入这个假设(称为假设2)。

假设3 资本质量冲击 每个层的资本受到零平均质量冲击χj的影响，该冲击在t +1时间内实现。具体来说，式(4)中的资本积累动态被改变为

 

其中，Ij,t≡Ij, tkj,t为投资金额，χj,t是独立于时间的，Et[χj,t+1] = 0。假设3仅用于获得一个封闭形式的解。在标准RBC模型中，以及在全DSGE模型中，不存在资本质量冲击(χj,t+1 = 0)。经济中的生产力变化导致了过渡期(s)，因为经济将各层的资本调整到新的最优。这些转变使得一个封闭解不可行。质量冲击χj可以消除这些过渡时期，因为每个层的资本在t +1时间瞬间调整“正确的”数量，以恢复稳定状态。在我们的设置中，质量冲击χj可以立即恢复每个层j的稳定状态，只要假设。该假设意味着企业的问题在潜在的生产力冲击中是同质的，这简化了解决方案(例如，Gabaix(2011)和Gourio (2012)，

 

假设4 折旧率不满:δ <1。

假设4保证公司在t时期的一部分固定资本存量在下一个时期t +1保持正值。因此，股本的影子价格可以用来为(除息)公司价值定价。我们在在线附录章节OA.1中更正式地讨论了折旧，并表明当折旧为满值(δ = 1)时，公司现有资产的风险没有分散。

在假设1-4下，我们可以以封闭形式求解模型的动力学。附录a . 1给所有的证明。

定理1 平衡

均衡政策和价格有以下公式：

 

在表达式(16)-(18)中，前乘kj, ij和pj的项包含了分配和价格的随机成分。这些随机成分是下面定理的关键。重要的是，它们不依赖于资本质量冲击χj。在不含χj的全DSGE模型中，式(16)-(18)中相同的随机分量构成了各变量的随机趋势，如附录A.2所示。层特定的项nj,kj, ij，和pj是常数，因为消除了过渡时期。

在式(18)中，Dt是捕捉总需求的随机分量。它源于家庭，相当于家庭消费的总增长，在均衡状态下，这取决于所有层次的生产力冲击。术语Sj,t捕捉了在j层上运行的供应效应，因此取决于与j相关的上游各层的生产率冲击。表达式(18)表明Dt (Sj,t)增加(下降)均衡价格Pj，我们将在本节后面阐明。

当考察公司在一定规模回报下的估值时，我们感兴趣的是托宾q。给定定理1，我们可以在下一个定理中推出托宾q:

定理2 估值比率

定义公司j∈{0，..N−1}为除值除以资本:

 

定理2的直观在于j层安装资本的影子价格与其相对投入价格Pj+1之间的关系。Pj+1表示第j层资本投入的额外新单位的成本。完全DSGE模型的最优条件是，资本的影子成本为Pj+1·??(ij)。直观地说，在j层更换一个安装资本单位的成本等于购买一个新资本的成本好于安装成本??在假设1下，没有安装成本。因此式(19)中的比率等于资本的投入价格:Qj =Pj+1。因此，式(20)中的最后一项由均衡价格P j+1.16得到。括号中的项有两个分量。第一个来自Dt，而第二个负项来自Sj,t。重要的是，因为没有资本调整成本，没有与投资相关的租金，没有增长期权的价值。在简化模型中，企业估值仅反映了现有资产的价值。这个观察，连同定理2，产生以下推论:

推论1 用qjt衡量的j层公司的资产的对数估值(影子价格)随着其以下(上面)层的生产率冲击增加(减少):

 

我们把分析分成几个案例。第一种情况(l≤j)表明,如果两层,j和k,垂直位置高于l层(例如,j, k≥l),然后层l的生产力增加了估值的资产,j和k。这符合l层作为一个直接或间接客户。因此，l层生产率的提高会增加对两者资本产品的需求。重要的是，下游生产力冲击l使j和k的估值增加了相同的数量(注意，在公式(21)中，暴露与j无关，而对所有j,k >l都是相同的)。在仅仅改变需求的冲击风险暴露中，各层次之间不存在异质性。为了理解原因，假设第l层的生产力提高了。第l层的企业希望增加投资，因为它的边际生产率更高。然而，由式(15)可知，在平衡状态下，l+1层的劳动随时间而固定。再加上第l+1层的资本是预先确定的，第l+1层不能为l的投资生产更多的资本货物。因此，l的资本投入的价格，Pl+1，必须与l的生产率的增长完全成比例地增加，以抑制l的更多投资。接下来，考虑更高的P?在第l层+1。产出价格的上升会增加l+1的边际收入，就像生产率的上升一样。由于资本的边际收益较高，它希望进行更多的投资。同理，第l+2层不能提供更多的资本品，因此，Pl+2的价格必然与Pl+1的价格上涨相同比例。这个参数可以向上递归地重复。因为所有的相对价格都以相同的比例增长，并且这些价格等于下面一层的Q，在不同的公司中，对于影响公司需求的冲击，现有资产的暴露是相同的。通过平衡增长，暴露等于消费增长对l冲击的弹性。

 

为了解释TMB利差，我们对冲击的差异敞口感兴趣。这种差异可以解释任何两个层次j和k之间风险溢价的异质性。从上面的讨论中，这种溢价的差异不能用暴露于(相对的)下游冲击的情况来解释，而下游冲击纯粹诱导公司j和k的需求效应。因此，在本节的其余部分中，我们将重点讨论企业的资产暴露于(相对)上游冲击(作为企业的供应冲击)，以及累积的差异供应效应。

推论1的第二种情况(l>j)表明，如果j层的垂直位置低于l层，那么l的生产力降低了j.17的安装资本估值为了理解这种直觉，我们从l是j (l=j +1)的直接提供者开始。当j +1层生产率提高时，j的资本投入供给曲线向右移动。它给j的固定资本的估值带来了下行压力。这是因为j +1的技术进步使得j的资本投入的生产更容易、更便宜，降低了其资本重置成本。在完全竞争条件下，这会侵蚀j的现有资产的边际价值。我们将正向生产力创新对下游层现有资产估值的负面(供给)效应称为垂直创造性破坏。

垂直创造性破坏V仍然适用，尽管大小不同，当l是j的间接提供者时。假设l>j +1。当l的生产率提高时，不仅可以更便宜地替换直接客户的资本，而且可以更便宜地替换其客户的资本，客户的资本，三阶客户的资本等等。与直接情况一样，更换成本的下降会对安装资本产生负面影响。然而，这种垂直创造性破坏对于所有(相对的)下游层次来说并不是均匀的。相反，传播的衰减速率为α，即资本占产出的份额。要看到这一点，请注意(22)式中j层和j−1 层的负项之间的比率=α。这是因为，为了代替一个客户的客户的一个单位资本，只有α的支出支付给资本投入，其余的支付给劳动支出。虽然当我创新时，前者更便宜，但后者不受影响(由公式(15))。

 

重要的是，在假设1-3中是随时间固定的，在全量程DSGE模型中是随时间变化的。当I j不再是一个常数，同时存在调整成本时，就会发生这种情况。我们稍后将在第5.2.3节讨论这个问题。

 

为了评估来自直接供应商和间接供应商的累积垂直创造性破坏效应，我们需要对生产力冲击的相对强度采取立场。为简单起见，下面的定理是在假设2下导出的，即不同层的生产率之间存在完美的相关性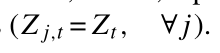

 

定理3 单调性

如果。则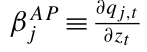在j中单调递增。

因为供给效应(垂直创造性破坏)从一层向下传播l所有底层层j < l速率为α，因为一个公司在层j < k有更多的直接和间接供应商,累计垂直创造性破坏从积极的共同创新是大j k。专注于极端,一个公司的底部生产链主题是最垂直创造性破坏的力量。它现有的资本是用它上面所有层产生的资本货物建立起来的。当每一种中间资本商品的生产成本变得更低时，供给效应就会累积向下传播，底层企业的资产价值将面临最大的下行压力。相比之下，处于生产链顶端的企业没有供应商，也不受这种创造性破坏力量的影响。

定理3的一个等价解释是垂直创造性破坏起到了对冲的作用。它通过减弱正的、同质的需求效应，使企业的安装资本对生产率冲击不那么敏感。累积供给效应在底层更大，因此正向生产力冲击使顶层企业的已安装资产价值比底层企业更高。顶级公司的资产估值更具周期性，因此风险更大。如定理3所示，风险度随垂直位置的增加而单调增加。

定理4表明，纵向创造性破坏的程度不仅取决于企业在生产链中的相对位置，还取决于生产链的长度。

定理4 链长和风险 

假设，我们有

1. 风险敞口。用表示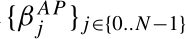中最大和最小风险暴露量的差值。生产链越长，风险暴露的分散性越大，即βAP随N的增加而增大。
2. 随机贴现因子。给出了用于确定股利要求价格的均衡对数随机折现因子

 

其中E为正标量，λ(N)为生产率风险的价格，εt+1为常见的生产率冲击。风险价格λ(N)随链长N而增大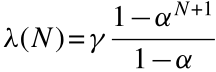

 

定理4表明，随着链长增加，顶层和底层生产率的差异增大。生产力风险的市场价格为正，且随链长增加而增加。结合顶部和底部生产率beta值的正差(第一部分)，以及正的风险价格(第二部分)，TMB息差应该是正的，而且在包含更多生产层次的网络中，其他条件都相同，TMB息差应该更大。

估计整个DSGE模型的风险溢价

为了便于处理，我们在封闭模型中假设，企业在做出投资决策后，会受到质量冲击。这与完全DSGE模型的设置不同，在该模型中，企业不受质量冲击的影响。然而，定理4中导出的封闭形式SDF为完整模型中的SDF提供了一个近似使用这个SDF，我们可以分析地为不受质量冲击影响的股息流定价，这更接近于一个公司在完全DSGE模型中的股息流。定义这个股息流的增长通过，其中​​​​​​​为闭形式模型中第j层企业的周期-t股利。注意，因为​​​​​​​(和​​​​​​​)是​​​​​​​的函数，乘以​​​​​​​可以中和资本免受这种质量冲击的影响。一个公司的预期回报，支付​​​​​​​在每个时期在定理5中给出:

定理5 预期的股息回报要求

让是支付股息的一个公司​​​​​​​每个时期的预期回报。假设εt为标准高斯分布。已知定理4中的​​​​​​​，随着j增加。

定理5表明，期望收益随着垂直位置的增加而增加。这与风格化的事实1在质量上是一致的。在下一节中，我们将校准整个DSGE模型，以检验垂直创造性破坏的量化力量，以解释这一事实。

5 定量结果

5.1 校准

表3显示了全DSGE模型的参数选择，按年频率校准。

生产参数:我们将N设置为5，意味着6个生产层，与基准经验结果类似。我们设α =0.33，使得不同层次的劳动产出占比为2/3。年折旧率为10%。资本调整成本参数φ有助于产出增长与数据的自相关性匹配，提高股票溢价的波动性。为了瞄准这些时刻，我们将调整成本设置为25。虽然这是一个相对较高的参数值，但重要的是要强调，我们在敏感性分析中证明，价差并不在数量上或质量上取决于这些调整成本的存在。

技术:为了降低外生模型参数的维度，我们假设所有生产力冲击都是完全相关的

 

这意味着，其中Zt是集合(共同)生产率。在Croce(2014)之后，总体生产率的对数增长动态，​​​​​​​，具有一个持久的组成部分:

 

 

其中分别为短期和长期总生产率冲击，它们的同时期相关性为​​​​​​​。为简单起见，设​​​​​​​= 1。这将模型中的冲击数量减少到只有一个标准高斯冲击。在上面的规范中，x指的是生产率增长中的长期风险成分。对于获得高股权溢价而言，这部分在数量上很重要，但在质量上并不重要。

 

 

 

总生产率对数增长μz被设置为消费的平均增长率约为2%，与数据类似。我们将σz设为1.7%，以获得略低于2%的消费增长年度波动率，这与长期样本当量一致。为了保持消费的长期成分较小，我们强加φx为0.085。这是一个保守值。Croce(2014)表明，在1930-2008年的样本中，长期风险波动率与短期风险波动率的比值约为10%。我们将长期分量ρx的持久性设置为0.98。这个值被设置为匹配消费增长与数据的自相关性(约为0.5)。

偏好参数:我们将相对风险厌恶和跨期替代弹性(IES)分别设为10和2。我们使用的IES大于统一，与最近的实证估计一致(见，例如，Bansal, Kiku，和Yaron 2012;Colacito和Croce 2011)。IES之所以重要，只是因为它在生产率增长中具有长期风险成分。我们将主观时间折现系数设为0.98，以目标为真实无风险利率水平。

5.2 模型结果

标定后的模型采用三阶摄动法求解。附录A.2显示了一级条件和所需的去趋势。

 

我们现在提出了校正模型的含义为总体宏观经济和资产定价时刻，以及层投资组合。根据封闭形式的结果，对模型的机理进行了检验。

5.2.1汇总宏观和定价时刻

表4比较了模型所隐含的总体宏观经济和回报矩与它们的实证对应项。模型隐含矩是从模拟的种群路径计算的。Panel A报告消费、产出和投资增长率的汇总统计数据。

所有宏观数据的增长率大约为每年2%，与数据一致。模型中消费增长的波动性为1.75%，而数据中为1.33%。虽然模型隐含的消费波动率略大于数据，但仍处于保守低水平，与消费增长波动率的长期样本估计值一致该模型隐含的产出波动率为2.11%，落在经验95%置信区间内。投资的波动性大于消费或产出的波动性，这与数据一致，但小于数据点的估计。这种低波动率不是源于资本调整成本，而是源于价值加权聚合方法。总投资波动率主要由最大层0层的低投资波动率驱动，即每年3.05%。在单一部门经济中，产出同时用于消费和投资，而在我们的模型中，第0层的产出仅用于消费。保持消费波动率低限制了0层的销售和投资变异性。重要的是，对不同层次的投资增长率进行平均加权计算，每年的波动率为5.05%，更接近实际数据模型中消费和产出的自相关系数分别为0.45和0.30。这与消费和产出增长的经验估计值0.52和0.28惊人地接近。投资的自相关系数在实证的95%置信区间内。

该模型还生成了合理的总资产定价矩。该模型中的股权溢价是5/3的倍数，以计入财务杠杆。模型隐含的股权溢价为每年4.13%，接近于实证的4.89%。模型偏离数据的一个维度是市场超额回报的波动性。在一般均衡生产模型中很难产生高股票溢价和高股票收益波动(见戈麦斯、科根和张2003的相关讨论)。非微不足道的股权溢价是通过相当大的风险厌恶值10，以及与Bansal和Yaron(2004)和Croce(2014)类似的持续生产率增长成分产生的。模型和数据中的无风险率约为每年1%，年波动率非常保守，为1%。IES加剧了股票回报的波动性，同时保持低波动率的无风险率。

5.2.2垂直位置和横断面收益影响

事实1:模型与数据

我们的第一个程式化事实表明，顶层(第5层)和底层(第0层)之间的超额收益率差约为每月105个基点，或每年11.27%(连续复合)。我们的模型成功地复制了这个相当大的价差，与定理5的逻辑和含义一致。表5报告了不同层次的模型隐含平均超额收益，与实证估计相比。模型暗示5层和0层之间的收益差为每年12.49%，这是令人印象深刻的大，并且在经验置信区间内。模型隐含的平均超额收益从第0层到第5层单调增加，并落在所有层数据的95%置信区间内。该模型为第1层、第4层和第5层产生了与数据惊人相似的超额收益。

事实2:模型与数据

我们的第二个风式化事实是，层投资组合对总生产率的暴露随垂直位置单调增加，而TMB分散的负载对总生产率呈正相关。我们通过对生产率的线性和二次项的投资组合超额回报的预测，获得模型隐含的生产率贝塔，就像我们对经验数据所做的那样(表2面板B)。在我们的实证分析中，我们使用两种方法来衡量总生产率。第一个是由Zt给出的希克斯中性生产率(索洛残差)。潜在的TFP可能无法观察到，因此我们还在模型中计算了相当于劳动生产率的度量。这是通过将每一层的销售额除以其劳动力，并在各层平均来实现的。我们在表6中报告了模型隐含的TMB生产率beta与实证对应值。在线附录的表OA.12显示了TMB beta在每个层的生产力暴露中的细分。

 

 

模型隐含的beta显示了几个与数据一致的模式。首先，在定量上，模型暗示的TMB beta具有相似的量级。例如，TMB beta到Solow残差(等于第5层和第0层之间的beta差)在数据中是1.93，而在模型中是2.16。其次，二次生产力项的系数在模型和数据中都是非零的。在模型中，由于风险的时变，收益和生产率之间的关系是非线性的。我们在下一小节进一步解释这一点。第三，TMB贝塔的分解，如表OA.12所示，表明模型隐含的生产率贝塔从第0层到第5层单调增加，与数据一致。

 

5.2.3 机制检查

托宾q定理3的差异暴露表明，生产力冲击对顶层托宾q的影响比底层强。在完整的DSGE模型中也是如此，如表7所示，表7报告了校准模型中0到4层企业的生产率弹性。与定理一致的是，随着垂直位置的增加，托宾q对生产力冲击的敏感性单调增加。

我们可以把托宾q的弹性分解为两个分量。所有层的最优性条件规定，∀j∈{0，…，4}。这说明托宾q的变化可以归结为新资本价格的变化(Pj+1)和资本安装成本的变化()。宽泛地说，前者与公司的现有资产价值有关，而后者与公司的租金和增长选择有关。

表7显示，积极的生产力冲击增加了所有层次的新资本投入的相对价格。这种积极的敏感性是需求效应的结果。然而，底层的资本投入价格上涨幅度较小。这与式(18)一致，是对底层现有资产进行更强的垂直创造性破坏的结果。

在第4节中，简化的假设1和假设3暗示企业的投资率是固定的，不存在调整成本。这导致了两种结果。首先，没有增长期权价值(​​​​​​​= 1)对于处于第4节的封闭形式均衡的企业。第二，企业对总生产率的敞口是固定的(见公式(21)和式(22))。

通过层特定冲击的机制的数值说明

为了节约起见，我们的基线模型以单一电击为特征。TMB的存在并不取决于对单一冲击的假设。为了说明这一点，并进一步说明推论1中所描述的垂直创造性破坏机制，我们现在采用第4节的假设2:对于j∈{0，每一层都受到一个特定层冲击Zj(即)，其中所有Zj冲击正交。为简单起见，我们将所有层生产率Zj冲击的漂移和波动值校准为与基准模型中的总生产率相同的值。

所有层次特定的冲击都是系统性的，并在均衡中带有风险溢价。我们得到的模型隐含的TMB息差仍然为正且可观，为每年4.37%。只要将冲击的波动性提高到上层(与数据一致)，同时保持消费的波动性较低，就可以提高这种利差。表8报告了第j层企业对第k层生产力冲击的暴露情况

与式(21)一致，如果冲击来自直接或间接供应商，企业对其有负向暴露，符合垂直创造性破坏。​​​​​​​，与式(22)一致。它源于公司的直接或间接客户增加的需求效应。尽管这些迹象是一致的，但由于投资率和调整成本的时变，敞口的大小偏离了表达式(21)和(22)，这在第4节中没有提到。与式(22)一致，当冲击来自企业的直接供应商时，供给效应更强，当冲击来自企业的供应商或供应商时，供给效应减弱，对于高阶供应商则进一步减弱。为了说明所有冲击的累积效应，表8的最后一列总和了每一层对所有特定层技术冲击的暴露。如果假设各层特定冲击之间的相关性为1(如定理3中所示)，这个总和(以一种相对静态的方式)捕获了企业对总生产率的暴露程度。与基准模型一致，隐含的总生产率系数随着垂直位置的增加而增加。

资本资产定价模型α 在校正后的模型中，所有层都受到共同生产力冲击的影响。然而，无条件资本资产定价模型(CAPM)在模型中不成立，因为在潜在冲击中估值是非线性的。正如前面所讨论的，非线性可以用企业对总生产率的beta值是时变的这一事实来解释。我们发现模型中的杠杆CAPMα为每年6.7%，约占利差的52%。当模型特征层特定冲击时，作为整体模型隐含价差百分比的CAPM alpha可以进一步提高。在上述模型扩展中，CAPM alpha和模型隐含的TMB之间的比率约为70%。由于每一层的生产力都是在截面上定价的，因此，即使是有条件的CAPM也无法解释这种差异。

敏感性分析 在在线附录章节OA.1中，我们对模型的结果进行了关键参数的敏感性分析。我们证明了对TMB价差的标志具有定性重要意义的唯一参数是跨期替代的弹性，它决定了替代效应的强度和/或市场价格或风险的标志。其他参数，例如是否存在生产率的长期风险或调整成本的大小，只是在数量上很重要。特别是，TMB价差并不取决于资本调整成本:在没有这些成本的情况下，价差大于基准利率。直观地说，在没有调整成本的情况下，企业从现有资产(增长选项的权重为零)获得其全部估值。由于现有资产是公司的组成部分，它会受到垂直创造性破坏，传播被放大。出于类似的原因，当折旧参数下降时，价差被放大。

1. 测试机制:模型预测和启示

我们做了几个垂直创造性破坏机制的测试。首先，我们比较模型和数据之间的资本投资、投入价格和托宾q的周期性。其次，我们研究了市场力量对TMB扩散和底层企业收益的影响。第三，我们检验了子样本中的TMB价差，并证明，对于那些资产在其价值中所占比例较大的公司，价差更大。

6.1检验模型对资本和价格动态的预测资本投资和销售的周期性 我们证明了模型隐含的销售和资本投资的周期性与数据一致。设为时刻j层的一个感兴趣的变量。用表示时刻t的总生产率的时间序列。构造一个向量Yt =向量中的第一个变量是生产率y变量，包括投资率和销售额(按资产比例)，按垂直位置递减排序我们估计了向量Yt的VAR(k)模型，其中滞后k为1年(在年频率上模拟模型路径k = 1，在季度频率上经验数据k = 4)。所有变量在包含在向量Y之前，都通过其标准差标准化。

在模型中，我们将设为总生产率增长。在数据中，我们使用第2.2节中描述的索洛残差，这是最接近的实证对应。为了评估周期模式，我们感兴趣的是1个标准差的Cholesky冲击对y0,t和y4,t的影响。脉冲响应函数(IRF)揭示了y是在链的顶部还是底部更具周期性。我们在在线附录的表OA.13中报告了最下游的层(0层，称为“底部”)、向量Y中最上游的层(4层，称为“顶部”)和中间层(2层，称为“中间”)。

在模型和数据中，对生产率的1个标准差的冲击使顶层企业比底层企业更能提高未来一年的投资率。两者的幅度是相似的。标准化冲击使模型隐含的上(下)投资率增加了0.21(0.09)个标准差。在数据中，数字分别为0.24和0.11。在一个积极的生产力冲击之后，家庭希望储蓄更多，因为替代效应占主导地位(ψ >1)。其结果是，资源更多地分配到上游层，顶层的投资率上升更多。该模型特征与表7最后一列一致。数据显示类似的模式这一事实为我们的模型提供了实际支持。

在跨层销售的冲动反应中也出现了类似的模式。积极的生产力冲击对顶层企业的销售有更大的影响。在模型和数据中，irf的大小与投资率的irf相当相似。逻辑是相似的。由于更强的替代效应，积极的生产力冲击将劳动力转移到上游层次。考虑到资金是预先确定的，顶层的销售增长高于底层。

 

托宾q和投入价格的周期性 从表7可以看出，在我们的模型中，上游企业的托宾q和投入价格比下游企业更具顺周期性。为了检验这一预测，我们将每一层的托宾q的季度变化回归到总生产率的变化上。表2显示了线性模型(面板a)和包含线性和非线性项的模型(面板B)中每一层的暴露情况。在两个面板中，我们使用了两个替代生产率代理，劳动生产率和索洛残差。结果强烈支持模型预测:无论使用哪种生产率代理，两种模型的Tobin’s q的敏感性从第0层到第5层几乎单调增加，且顶层和底层之间的差异具有统计学意义。

模型所暗示的投入价格的周期性模式与Kogan, Li, and Zhang(2018)一致，他们认为投入价格更具顺周期性，对总体冲击更敏感(主要影响下游企业和消费者)。在在线附录章节OA.4中，我们使用劳工统计局产生的中间需求的投入价格指数，表明上游投入价格在行业水平上具有更高的周期性。

6.2垄断竞争对垂直创造性破坏的影响

我们的基准模型以完全竞争为特征。垂直创造性破坏源于竞争对手以较低成本替换现有资产的能力，因此这种影响可能在完全竞争的环境中最强。在这一节中，我们从实证和理论两方面研究了企业的市场支配力如何影响TMB传播。

6.2.1 TMB传播:高竞争vs低竞争 为了进行测试，我们首先开发了一种新的供应链竞争方法。FactSet Revere关系数据集允许我们识别每家公司自己或其竞争对手报告的竞争对手。我们利用这些数据构建了一个新的竞争衡量方法，该方法不仅考虑了企业自身的竞争环境(以竞争对手的数量为代表)，而且还考虑了其直接和间接供应商所面临的竞争在线附录OA.3为该措施的构建提供了进一步的细节。我们利用供应链竞争测度将每一层的企业分成两个子样本。高(低)竞争子样本包括衡量高于(低于)其层中值的公司。我们计算每个子样本的TMB价差。

为了比较这种实证分裂与模型，我们扩充了具有垄断竞争特征的基准模型。在线附录OA.2部分介绍了该模型。在增广模型中，参数μ表征竞争的程度。对于μ，我们考虑两种选择:(1)高竞争情况下:μ= 100，意味着1%的加成;(2)低竞争情况下:μ=3，意味着33%的加成。这些数字与加成的实证估计是一致的(例如Bilbiie Ghironi和Melitz 2012)表10提供了结果。

当企业在模型和数据中都拥有更大的市场支撑力时，TMB价差就会下降。高(低)竞争子样本的经验价差为9.97% (4.63%)p.a。这些子样本的模型隐含价差在定性和定量上与数据相似。对于高(低)竞争校准，模型隐含的TMB为12.15%(7.9%)。模型暗示，对于高竞争子样本中的所有层，以及除了一个低竞争子样本中的所有层，超额收益都落在经验95%置信区间内。

 

结果表明，当企业及其供应商拥有更大的市场支配力时，TMB价差下降。有两种力量导致了这个结果。首先，保持企业供应商的市场力量不变，随着企业自身垄断力量的增强，垂直创造性破坏减弱。在完全竞争条件下，公司的估值取决于其资本存量的重置成本。在垄断竞争下，估价也依赖于垄断租金。技术改进所带来的好处并没有受到竞争的侵蚀。对下游企业来说，技术改进降低了投资成本，提高了租金。这种现金流效应抵消了对现有资产的负面影响。

• 保持企业的市场支撑力不变，当供应商的市场支撑力增加时，纵向创造性破坏就会减弱。当供应商具有较高程度的垄断权力时，它对其生产产生配给效应。在对正生产力冲击的响应中，供应商的产出增加比完全竞争情况下要少。因此，企业资本投入的供给没有上升那么多，减弱了垂直创造性破坏。

6.2.2供应商竞争力与底层退货

如上所述，供应商的市场力量越大，下游企业就越容易受到生产力冲击。因此，我们认为企业直接和间接供应商的市场力量与其自身的股票收益之间存在正相关关系。拥有更有竞争力的供应链的公司更易遭受更强的垂直创造性破坏，因此，应该更少地暴露于生产力和赚取更低的回报。为了检验我们的增强模型的这一新颖预测，我们将底层企业进行了拆分，这些企业属于消费必需品和非必需消费品部门，根据模型，它们是受垂直创造性破坏影响最大的主体，26 .根据直接和间接供应商的竞争对手的平均数量分为五组组1代表供应商竞争力最强的公司，而组5代表供应商竞争力最差的公司。与我们的预测一致，表11显示底层企业的价值加权收益从第1组增加到第5组。这两组间的差异为4.37%，具有统计学意义。这一发现与我们的机制是一致的，并表明供应商面临更多(更少)竞争的公司显著更低(更高)回报。

 

6.3到位资产对垂直创造性破坏的重要性

垂直创造性破坏影响到位资产的价值，所以当到位资产在企业价值中所占比例较大时，其作用更强。这意味着这些公司之间的TMB差距更大。在联机附录章节OA.1中，我们使用模型比较静态来演示这种直觉。表OA.1显示，当我们降低折旧率或调整成本时，TMB比基准情况下要大。这些结果表明，当企业从现有资产中获得更大比例的估值时，价差就会被放大。我们在下面以经验来证实这一点。

账面市值比和折旧:账面市值比和资本折旧率是衡量公司价值中现有资产权重的两个指标。较高的账面市值比或较低的折旧率意味着较高的现有资产权重，因此，更大的TMB利差。

 

为了检验这一预测，我们根据这些比率将每一层的公司分成两个大小相等的子样本，并在表12中报告每个子样本中的TMB分布。结果与我们的假设一致。表中Panel A显示价值型公司的价值加权TMB和等加权TMB价差分别为11.9%和16.0%，而成长型公司的相同价差分别为8.2%和3.1%。图B显示，低折旧样本的价值加权TMB价差比高折旧样本的价差高出8% (14.0% vs. 6.0%)，尽管等量加权TMB价差的差异很小。

组织资本:Eisfeldt和Papanikolaou(2013)区分了两种类型的资本:物质资本和来自关键人才的组织资本。组织资本是与专业化劳动投入相关联的，而不是由供应链上的供应商提供的，因此供应商的创新不应该影响其估值。换句话说，它不受垂直创造性破坏的影响。因此，对于拥有更多组织资本的公司，TMB的价差应该更低。表12 Panel C显示了支持该假设的结果。对于低组织资本样本，TMB价差较大且具有统计学意义(价值加权9.3%)，而对于高组织资本样本，TMB价差接近于零。

库存:与实物资本的库存类似，库存的库存也会受到垂直创造性破坏。因此，我们的模型表明，在拥有更多库存的企业中，TMB的价差应该更大。表12面板D的结果证实了这个猜想:对于高库存子样本，TMB价差为12.0%(价值加权)或13.3%(等加权)，在5%水平上有统计学意义，但在低库存子样本中不显著。

作为一个额外的测试，我们检查层返回在每个子样本的单调性。在线附录中的表OA.14表明，无论是价值加权组合还是等加权组合，高账面市值比、低折旧、低组织资本、高库存子样本的单调性较强，垂直创造性破坏较强。然而，在具有相反企业特征的子样本中，它就弱得多。这进一步支持了垂直创造性破坏作为回报扩散到垂直位置的驱动力。

7 稳定性

7.1 使用代替数据库的TMB

我们的基准测试结果基于FactSet Revere数据库。该数据库在公司层面上提供了供应商-客户/竞争对手关系的最全面的覆盖，这使我们能够在公司层面上准确地度量上游。然而，它涵盖了一个相对较短的时间周期，它不允许我们构建一个垂直位置的衡量，考虑到每个供应商-客户关系的强度。在本节中，我们将使用允许我们克服这两个限制的替代数据库来演示TMB传播的健壮性。

7.1.1使用投入产出表的行业间结果 

东亚经济分析局定期发布投入产出账户，提供行业间经济关系的快照。每个快照由两个表组成。“制造”表格显示了以美元为单位的各个行业的商品产量。“使用”表显示了每个行业每种商品的使用情况，也以美元价值计算。我们在每个时间点使用use和Make表的组合来计算行业级别的垂直位置。我们遵循Antràs等人(2012)计算每个行业垂直位置的方法。这种方法考虑了行业之间每个联系的强度。在线附录OA.6部分解释了上游措施的建设细节。

由于详细的I-O表每5年才提供一次，所以我们使用对第t年计算的行业垂直位置来确定企业从第t - 4年到第t年的垂直位置，基于它们的行业从属关系。我们从1974年1月开始抽样，因为我们的CRSP数据库中的公司数量在今年之前显著下降。能提供详细I-O表格的最后一年是2012年。为了将基于行业的结果扩展到2017年，我们将属于行业i的firm在2013年至2017年的垂直位置得分指定为2012年计算的最新垂直位置得分。

 

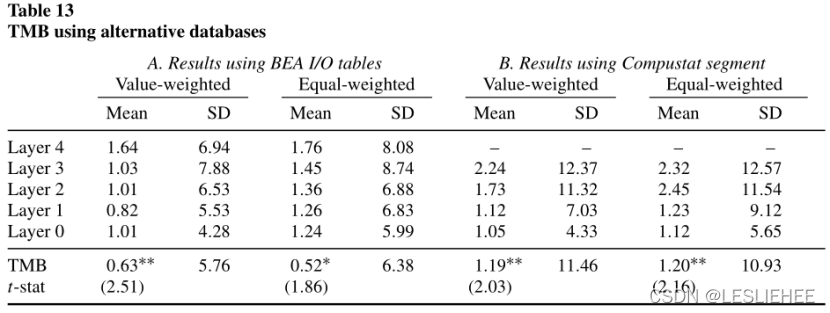
基于I-O数据的TMB价差并没有涵盖同一行业不同垂直位置企业之间存在的价差。这种行业内的差距可能很大，这也是表13面板A中较低的TMB的部分原因。为了说明这一点，我们确认TMB扩散存在于我们样本中的三个最大的非消费部门:工业(GICS=20)、卫生保健(GICS=35)和信息技术(GICS=45)。对于每个部门，我们将样本限制为属于该部门的公司，并检查部门内部TMB。在未列出的结果中，我们发现每个行业的TMB息差超过每月90个基点。这就强调了TMB价差中行业内成分的重要性。

7.1.2使用Compustat Segment数据库的结果 在公司一级连接供应商与客户的另一个来源是Compustat Segment数据库。它只报告关键客户，因为供应商只需要报告占其总销售额10%或以上的客户。利用该数据库，我们证实了企业垂直头寸与其风险溢价之间的单调关系，以及相当大的TMB利差。

我们根据公司的垂直头寸在每年的12月将它们划分为投资组合，并在1月至12月期间持有这些投资组合。与BEA分析一样，我们将垂直位置标准化到[0,5]段上，并使用{1,2,3,4}作为断点。然而，由于Segment数据中的缺失环节，观察到的供应链明显更短，落入第4层的公司数量也过于稀少。因此，我们将第3层和第4层的公司合并为一个单一的顶层，形成四个投资组合。表13中的Panel B报告了投资组合的月度收益。结果证实了我们的基准分析。值得注意的是，价值加权和等加权TMB价差的幅度与FactSet数据所暗示的价差相似，约为每月1.2%，显著性为5%。从第0层到第3层，价值加权收益单调递增。

7.2 组合形成方法的稳健性

我们证实了TMB价差对于形成组合和计算垂直位置的其他方法是稳健的。结果如表OA.16所示。在第一列和第二列中，我们分别每季度或每年根据公司的垂直头寸对其投资组合进行一次分类。TMB传播仍为阳性且显著。为了让关系信息有更多的时间被股票价格吸收，在第3列中，我们根据在第t−4月底计算的垂直位置，在每个月的月初将公司分类到投资组合中，而不是在基准执行中的第t−2。结果基本上没有改变。

在基准情况下，我们将企业的垂直位置定义为企业与底层之间的最小距离。在表OA.16的第4列中，我们使用到底部的中间距离来计算垂直位置。在这种替代方案下，TMB为77 bps，显著性为10%。顶层和第一层之间的差距为92个基点，在5%的水平下显著在表OA.16的第5列中，我们将层数从6个减少到5个。所有垂直位置在4或以上的公司都被分配到顶层。TMB传播较小，但仍为阳性，且在10%水平上具有统计学意义。

在在线附录的表OA.18中，我们仅根据企业的第一次垂直位置观察将企业划分到各层，并在整个样本期间保持企业的投资组合分配不变。定性地说，我们仍然得到平均收益与垂直位置之间的单调递增模式。TMB息差为每月41个基点，但在统计学上不显著。垂直位置在很大程度上是一个持久性度量，但它的时间变化保证了动态排序。我们还在未列表的结果中证实，当我们排除能源和材料行业或仅使用耐用品生产商作为底层时，价差存在。

8 讨论和替代解释

在本节中，我们考虑了我们模型和数据的几个额外特征，并讨论了TMB传播的其他解释。

企业跨层分布的金字塔形状:表14显示了各层企业的特征。一个明显的特征是，当垂直位置j上升时，j层的公司数量通常会下降。因此，与第0层相比，顶层的填充更少。虽然这种内生性金字塔形状可能捕捉多层生产经济的真实结构，但它引发了一个担忧，即TMB扩散是由于顶层和底层企业数量不均匀而机械地产生的。我们使用在线附录章节OA.9中的蒙特卡罗实验来排除这种解释。如果我们保持每个生产层中的企业数量与数据中的企业数量相等，但随机分配企业的垂直位置，则隐含的TMB分布与零难以区分。

网络中心性:处于不同垂直位置的企业中心性可能存在差异。Ahern(2013)发现网络中心性越高的行业收益越高。然而，表14的最后一列报告说，第0层的中心性比顶层的中心性高一个数量级。因此，我们不能将TMB扩散归因于中心性。

财务和经营杠杆:纵向地位越高的企业，其收益越高，可能是因为杠杆率越高。表14显示，顶层和底层之间的财务杠杆没有显著差异。此外，顶层公司实际上比底层公司的运营杠杆要低得多。

熟悉性假设:上游企业可能不为投资者所熟悉，存在更多的信息不对称和流动性不足。然而，表14显示，在买卖价差或盈利预测在各层之间的分散没有显著差异，表明顶层公司并没有更不透明。此外，机构所有权在上层低于下层，这表明散户投资者不会因为熟悉度较低而回避上游公司。

在在线附录章节OA.10中，我们考虑并排除了TMB传播的另外两种替代解释:(1)上层垂直位置的持久性较低，(2)“牛鞭效应”(Lee, Padmanabhan, and Whang 1997)与上层企业更大的需求预测误差相关。

9 结论

结论利用新型的FactSet Revere数据库对企业在生产网络中的垂直位置进行了测量，并记录了两个程式化事实。垂直位置越高的企业，其股票收益越高;(2)更多地暴露于总生产率。顶部和底部之间的息差是每月105个基点。在1980年代开始使用Compustat Segment数据库构建的较长的样本中，价差的大小几乎相同。从上世纪70年代开始，根据东亚银行的投入产出表衡量的行业间TMB息差为每月63个基点。

我们使用封闭式模型和定量一般均衡模型对这些新发现提供了基于风险的解释。当各个生产层次的公司从提高的生产力中获得直接利益时，这种利益被对现有资产价值的向下供应压力所削弱，我们称之为垂直创造性破坏。底层企业受供应压力影响最大，因为它会向下游累积。因此，底层企业对总生产率的内在敞口较小。

我们对该理论进行了若干实证检验。托宾的q、投资和投入价格的周期性模式与模型一致。我们的模型也支持我们的机制和供应链竞争程度之间的交互作用。两种经验模式与以垄断竞争为特征的增强模型一致。首先，我们的实证研究表明，对于属于竞争较少的供应链的样本公司，TMB的价差较小。其次，我们记录了一个新的程式化事实:消费品生产商的直接和间接供应商拥有更大的市场支配力，从而获得更高的股票回报。我们还表明，对于从现有资产中获得更大比例价值的公司(例如，价值型公司)，TMB价差更大，因为这是受垂直创造性破坏的组成部分。

总的来说，我们记录了一些新的事实，将公司的上游和竞争环境与他们的风险联系起来。纵向创造性破坏可以定量地解释这些事实，表明它对于解释横向风险溢价差异的重要性。