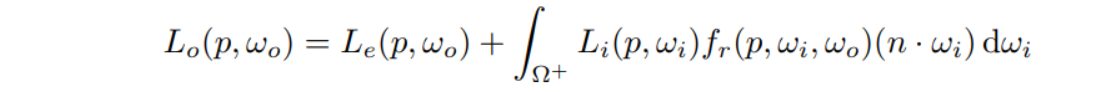光线追踪2 - 加速结构(Ray Tracing 2 - Acceleration)
- 对AABB结构优化来加速光线追踪的速度
- 均匀网格(Uniform grids)
- 空间划分(Spatial partitions)
均匀空间划分(Uniform Spatial Partitions)
上一节课中,使用了AABB包围盒的方式来判断物体,然后判断光线是否和包围盒相交,如果和包围盒相交,再判断是否和内部的物体相交。均匀空间划分就是直接使用了这个思想。
比如有下面这个场景:

- 先找到整个场景的包围盒

- 然后在进行任何光线追踪的计算之前,先对整个包围盒进行一个预处理,将其分为许多均匀的网格。

- 划分格子之后,判定哪些格子里可能有物体,即哪些格子和物体的表面相交。

- 处理之后,就可以知道哪些格子里有物体,然后就可以开始进行光线追踪,比如一条光线朝着右上方射进来,可以看到光线经过了一些盒子,有的盒子和物体有交点,有的盒子与物体没有交点。光线经过的与物体有交点的盒子,就判断光线是否和盒子内的物体是否有交点。也就是说光线只要进行若干次和盒子的求交,就避免了和场景中的所有物体进行求交,也就加快了速度。

- 也有人会问如何判断光线经过哪些格子,最最简单的思路是这样:因为光线是朝着右上方射入的,每次只要判断当前经过格子的右边,上边和右上边的三个格子即可。可以从中找到光线经过了哪些格子。这个过程其实就是在光栅化的过程中如何画一条线的方法。
这个结构的加速能力,其实就是多做一些光线与盒子的求交,从而减少光线与物体的求交。那么如何判断加速效果怎么样?可以看下面的几种情况:
- 只有一个1 × 1 的格子:如果只有一个格子,则还是要将光线与每个物体求交,没有起到加速的效果。

- 如果格子很密集,就会增加光线与格子求交的次数,效率也会降低。

所以格子的数量也不是越多越好,根据前人的实验经验可以得出,格子的数量最好如下:
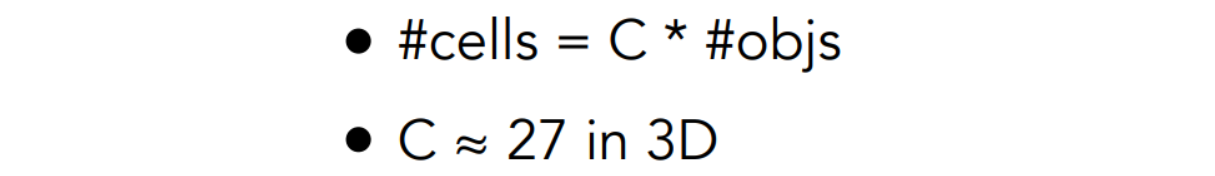
当场景中的物体比较密集时,使用这种划分为格子的效果很好,如下:

但是当场景比较空旷,就会出现一个问题,称作“在广场中的茶壶”问题(“Teapot in a stadium” problem) 。因为将一个空旷的场景划分为许多格子,而物体比较少,例如一个大广场之中只有一个格子里包含有物体的时候,再用光线和格子求交的效率就会很低,如果在都是空气的地方都用大一些的格子,而在物体比较密集的地方用小一些的格子,这样就能够获得一个更好的效果,所以就需要别的方法。
空间划分(Spatial Partitions)
空间划分有以下几种方法:

- Oct - Tree(八叉树):先用一个包围盒把整个场景包起来,然后切成八份(在三维空间中横竖一刀,一共就是八份,二维的空间上就是4份,如图),然后对每一个子节点,再切成四块,图中只画了左上角切了,其实每一个都要切。但是什么时候停下来不切了?有不同的标准,比如说右下角一大块什么都没有,就可以停下来不切了,左上角比较密集,就多切几刀。直到划分到某一个格子没有物体或者只有少数物体,就可以停下来了。这就把空间切成了一个不均匀的块,并且组成了一个树。但这个方法并不好用。
- KD - Tree :KDTree做的和八叉树类似,但是每次只沿着一条轴砍一刀,分成两块。不断重复水平一刀竖直一刀的过程。整个空间就被划分成了一个二叉树的结构。为什么要交替的进行水平和数值的划分?因为这样可以保证空间基本上是个均匀的划分方式,如果只沿着水平或者数值方向,则到最后就会把空间分成那种长条状的,这种划分方式就不好。如果三维空间种,就是先X轴,再Y轴,再Z轴的顺序进行划分。
- BSP - Tree:对空间是采用二分的方法,每次选一个方向,将一个节点劈成两半。但是空间会分为很多种斜的空间,因为采用AABB的方式能够比较容易的计算交点,斜着的空间计算交点比较麻烦,所以这个方法不好。维度越高越麻烦。
KD - Tree的预处理

KD - Tree的预处理的方式如上所示(在光线追踪之前完成)
- A是整个最大的包围盒,将A切成蓝色的1和包围盒B(实际上1也要再切,但是这里为了讲述过程,只需要切一边即可,下面也都是如此),并作为1的两个子节点
- B是由2、3、4、5组成的一个包围盒,将B水平切成C和区域2,并作为B的两个子节点
- C是由3、4、5组成的一个包围盒,将C切成区域3和包围盒D,作为C的两个子节点
- D是由4、5组成的包围盒,将D切成4、5,作为D的两个子节点。
我们可以看到,KD-Tree最终将整个场景构成了一个二叉树的结构,那么就需要考虑应该用什么样的数据结构来存储整个场景的信息。
KD - Tree的数据结构
- 非叶节点存储的数据:
- 划分轴:x,y,z轴
- 划分的位置:划分平面在空间中的坐标
- 指向子节点的指针
- 在非叶节点中不存储物体
- 叶节点存储的数据:
- 叶节点对应的区域内包含的物体
在KD - Tree处理好的区域中进行光线追踪

过程如下面几张图所示:






这整个过程就是在判断光线与树上的节点所对应的范围是否有交点,如果和一个子节点所在的范围没有交点,那么就不再判断光线和这个子节点所在的子树是否有交点;如果和一个光线和子节点对应的范围有交点,则:1.如果这个子节点是非叶节点,那么继续重复上面的步骤,判断该节点的子节点是否和光线有交点。2.如果这个子节点是叶子节点,则判断光线和该叶子节点中存储的物体是否有交点
KD - Tree的缺陷
- 由于每一个子节点都要存储在其对应区域内的物体的信息,就会导致同一个物体被多个叶节点存储,浪费了多余的空间。比如上图中一个圆与三个盒子相交,那么这三个盒子都要存储这个圆的信息。
- 判断三角形和盒子的相交存在一定的问题。比如说,如果认为一个三角形和一个盒子相交,只要三角形的某一个顶点在盒子里我们就认为三角形和这个盒子相交,但是会出现三角形的三个顶点都不在盒子里,但是三角形仍然和盒子相交,比如有一个很大的三角形将盒子包围了起来;这种情况下要建立KD - Tree就会比较困难。
后来人们发现了还有另一种办法可以避免上述的缺陷,所以就引入了物体划分
物体划分(Ojbect Partitions) - Bounding Volume Hierarchy(BVH)
BVH这种加速结构是目前运用最广泛的一种方法,其原理如下:

与上面的加速结构一样,需要先找一个包围盒把整个场景包围起来,并作为树的根节点。

然后根据三角形的数量,而并非是空间,将三角形分为两堆,再分别用两个包围盒包围起来,作为树的两个子节点。

接着再重复上面的过程,将包围盒的三角形分成两堆,左边的黄色区域也要划分,不过这里只是为了说明就没有划分。
这种方式就避免了KD - Tree中物体重复存储的问题,上面的图中可以看到,虽然三角形可能和其他的包围盒存在交集,但是每个三角形都只被一个包围盒完整的包围出来。不同的包围盒之间交集越少,则说明这次划分的效果就越好。关于怎么划分,很有讲究。
总结一下,BVH的过程就是:
- 先找到一个大的包围盒包围整个场景
- 递归的把包围盒根据物体的数量划分为两个部分
- 重新计算划分后的两个部分的包围盒
- 停止条件:达到必要的条件即可,比如:当叶子节点内部只要有足够少的三角形即可
- 物体依旧存储在叶子节点里
如何划分?
- 选择一个维度进行划分,比如现在x轴划分,再在y轴划分
- 选择包围盒最长的那个维度进行划分,比如有一个长条状的包围盒,就沿着垂直于这个轴的方向进行划分,尽量将空间的大小划分的均匀,而不是都是划分成长条状
- 选择中间的那个物体作为划分点。比如我有一排三角形,就选择在处在中位数位置的三角形作为划分点;或者说在空间上有许多三角形,我可以沿着某一个方向,比如沿着x轴方向求出三角形的中位数,以这个物体为基础划分。这样做的好处就是能够尽量维持两个包围盒中的物体相同,也就能尽可能平衡这颗二叉树,使最后形成的二叉树深度最小,减少了搜查时间。
- 如果场景动态或者场景发生变化,那就只能重新构建一个新的BVH
BHVs的数据结构
- 非叶节点存储数据
- 包围盒
- 子节点指针
- 叶节点存储的数据
- 包围盒
- 具体的物体
BVH算法

- 如果光线和子节点的包围盒没有交点,什么也不做直接返回
- 如果过交点是叶子交点
- 和包围盒内所有的三角形求交
- 返回距离最近的交点
- 否则再递归的和子节点求交,返回最近的节点
空间划分和物体划分的区别
空间划分:
- 将空间划分为多个不重叠的区域
- 一个物体可以被多个空间所包含
物体划分:
- 将物体划分为多个不相交的子集
- 每个子集的包围盒有可能与其他的包围盒重叠
辐射度量学(Basic radiometry)
Radiant Energy and Flux(Power)
Radiant Energy:Radiant Energy是光源辐射出来的能量的总量,单位是焦耳(Q)。
Radiant Flux : Radiant Flux是单位时间内,光源辐射出来的能量,定义式如下:
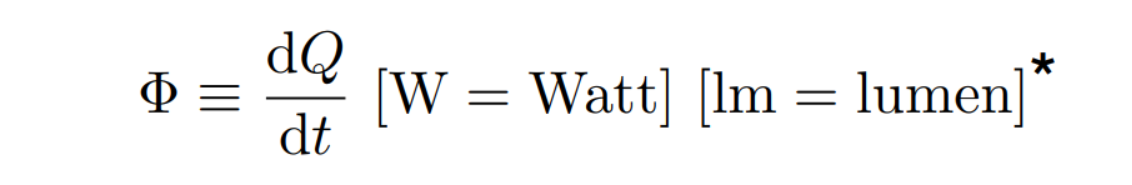
Radiant Intensity
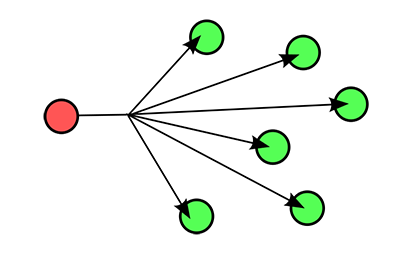
Radiant Intensity是单位时间内,光源向单位立体角(Solid Angles)所辐射出的能量。

角和立体角(Angles and Solid Angles)
角:角度对应的弧长/圆的半径

立体角:球的某一个角度范围对应的面积 / 球的半径的平方

单位立体角(Differential Solid Angles)

dA的推导过程可以参考三重积分的球面积分法的推到过程,dw的则是按照立体角的定义所得。
值得注意的是,将这个球的立体角积分最后得到的结果是4PI,并且立体角只做一个向量使用,使用立体角代表从球心发出的光线指向的方向。

其它关系:

上式代表,将每个立体角方向的randiant Intensity积分起来得到就是radiant flux.