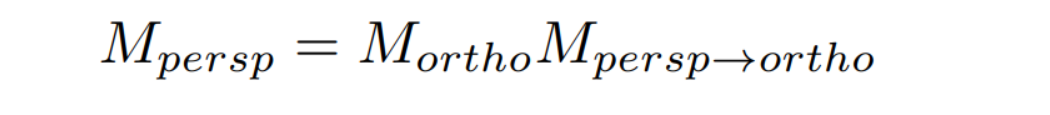着色2（Shading 2）

Blinn - Phong 光照模型包括 ： 漫反射、镜面反射、环境光。上一节讲了漫反射，下面讲一下镜面反射和环境光。

镜面反射（Specular reflection）

镜面反射：当物体的表面很光滑的时候，在一定的角度范围内观察这个平滑的表面表面时，能够看到一个高光的效果。

如在用光源照射金属时，在一定的角度内可以看到一个有一定大小的光点，但你偏离一定的角度之后，就不能再看到这个高光效果。

在漫反射的部分已经讲过，漫反射的着色与观察方向无关，而镜面反射不同，镜面反射的效果是与观察方向有关的。

当观察方向和光的反射方向越近的时候，观察到的镜面反射效果越强。

如何衡量两个上图中反射光和观察方向是否足够近？可以用反射光的方向向量和观察方向的方向向量做点乘，得到其夹角的余弦值，点乘的结果越大，则反射光和观察方向就越近。

上面这是冯氏光照模型的做法，Blinn - Phong光照模型是对冯氏模型的一个改进，下面是Blinn - Phong的做法：

这里并不是计算反射光和观察方向的远近，而是计算半程向量h和该平面的法向量n的远近。因为反射光和观察方向越近，半程向量和法向量也就越近，且计算反射光的计算量比较大，而半程向量h只需要将v和l相加，再标准化即可得到，计算简单。

最终计算某一点的高光强度的计算方法如下：

ks：反光系数，不同的材质对光的反射程度不同，如金属和木头对光的反射效果就不同。

指数p：先看下图：

可以看到指数越大，cos不为0的范围就越小。应该这样理解，如果p为1，那么在0 - 90°的这样一个范围内都可以看到一个高光效果，但现实生活中观察的偏离角度较大的时候就不能看到高光了，而随着p的增大，能看到高光的角度就会缩小，比如p = 1时，在45°就能看到高光效果，而p = 64时，在45°就看不到高光效果了。也就是说p越小，对高光的容忍度越高，但是我们平时看到的高光都是集中在一点并且是在一个比较小的范围内，所以用较高的指数p将高光限制在一个很小的范围内。

下图是ks和p对高光效果的影响，同一行使用的材质相同，同一列使用的p相同。

可以看到材质反光系数越大，高光越大；p越大，高光范围越小。

环境光（Ambient Term）

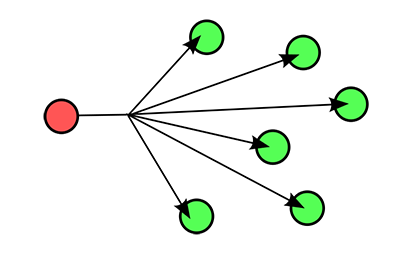
在上一节中层说到，环境光就是许多光线经过多次漫反射最终打在某一点上，因为环境光的太复杂，所以直接将环境光设置为一个常数，假设任何一点接受到的都是一个相同的环境光。

环境光不用考虑光的方向，与观察的方向也无关。

Blinn - Phong 模型的最终效果

将三种光照效果加在一起，就能够得到最终的光照效果，这看起来像是一个塑料。

着色频率（Shading Frequencies）

看一下下面的图中着色效果的差异：

左图能够明显的看到一个个四边形 ，中间的球的效果就平滑一些，右边的图更平滑一些。

这是因为三个球的着色频率不同，下面一一介绍三种不同的着色方式：

Flat Shading（左球）

这种着色方式可以明显的看出球表面上的三角形，感觉到球上面有许多棱角，在球上的着色并不平滑。

这种着色方法，是在一个三角形上取一个点进行着色，将这个点作为该面的着色（一个面上着色一次），在三角形的内部并不会发生颜色的变化，所以可以明显的看到球上的每个三角形。

Gouraud shading（中球）

这个球明显比上面的球要平滑许多，不能够清楚的看见球上的三角形了。

这种着色方法，是在每个三角形的顶点上进行一次着色，然后三角形内部的颜色为三个顶点的插值，这样三角形内部的颜色就会有一个渐变的效果，也能够更加平滑。

Phong shading（右球）

在每一个像素上都可以求得一个独特的法向量，然后就可以在每一个像素上都进行一次着色，这样就可以得到一个相对比较好的结果。

这种方法是在每一个像素上都进行一次着色。

着色频率的比较：面着色、点着色和像素着色

从上面的图可以看出，并不能简单的说哪种着色效果更好，着色的频率取决于面、点或者像素出现的频率，如果面的频率出现很高的话，那么用flat shading也是可以达到一个平滑的效果，如上图中最后一行。如果使用flat shading就能达到一个不错的效果，那么如果使用Phong shading的话就会增加额外的计算量，效率上就会降低 。

定义逐顶点的法线（Defining Per-Vertex Normal Vectors）

比如要找一个球上的顶点的法线，根据几何知识我们知道圆心和球面上点的连线就是该点的法线。但是我们并不总是使用球，如果我们使用其他的物体该怎么球法线呢？

因为每一个物体都是由许多三角形相连无缝贴合组成的，所以每一个顶点就会和许多不同的三角形有所关联，即一个顶点就是多个三角形的顶点，所以我们就认为这个顶点的法线就是周围相邻的几个面的法线的平均。

但是简单的平均没有意义，比如说一个三角形的面积很小，而另一个三角形的面积很大，那么这个大的三角形的法向量平均的份就应该多一些，相反，小三角形的法向量占平均的份就应该少一些。所以在平均时，将每个三角形的面积作为权值，对每个法向量进行加权平均，并且在求平均时要对向量进行标准化。

定义逐像素的法线（Defining Per-Pixel Normal Vectors）

比如说在三角形的内部我已经知道每一个顶点的法线是什么了，如何得到内部一个平滑过渡的法线？

给出顶点的法线，如何插值出中间的法线？这里就需要用到重心坐标，重心坐标等到后面再说。

图形（实时）渲染管线（Graphics(Real-time) Rendering Pipeline）

从场景到最后屏幕上显示的图，在这中间经历了什么样的过程，这个过程就是管线。其实表示的是一系列不同的操作，过程如下：

• 首先输入了1，2，3，4四个顶点的数据
• Vertex Processing : 经过变换、投影等操作，将这些点投影到屏幕上。
• Triangle Processing : 投影到屏幕上的一个个点都是离散的，将其连接起来，成为三角形
• Rasterization : 形成三角形之后要将三角形画在屏幕上，屏幕是由一个个像素组成的，是离散的，所以要经过光栅化将三角形离散成一个个像素（这里fragment是opengl中的概念，片段的意思，在这里我们就把它理解成像素）
• Fragment Processing : 对每个像素进行着色
• Framebuffer Operations : 得到屏幕上最终显示出来的图像

具体一下，每一步做的操作如下：

对模型的每一个顶点的位置进行变换。

光栅化，进行采样