本系列为慕课网《深度学习之神经网络(CNN/RNN/GAN)算法原理+实战》视频笔记，希望自己能通过分享笔记的形式更好的掌握该部分内容。
往期回顾：
神经网络（一）—— 机器学习、深度学习简介
神经网络（二）—— 神经元、Logistic回归模型

多分类的Logistic回归模型

多个神经元就可以得到多个输出！由此，我们可以得到多分类的Logistic回归模型。

• $W$从向量扩展为矩阵
• 输出$W\ast x$则变成向量
  
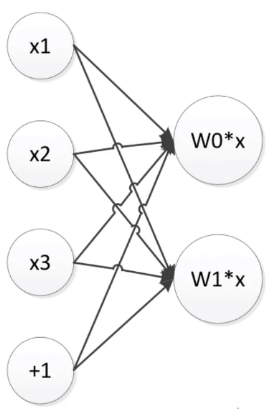
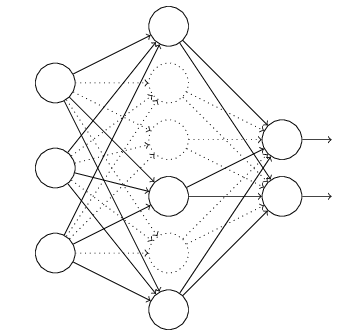
  上图为两个神经元组成的三分类模型，每个神经元有不同的权重$W$。

Example：

$X=[3,1,2]$，$W=[[0.4,0.6,0.5],[0.3,0.2,0.1]]$，
then, $Y=[y_0,y_1]=[W[0]\ast x,W[1]\ast x]=[2.8,1.3]$

多输出神经元$\to$softmax$\to$多分类Logistic回归模型

前一节（神经元、Logistic回归模型）我们已经学过了二分类Logistic回归模型通过sigmoid函数给出分类概率。但我们还可以换一个角度，把它看成将$1$和$e^{-w^{T}x}$做归一化。

对于$K$个分类的分类问题，如下图所示，$W$为一个$K-1$行的矩阵，将$K-1$个值和$1$一起做归一化，给出$K$个类别的分类概率。

具体地分类概率：
$$P(Y=k|x)=h_w(x)=\frac{e^{-w_k^{T}x}}{1+{\Sigma }_1^{k-1}{e}^{-w_k^{T}x}},k=1,2,...,K-1$$
$$P(Y=k|x)=1-h_w(x)=\frac{1}{1+{\Sigma }_1^{k-1}{e}^{-w_k^{T}x}},k=K$$

Example:

$Y=[y_0,y_1]=[2.8,1.3]$
$e^{-Y}=[e^{-2.8},e^{-1.3}]=[0.06,0.27]$
$Sum=1+0.06+0.27=1.33$
$P(Y=0|x)=0.06/1.33=0.045$
$P(Y=1|x)=0.27/1.33=0.203$
$P(Y=2|x)=1.00/1.33=0.752$
从Logistic回归模型的介绍，我们可以看出其实我们也可以把Logistic回归模型看成神经网络，多分类的Logistic回归模型已经有多个神经元了。

目标函数（损失函数）

• 衡量对数据的拟合程度。

Example：

$(x_1,y_1)=([10,3,9,20,...,4],1)$
$y_1^{\prime }=Model(x_1)=0.8$
$Loss=|y_1-y_1^{\prime }|=0.2$

One More Example:

$(x_1,y_1)=([10,3,9,20,...,4],3)$
$y_1^{\prime }=Model(x_1)=[0.1,0.2,0.25,0.4,0.05]$
$Loss=|y_1-y_1^{\prime }|=abs([0,0,0,1,0]-y_1^{\prime })=[0.1,0.2,0.25,0.6,0.05]=1.2$

常用目标函数

• 平方差函数
  $$\frac{1}{n}\Sigma \frac{1}{2}(y-Model(x){)}^2$$
• 交叉熵函数
  $$\frac{1}{n}\Sigma yln(Model(x))$$

神经网络训练

• 调整参数使模型在训练集上的损失函数最小