本文是跟着李沐老师的论文精度系列进行GNN的学习的，详细链接请见：零基础多图详解图神经网络（GNN/GCN）【论文精读】

该论文的标题为《A Gentle Introduction to Graph Neural Networks》，是对GNN的简介。那么论文的第一张图呢把鼠标放上去某一个结点将会表示出该节点的生成过程，可以看到放于Layer1中的某个节点时，它是由Layer2中的多个节点生成，而Layer2中的这些结点又有Layer3的部分节点生成，因此只要层次够深，那么一个节点就可以处理原始大片节点的信息。

图这种数据结构在当前随处可见，因此图神经网络如果能够发挥对图这种结构的良好处理能力，将会有很广泛的应用场景，例如药物的生成、车流量检测、推荐系统、人物关系等等。

文章的主要内容分为四块，分别是

• 什么样的数据结构可以表示为图
• 图和别的数据结构的区别在哪，为什么要用图神经网络
• 构建一个GNN查看内部各模块的内容
• 提供一个GNN的操作平台

1、什么是图

图实际上就是表示实体（顶点）的信息以及它们之间的连接关系（边）。而图的节点所包含的信息、边表达的信息、以及整个图表达的信息都可以用向量来表示。因此就存在三种向量。

而图又分为有向图和无向图，如下：

那么数据如何表示为图呢？

1.1 图片表示为图

如果将每个像素点看成一个顶点，而邻接的关系看成图中的边的，那么就可以用邻接矩阵来表示这个图像了，如下：

在图中我们可以看到，最左边的图呢代表每个像素它的位置，两位数字分别代表行和列，那么它旁边的那些像素总共有8个和它靠近，那么在第三张图中就有8的顶点和它存在边的连接。而如何将第三张图表示成数据呢，就是用邻接矩阵，可以看到邻接矩阵的行和列每个元素都是一个顶点，如果顶点和顶点之间存在边的关系那么将会在矩阵的对应位置用蓝色的点进行标注。因此我们就将图片表示成了一个图，再用邻接矩阵这种结构来表示图了。

1.2 文本表示为图

文本可以看成一个序列，将每个单词看成一个顶点，而相邻的单词可以看成存在有向边的连接，再用邻接矩阵来表示，如下：

1.3 其他数据结构表示为图

例如咖啡因分子：

人物关系图：

空手道道馆中老师与学生的关系图：

等等。

1.4、数据表示成图后存在哪些问题

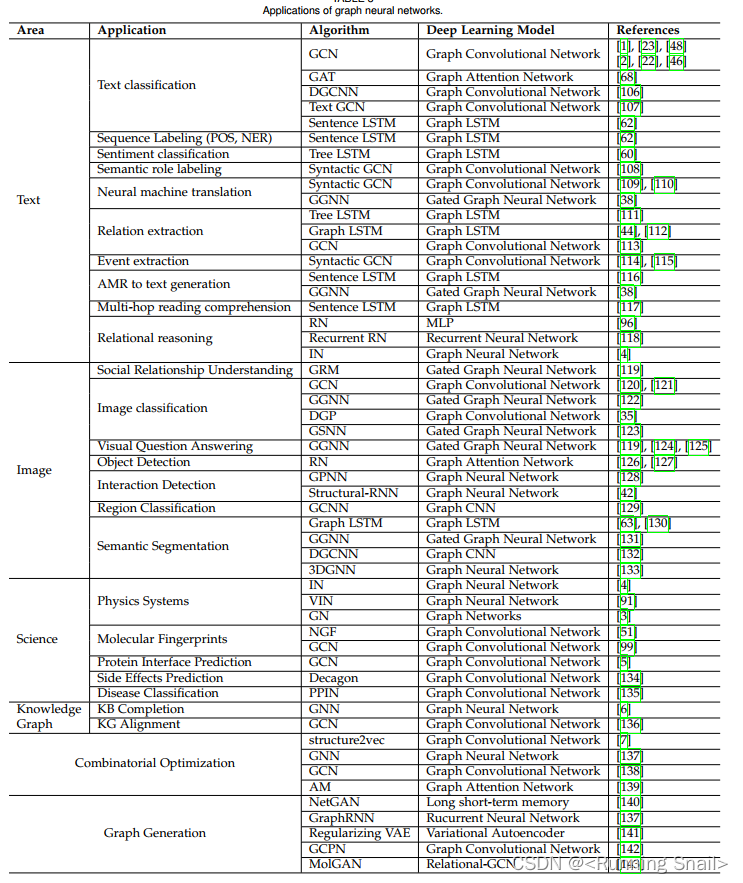
图上的问题大致上可以分为三类，第一类是关于整个图的任务，第二类是关于图中的顶点的任务，第三类任务是关于图中的边的任务。

• 关于整个图的任务

  例如我们将分子的结构表示成图之后，我们要识别该图中是否有两个环，那么我们就可以做成一个分类任务：

• 关于顶点的属性判断的任务

  对顶点进行划分，划分成两类，例如上述提到的空手道老师的任务，两位老师因为意见不合而决裂，那么我们所有的学生都要做出选择哪位老师的任务，因此就是对顶点的类型进行分类的任务：

• 关于边的属性判断的任务

  例如在下图中，先对各种元素进行提取成顶点，然后判断各个顶点之间是什么关系，例如观看、攻击等等：

也就是对一个图中的边的属性进行划分：

1.5、将机器学习用于图模型中将会有什么挑战

首先，前面说到的图的信息、顶点的信息、边的信息可以用向量来表示，这对于神经网络是由友好的。但是关于各个顶点之间的连接性应该怎么表达是一个大问题。而我们前面提到邻接矩阵，首先它所占用的空间会非常大，其次对于这种稀疏矩阵的高效处理也是一个很大的问题，再者如果我们将矩阵中的某些列或者某些行进行交换，是不会影响邻接矩阵所表示的含义的，如下图：

或者看下面这个例子，对于四个顶点的图可以有这么多可能的邻接矩阵：

这就需要我们保证我们的网络也能够在应对这样的变化时做出相同的决策。

那么我们可以用到如下这种数据结构来表示：

对于每个顶点和每条边，我们都可以用标量或者向量来表示它们的内部属性，全局的图也是一样的。而对于所有的连接信息，我们则可以维护一个连接列表的结构，其中每一个值代表每条边对应连接的两个节点。

2、图神经网络（GNN）

原文中对于GNN的定义是：

A GNN is an optimizable transformation on all attributes of the graph (nodes, edges, global-context) that preserves graph symmetries (permutation invariances)

意思就是GNN 是对图的所有属性（节点、边、全局上下文）的可优化转换，它保留了图的对称性（置换不变性），也就是将顺序变化之后不会影响的。而这里用到的神经网络结构为message passing neural network，即信息传递神经网络，它会对图中的各种属性向量进行转换，但不会改变其连接性。并且其输入和输出都是一个图。

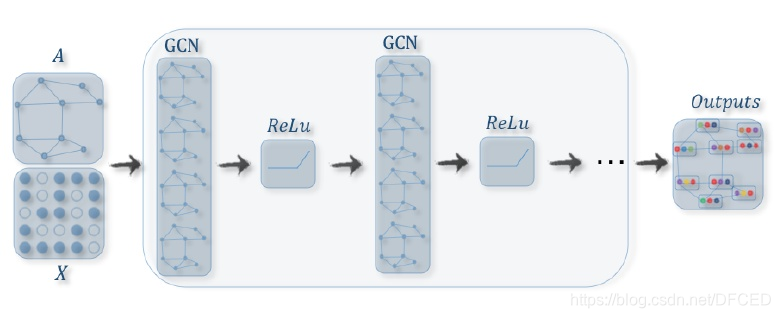
2.1 最简单的GNN

一个最简单的GNN如上图所示：对于图、顶点、边这三类属性分类构造一个多层感知机（MLP），然后将对应的向量输入进去后得到一个新的向量来表示新的信息。而这并不会改变原来连接性的信息，因此图的结构仍然是保持不变的。那么我们如何将这些信息转换成我们想要的输出呢

假设现在是对顶点的信息进行预测，就是之前空手道的二分类任务，那么我们可以在最后一层输出的图后，接上一个全连接层，然后再接上一个Softmax层即可，例如我们要进行二分类任务，那我们的全连接层的输出维度设为2即可，n分类就设为n。 需要注意的是不管有多少个顶点，它们是共享一个全连接层的，共享其中的参数。那么也就是所有的顶点共享一个全连接层，所有的边共享一个全连接层， 全局自己就拥有一个全连接层。

那么再来看稍微复杂一点的情况，例如某个顶点我们没有其向量该怎么办呢，可以采用pooling技术，即将与该顶点相连的边的向量和全局的向量进行相加，就得到了代表这个顶点的向量，那么我们就可以拿这个向量去做预测等任务了，示意图如下：

其中红色的箭头代表四条边的向量，蓝色箭头的向量代表全局的向量，那么相加就可以得到该顶点的向量了，可表示成下面的示意图：

那么如果有顶点的向量而没有边的向量也是同理，只需要将该边所连接的两个顶点的向量和全局的向量进行相加即可，即：

而如果是拥有顶点的向量而没有全局的向量，那么可以将全部顶点的向量加起来作为全局的向量，即：

所以不管缺乏哪一类的属性都可以通过pooling来补齐。

因此完整的最简单的GNN如下图：

但这部分的问题是在GNN blocks中并没有考虑到图的结构信息，这相当于对信息的浪费，结构可能不太理想。那么要用到下面的技术。

2.2 在图表的各部分之间传递信息

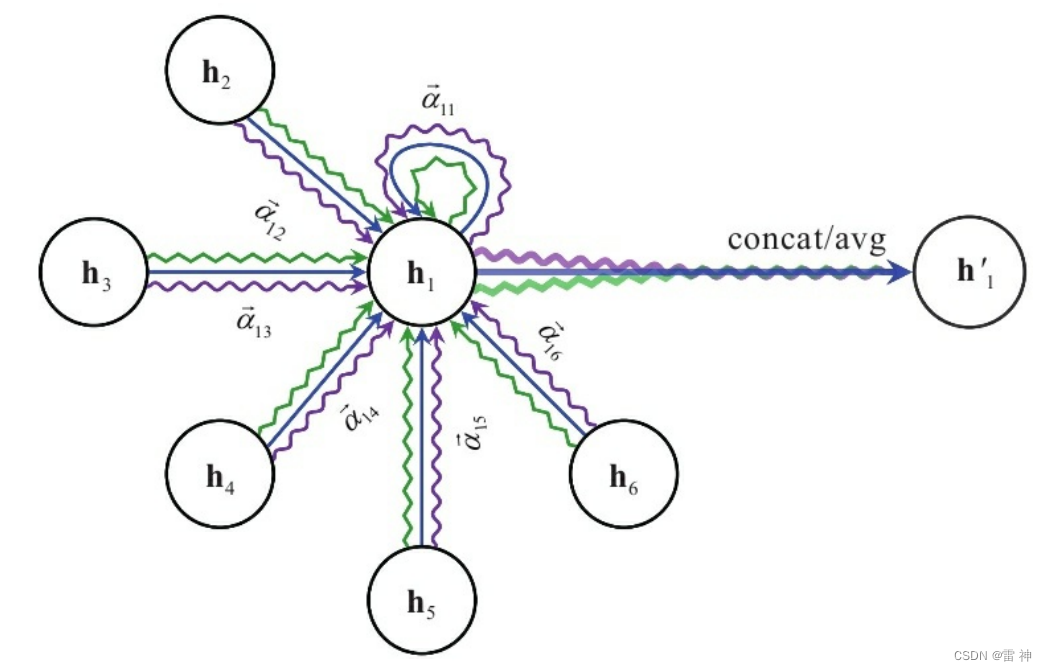
这部分的思想其实很容易理解，例如在对顶点进行更新时并不是直接进入MLP之中，而是将该顶点的向量和与之相连的所有顶点的向量求和，再进入MLP之中得到该顶点的更新向量，即：

这种情况呢就是只在顶点之间进行信息传递，即：

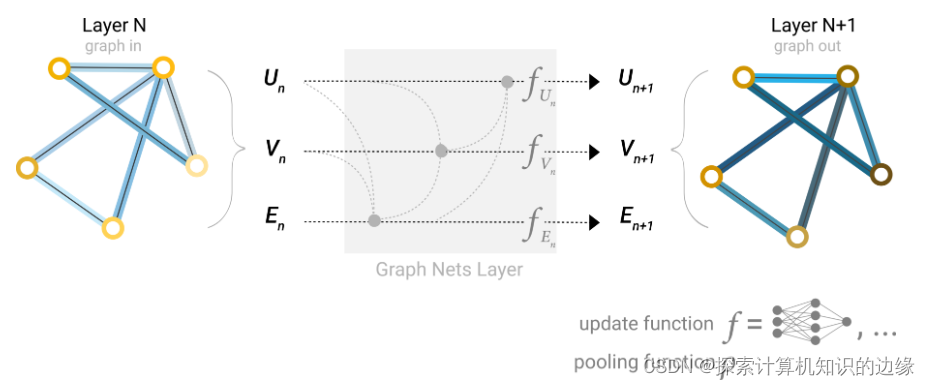
我们还可以实现更复杂的信息传递，例如把顶点的信息传递给边，把边的信息传递给顶点，即下图：

其中${\rho }_{V_n-E_n}$代表将顶点的信息传递到边，即将边相连的两个顶点的向量加到边的向量之上，而${\rho }_{E_n-V_n}$就是将边的信息传递到顶底，即将顶点有关系的边的向量都加到顶点的向量之上。完成之后再进入各自的MLP进行更新。这里需要注意的是这两个顺序交换是不一样的，即下面两种处理方式是不一样的：

但目前也没有特别明显的证明哪一种更好。另外一个办法就是两边同时更新，两种方式同时实施，即：

其实从之前我们就没有深入讲解说为什么需要一个全局的向量。这是因为如果你的图很大，有很多的节点但是连接又不够紧密的话，那么消息从一个顶点传递到远处的顶点可能需要很久的时间或者说很多次的传递过程，那么便虚拟化一个顶点，可以称为master node，该点呢与所有的顶点都相连，同时与所有的边都相连，作为消息传递的重要部分。那么对于全局向量加入了信息传递的过程就可以表示为下图，其中更新边的信息的时候是顶点和全局都传递信息，更新顶点的信息的时候是边和全局都传递信息，而同样，更新全局信息的时候也边和顶点都传递信息。

前述的pooling操作不仅仅可以求和，还可以做平均、取最大值这类操作。

3、当前技术综述

图除了我们前述的那种结构之外，是存在许多种其他结构的，例如下面这两种：

第一种是具有多种的边的类型，存在有向边和无向边；而第二种呢代表图可能是多层的，即当前层的某一个顶点其实可能是一整个图。

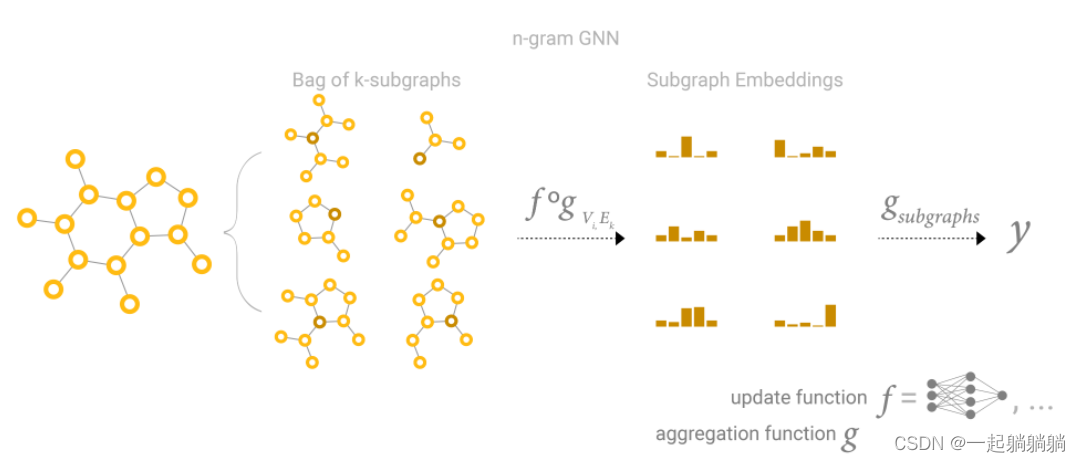
另外一个需要注意的点在于，如果层数较多那么后面层中的某一个顶点可能记录的信息就是整个图的信息了，那么求梯度的时候会非常复杂，因此可以尝试的方法是每次进行采样，采样得到一个子图然后再该子图上进行消息传递。