篇章二、vagrant中安装centos-7
前言
使用Vagrant创建镜像时,需要指定一个镜像,也就是box,若不存在Vagrant则会先从网上下载,而后缓存在本地目录下。
Vagrant有一个 镜像网站 ,可以根据需要在这个网站中下载所需镜像。
1、下载Centos7镜像
Centos的镜像下载网站是:http://cloud.centos.org/centos/
笔者需要的是Centos7镜像文件,因此直接上链接:
http://cloud.centos.org/centos/7/vagrant/x86_64/images/CentOS-7.box
2、添加box
下载完镜像文件后,需要将下载后的.box文件添加到vagrant中。
由于vagrant没有GUI操作页面,所以只能通过命令行操作。
# 1、查看box列表 --由于没有安装,所以这里会显示
# There are no installed boxes! Use `vagrant box add` to add some.
vagrant box list
# 2、将刚下载的box添加到vagrant中
vagrant box add D:\vagrant\download\CentOS-7.box --name centos-7
# 3、再次查看box列表 --这里就可以查看到了
vagrant box list
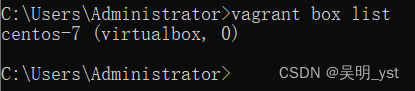
添加完box后,下一步便是安装Centos虚拟机。
3、安装Centos7虚拟机
首先创建虚拟机待安装目录下,并在当前文件目录下进入cmd。

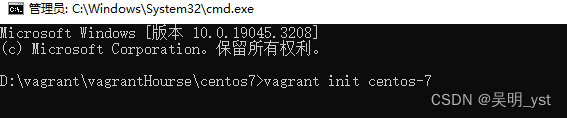
# 新建虚拟机,这里是centos-7则是box的名字
vagrant init centos-7
4、vagrant基本命令
# 1、启动虚拟机
vagrant up# 2、查看虚拟机状态
vagrant status# 3、停止虚机
vagrant halt# 4、暂停虚机
vagrant suspend# 5、恢复虚机
vagrant resume# 6、重载虚机
vagrant reload
这里需要强调vagrant up命令
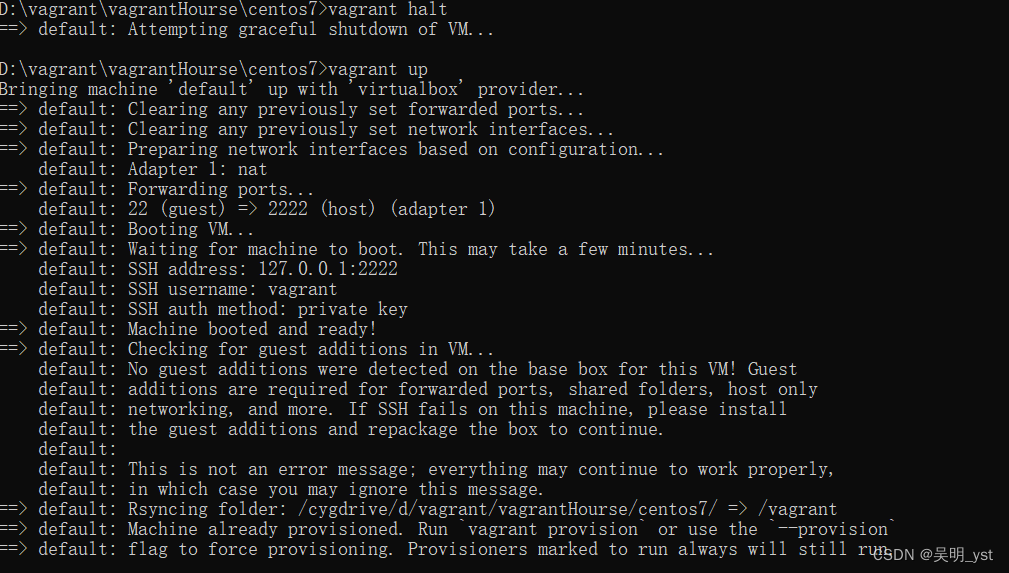
注意这些包含的信息:
网卡: Adapter 1: nat,第一块网卡,NAT 模式,这是固定的
端口转发: 22 (guest) => 2222 (host) (adapter 1),把虚机的 22 端口,映射到宿主机的2222 端口上,这样就可以通过 127.0.0.1:2222 访问虚拟机了
SSH用户名: vagrant,这里使用 private key 登录。密码也是 vagrant,但是密码方式仅供直接登录,是不能通过 SSH 登录的。
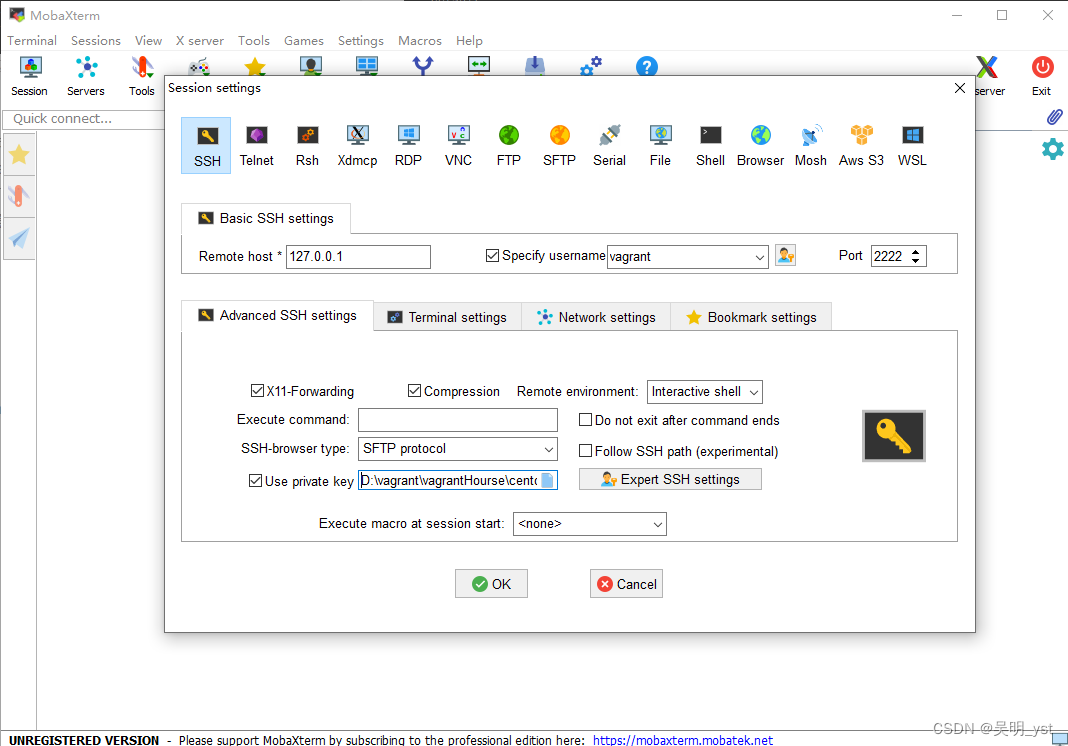
5、远程连接
这里要提及上文下载安装的MobaXterm远程连接工具。
在新建虚拟机后会在对应的文件夹下生成一个秘钥文件,如下方文件路劲:
D:\vagrant\vagrantHourse\centos7.vagrant\machines\default\virtualbox\private_key
输入远程地址、用户名、端口号(2222)、秘钥文件后即可成功连接。