目录

希尔排序

概念

算法思路

动画演示

代码如下

复杂度分析

时间复杂度测试

运行结果

 完整代码

 创作不易，如果本篇博客对您有一定的帮助，大家记得留言+点赞哦。

---

希尔排序

概念

希尔排序是插入排序的一种，是对直接插入排序的优化。其特点在于分组排序。

算法思路

希尔排序是按照其设计者希尔的名字命名的，他对插入排序的效率进行了分析，得出如下结论：

        1.在最坏情况下即待排序序列为逆序时，需要消耗O(n^2)的时间
        2.在最好情况下即待排序序列为顺序时，需要消耗O(n)的时间

于是希尔就想：若是能先将待排序序列进行一次预排序，使待排序序列接近有序，然后再对该序列进行一次插入排序。因此此时直接插入排序的时间复杂度为O(n)，那么只需控制预排序阶段的时间复杂度小于O(n^2)那么整体的时间复杂度就比插入排序的时间复杂度低了。

那具体的预排序应该怎么做才会时间复杂度满足要求呢？

        1.先选定一个小于n的整数gap（一般情况下是将n/2作为gap）作为第一增量，然后将所有距离为gap的元素分为一组，并对每一组进行插入排序
        2.重复步骤1，直到gap等于1停止，这时整个序列被分到了一组，进行一次直接插入排序，排序完成

你可能会疑惑，为什么gap由大到小？

因为gap越大，数据挪动的越快，耗时少；gap越小，数据挪动的越慢，耗时多。前期让gap较大，可以让数据快速移动到自己对应位置附近，减少挪动次数。

动画演示

 

我们来举一个实例：

 

首先gap取5，此时相隔距离为5的元素分到了一组（一共五组，每组两个元素），然后对每一组分别进行插入排序

 

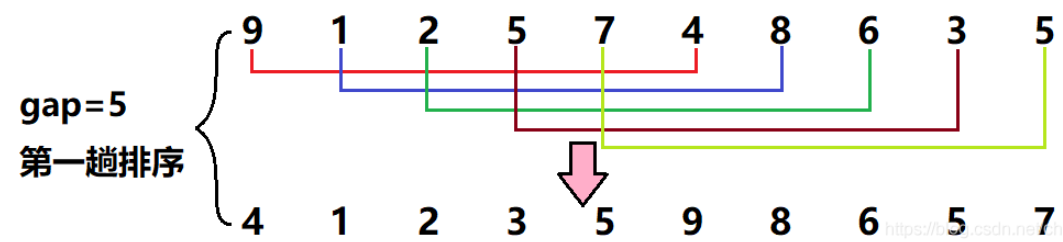
gap折半为2，此时相隔距离为2的元素被分到了一组（一共两组，每组五个元素），然后对每一组分别进行插入排序

 

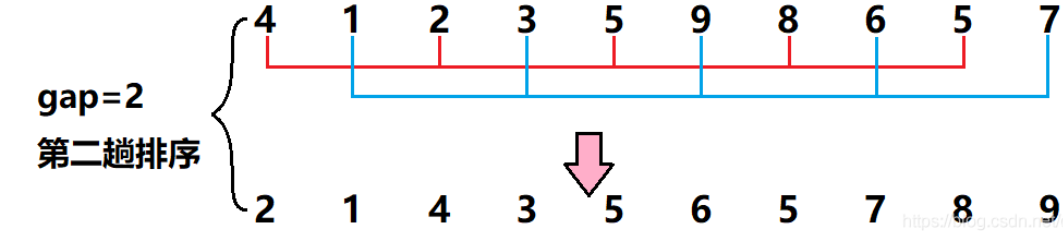
gap再次折半为1，此时所有元素被分到了一组，对它进行插入排序，至此插入排序完成

 

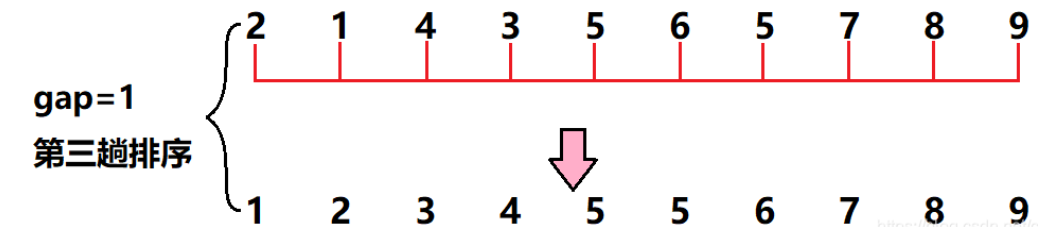
本例中前两趟就是希尔排序的预排序，最后一趟就是希尔排序的插入排序
 

代码如下

public static void shellSort(int[] a){int gal = a.length;while(gal>1) {int j = 0;gal/=2;   //特别之处gal  分组排序 5 3 1.。。//核心for (int i = gal; i < a.length; i++) {j = i-gal;if(a[j] > a[i]) {int tmp = a[j];a[j] = a[i];a[i] = tmp;}}}}

复杂度分析

 

 《数据结构-用面向对象方法与C++描述》--- 殷人昆

     时间复杂度  n^1.3 -- n^1.5  说不准  与每次分组的个数gap有关
     空间复杂度 O(1)
     稳定性 不稳定 当有几个相同的数字时，排序后相对位置会改变

时间复杂度测试

接下来我们试着用大量数据测试一下。

int[] a = new int[10_0000];  //10万个数据测试

1.orderArray函数实现生成一个基本有序数列，即从小到大排列。

public static void orderArray(int[] a) {for (int i = 0; i < a.length; i++) {a[i] = i;}}

2.notOrderArray函数生成一个倒序数列，即从大到小排列。

public static void notOrderArray(int[] a) {for (int i = 0; i < a.length; i++) {a[i] = a.length-i;}}

3.randomArray函数生成一个随机无序数列。

 public static void randomArray(int[] a) {Random random = new Random();for (int i = 0; i < a.length; i++) {a[i] = random.nextInt(10_0000);}}

4.testInsertSort函数测试   System.currentTimeMillis() 返回值单位是毫秒。

 

 public static void testInsertSort(int[] a){int[] tmpArray = Arrays.copyOf(a,a.length);long startTime = System.currentTimeMillis();    //注意用long接收shellSort(tmpArray);long endTime = System.currentTimeMillis();  //返回单位是毫秒System.out.println("直接插入排序耗时："+(endTime-startTime));}

5.main函数调用执行

public static void main(String[] args) {int[] a = new int[10_0000];//有序System.out.println("基本有序数列");orderArray(a);testInsertSort(a);//倒序System.out.println("逆序数列");notOrderArray(a);testInsertSort(a);//随机乱序System.out.println("无序数列");randomArray(a);testInsertSort(a);}

运行结果

         

 希尔排序和直接插入排序都属于插入排序，而希尔排序更是直接插入排序的优化。对比上文直接插入排序的测试结果。

            

 可以看出，希尔排序确实快了许多。并且耗时稳定。

 完整代码

import java.util.Random;public class sort {public static void main(String[] args) {int[] a = new int[10_0000];//有序System.out.println("基本有序数列");orderArray(a);testInsertSort(a);//无序System.out.println("逆序数列");notOrderArray(a);testInsertSort(a);//乱序System.out.println("无序数列");randomArray(a);testInsertSort(a);}//希尔排序  是插入排序的优化//时间复杂度  n^1.3 -- n^1.5  说不准  与每次分组的个数有关//空间复杂度 O(1)//稳定性 不稳定 当有几个相同的数字时，排序后相对位置会改变public static void shellSort(int[] a){int gal = a.length;while(gal>1) {int j = 0;gal/=2;   //特别之处gal  分组排序 5 3 1.。。//核心for (int i = gal; i < a.length; i++) {j = i-gal;if(a[j] > a[i]) {int tmp = a[j];a[j] = a[i];a[i] = tmp;}}}}//生成有序数组  从小到大排列public static void orderArray(int[] a) {for (int i = 0; i < a.length; i++) {a[i] = i;}}//n无序 其实就是从大到小排列public static void notOrderArray(int[] a) {for (int i = 0; i < a.length; i++) {a[i] = a.length-i;}}//乱序 随机生成序列public static void randomArray(int[] a) {Random random = new Random();for (int i = 0; i < a.length; i++) {a[i] = random.nextInt(10_0000);}}//大量数据测试public static void testInsertSort(int[] a){int[] tmpArray = Arrays.copyOf(a,a.length);long startTime = System.currentTimeMillis();    //注意用long接收shellSort(tmpArray);long endTime = System.currentTimeMillis();System.out.println("希尔排序耗时："+(endTime-startTime));}}

 创作不易，如果本篇博客对您有一定的帮助，大家记得留言+点赞哦。