目录

1. 引言

2. 为什么要使用索引？

3. 索引的概述

4. 索引的优点是什么？

4.1 降低数据库的IO成本，提高数据查找效率

4.2 保证数据库每一行数据的唯一性

4.3 加速表与表之间的连接

4.4 减少查询中分组与排序的执行时间

 5. 索引的缺点是什么？

5.1 创建索引和维护索引非常耗费时间

5.2 索引也是占用磁盘空间的

5.3 索引会降低表的更新速度

6. B+ 树到底是什么样的？

7. 数据库底层存储数据的实质

8. 索引的实现原理

9. 为什么B+树的高度不建议超过四层？

10. 什么是聚簇索引？

10.1 聚簇索引的特点

10.2 聚簇索引的优点？

10.3 聚簇索引的缺点？

10.4 聚簇索引的补充说明

11. 什么是非聚簇索引？

12. 什么是回表？

13. 为什么非聚簇索引的叶子节点不存储一份完整的数据方便查找呢？

14. 聚簇索引与非聚簇索引的区别？

15. 什么是联合索引？

---

1. 引言

我们知道，只要谈起数据库，索引重中之重，不管你是面试开发程序员，架构师，甚至是校园招聘，你会发现几乎都问到了索引。那么它到底是个什么东西？竟能如此重要。它到底有什么好处呢？为什么面试的时候总喜欢问索引呢？它的底层实现是什么样的呢？今天我们就一同来揭晓这些问题的答案。

提前声明，想要更加透彻深入的学会索引，建议你对数据结构有很好的了解，特别是树和链表，如果你对树这种结构很清晰，那么学会索引非常轻松，如果不会，也没关系，并没有很大影响。

2. 为什么要使用索引？

想要理解索引，我们首先要知道为什么要使用索引。

我来说一个场景，假设现在我的一张用户表中有十万条用户数据，用户 id 唯一，我想要查询id 位80000的用户信息，那么数据库是靠什么快速的在十万条数据中找到这条id为80000的用户数据的呢？各位有没有想过这个问题？

其实底层就是索引在帮忙，做一个简单的比喻，如果我们把刚才的用户表中的数据存放到一本字典中，那么索引就是这个字典的目录，当我们想要查找某一个数据的时候，数据库底层不会傻乎乎的去一页一页从字典中翻找我们想要的数据，而是直接去翻这根本字典的目录，通过目录精准定位我们想要查询的数据在哪一页，然后直接定位到那一页，将我们要查找的数据取出。

那么各位再想一下，如果字典没有目录。会是什么样的结果呢？我们要查找用户张三的信息，然后数据库受到了指令，从第一页开始翻看查阅，没有翻到第二页，有没有翻到第三页......各位想过没有，这会多麻烦，所以，通过字典目录提高查找效率是必须要做的，通过索引查找数据也是迫在眉睫的，但同样，我们既然制造了目录，如果我们对字典中的数据做了更改，目录是不是也要改啊，这就为我们后续索引的缺点做了铺垫。

总结来说就一句话，之所以要使用索引，是因为索引可以提高我们查找数据的效率。

3. 索引的概述

MySQL官方给索引的定义是：索引(Index)是帮助MySQL高效获取数据的数据结构。

简洁点来说，索引的本质是数据结构。

此外，索引是在存储引擎中实现的，当我们的存储引擎不同时，索引底层的数据结构也不相同。

同时，存储引擎中还定义了一个表中最多不能超过16个索引，但其实我们也用不到这么多，所以完全可以放心；也定义了索引的长度不能超过256个字节，其实也很大了，我们通常不会把索引定义那么大，也可以放心。

4. 索引的优点是什么？

4.1 降低数据库的IO成本，提高数据查找效率

各位细想，我们的数据都是存储在磁盘上的，只有我们在需要的时候才会从磁盘IO读取到内存中。那么用户表的那本字典，如果没有索引，我会就会先从磁盘IO加载第一页的数据到内存，然后遍历数据，发现没有找到，再经过IO磁盘，加载第二页的数据到内存，再遍历查找...... 各位知道，内存中数据的处理速度是很快的，但是从磁盘加载到内存这个速度就很慢了，假设我们遍历一页数据需要1ms，那么IO一次可能就需要50ms，这还只是加载了第一页的数据，那如果有很多很多页数据，查找速率绝对非常慢。但是如果我们使用了索引，我们只需要IO一次将索引加载到内存中，遍历索引，精准找到数据所在的页数，然后第二次IO直接读取是数据所在的那一页数据，这样的话，只需要经过两次磁盘IO就可以得到我们需要的数据了。

4.2 保证数据库每一行数据的唯一性

我们知道，表中通常都是有主见的，而且都会设置为非空且唯一，我们的索引也是一样，索引也是具有唯一性的，通过创建唯一索引，可以保证数据库表中每一行数据的唯一性。

4.3 加速表与表之间的连接

对于有父子关系的子表与父表在进行联合查询时，索引可以加速表与表之间的连接，从而提高表的查询效率。

4.4 减少查询中分组与排序的执行时间

各位想一下，字典中的目录我们都是按照一定的规律去进行排列的，索引也是一样的道理，从小到大把数据进行排列，既然是已经排好序的数据了，当我们在查询语句中对数据进行ORDER BY 排序时候，其实已经是有序的了，那么就省去了我们再次排序的时间，而且以后查询排序都不需要浪费时间，是一个一劳永逸的做法。

 5. 索引的缺点是什么？

5.1 创建索引和维护索引非常耗费时间

这一点我想不难理解，各位想，当我们对一本书中的内容做了更改之后，你是不是也要去更改目录啊，特别是你的书内容如果不较多，如果你删除了几页内容，其他的内容都要跟着做调整；如果你一直往书中继续写内容，目录也要跟着增多吧，所以说，索引的创建与维护也是非常浪费时间的。

5.2 索引也是占用磁盘空间的

则会就好比是一本书，你书中的内容需要用纸张去些内容，那么目录也要写在纸上啊；而且索引本身就是数据结构，是需要占用磁盘的空间的，并且随着你数据量的增大，你索引所占的磁盘空间大小很有可能会超过数据本身所占的磁盘文件大小。

5.3 索引会降低表的更新速度

其实这一点与维护索引是有一些内在关联的，如果我们对表中的数据做了动态修改，那么索引也是会不断地去动态修改维护的，这就大大的降低了表的更新速度。

6. B+ 树到底是什么样的？

我们知道，数据结构中有一种数据结构叫做树，我们最常见的就是二叉树，还是平衡二叉树，还有二叉树的升级版红黑树。

既然有二叉树，就有三叉树，N叉树。

其实，B+树底层就是一个N叉树，这里我以三叉树为例，模型如下图所示

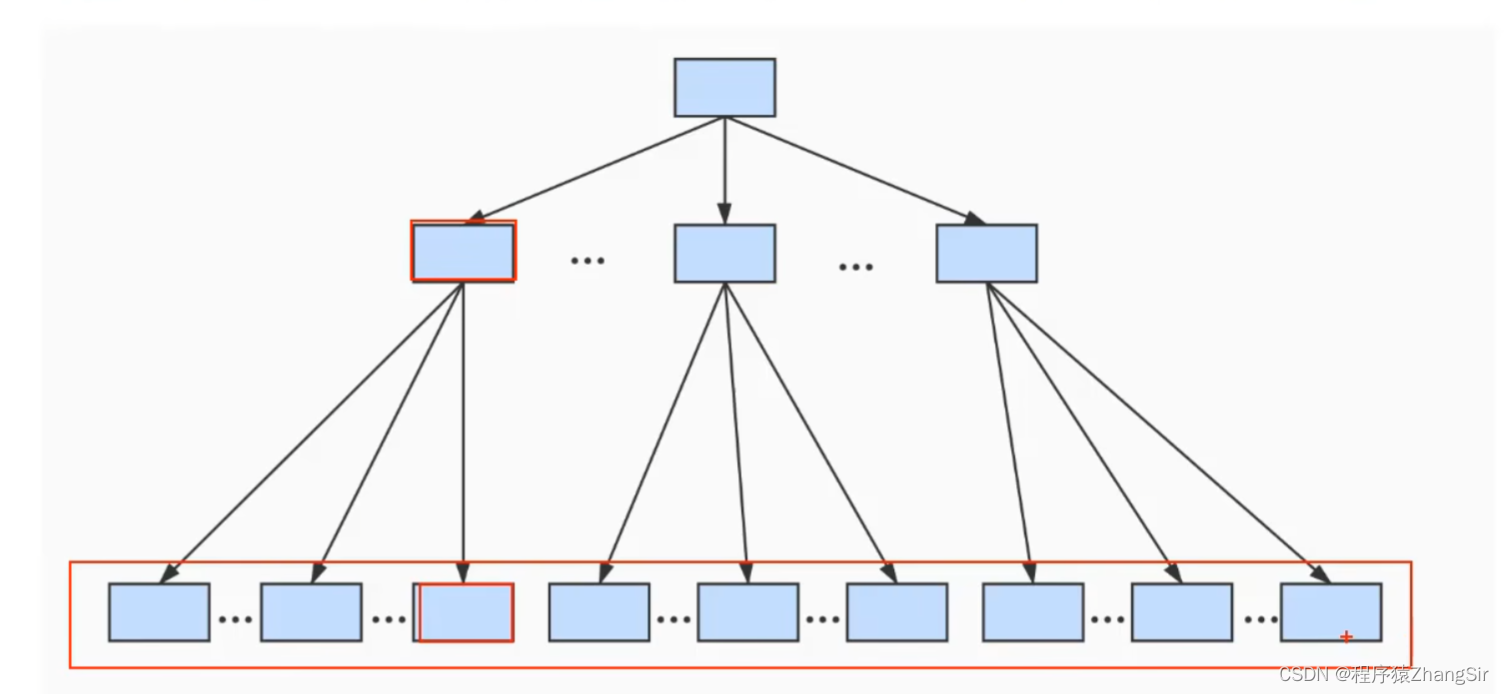
我们的对顶层就是根节点，中间层是子节点，最下层是叶子节点。

在数据库底层 InnoDB 存储引擎中，存储数据和索引就是采用B+树的形式存储的。

7. 数据库底层存储数据的实质

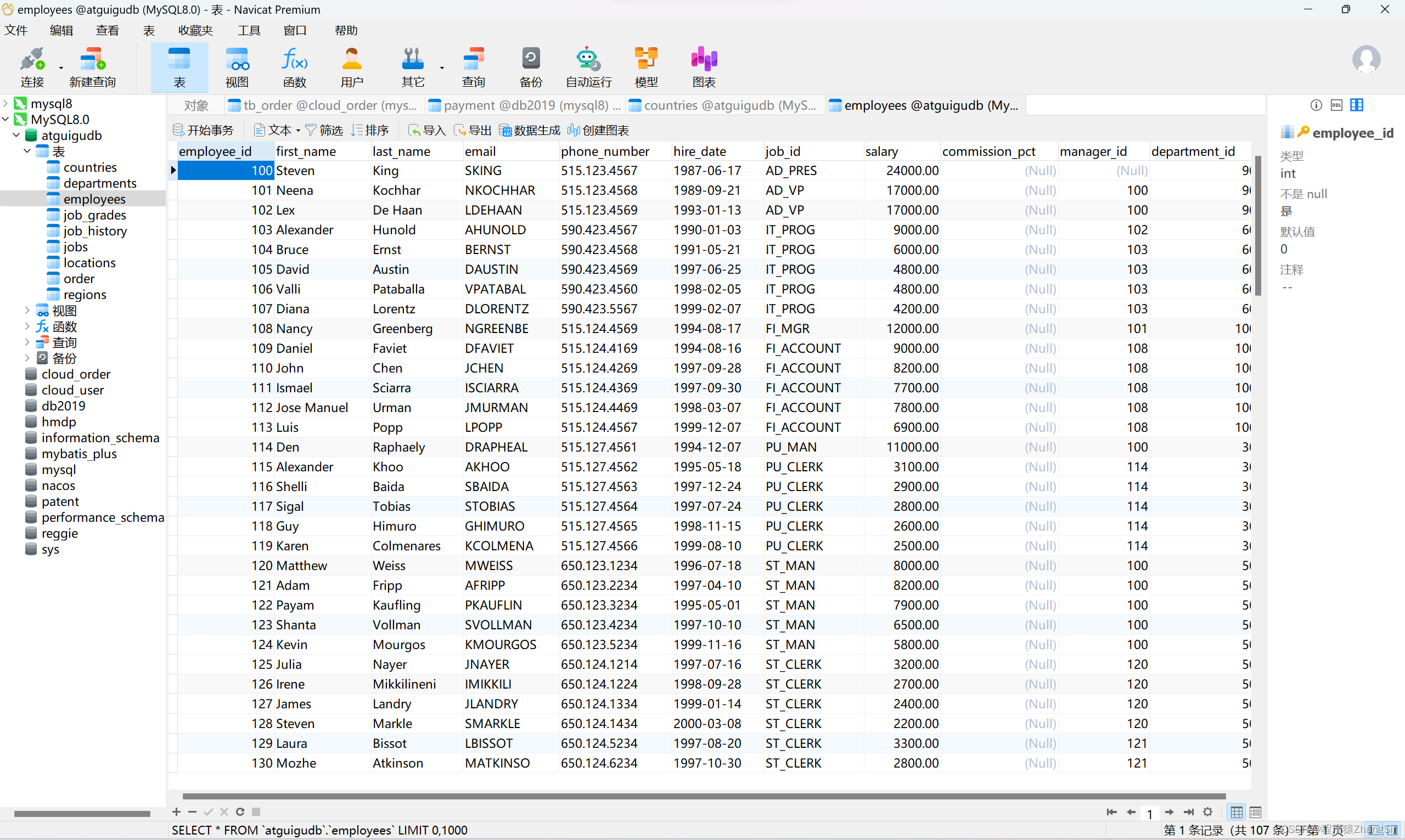
如上图所示，是我们数据库中常见的一张表，这里有很多的数据，但是在底层，你们知道吗，表的每一行数据都是单独存储的，在磁盘上的存储位置是不连续的。因为如果我们表中的数据有很多，达到了上万条数据，那么在磁盘中不一定有那么大的一个连续空间，因此在数据库底层，它的每一行数据都是单独存储的，而且还要满足一个逻辑上的连续，我们 employee_id = 100 的员工下一条记录是 employee_id = 101 的员工这一点是不能变的，不能说我查一次，它们的顺序就变一次，一定要它们保持一定的逻辑连续性。

说到这里各位应该就明白了吧，没错！就是链表，其实表中的每一行数据在磁盘底层是采用单向链表的形式来存储的，这样不仅解决了存储空间大小不够问题，还解决了让它们在逻辑上满足连续性的问题。

就拿上面这张表举例，在数据库的底层，employee_id = 100 的员工就是链表的头节点，它内部还会存储 employee_id = 101 的员工的地址值，从而找到该员工的全部相关信息，而employee_id = 101 的员工内部也会存储 employee_id = 102 的员工的地址值，通过该地址值找到 employee_id = 102 的员工全部信息由此形成一个单向链表。

8. 索引的实现原理

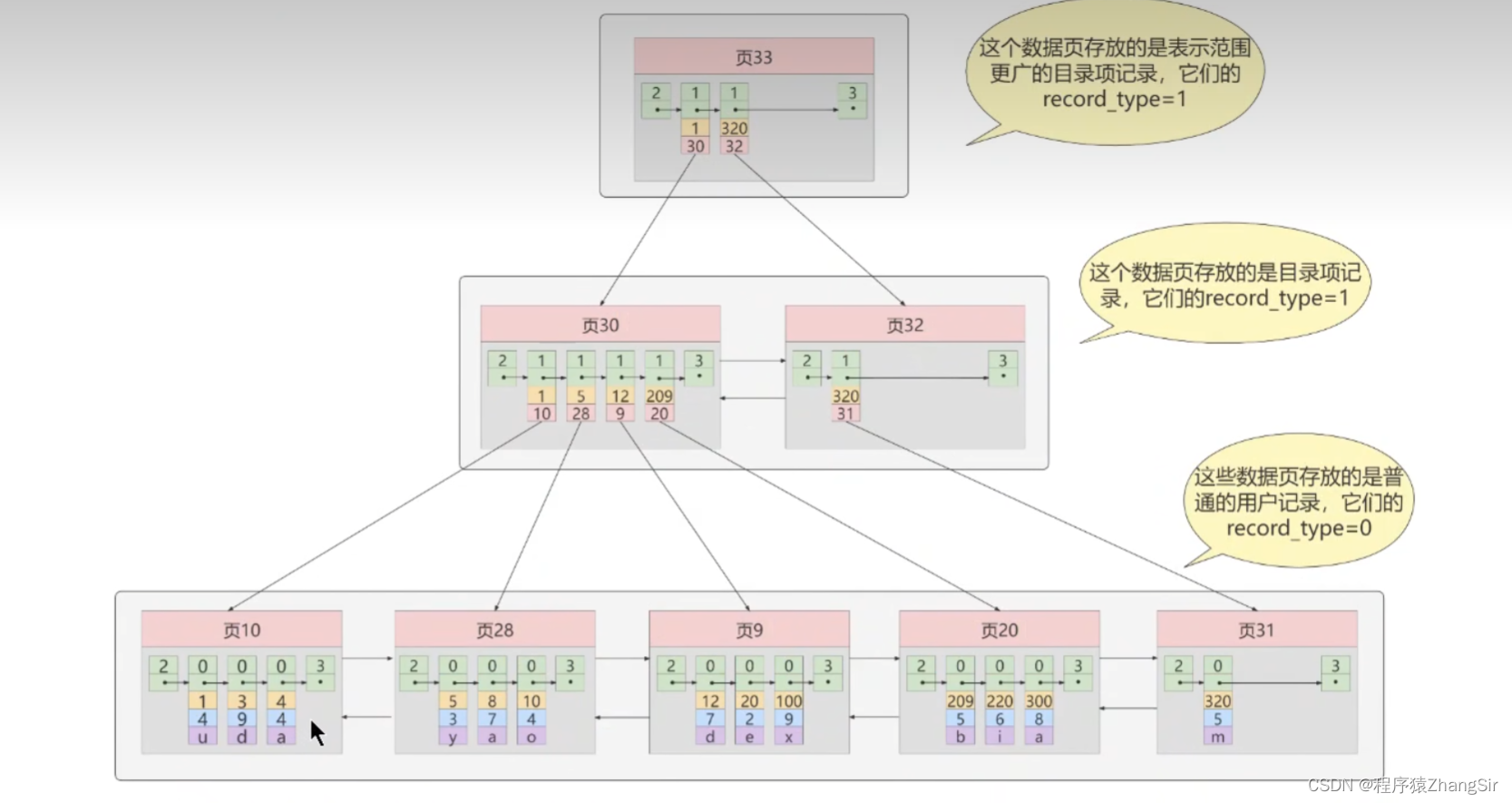
如上图，根据上面B+树的结构，我们就能大致推演出索引的底层原理了，这里我化繁为简，简单说明。

我们先看最下层，最下层也是叶子节点页，这些叶子节点页之间是使用双向链表进行连接的，而内部的数据则是我刚刚说的通过单向链表连接的，图中已经标识出，而且每一页中都有一个数组，存放主键的值，方便我们后续使用二分法快速确定要查找的数据。在B+树索引中，所有的真实数据都是存放在叶子节点叶中的，如图，在叶子节点中页10中，下方的 1，4，u；3，9，d；4，4，a 就是一条条真实的数据，上方的0就是指这些是数据，假设1，3，4这些首字段为一条条数据的主键。

我们继续推演，如果没有中间层页30与页32，只有最下方一层，当我们想要找想要查找主键为100的用户信息时，就需要从页10开始从头遍历这个双向链表，在遍历到页9的时候，找到了主键为100的用户，我们直接获取到该用户的信息，一共遍历了3页，需要进行三次磁盘IO。

如果我们加上中间层，为每一个叶子节点页再创建一个目录，即页30与页32，页30下方存储了1，10；5，28；12，9；209，20四条数据。这里的1，10中的1指代的就是叶子节点页10中最小的一条数据1，10则是指代页10，实际存储的是页10的内存地址；5，28则是叶子节点页28中的最小主键值5与该页所在的地址值，这些数据上方都是1，表示他们仍然是目录页而不是真实的数据...... 我们使用了这个中间目录页之后，我们再去获取主键为100的用户数据时，就会先去遍历中间页，在中间页中确定主键值为100的用户数据存放在页9中，就可以直接将页9中的数据全部读取到内存，然后再去寻找该用户的数据，可以发现，此时加上了中间页之后，只需要两次IO，节约了时间，提高了查找效率。

我们继续类比推理，如果以后我的数据越来越多，中间也最多只能存放四个叶子节点页的数据，再多就存不下了，这个时候，我们就需要继续创建新的中间页，而如果中间页一直增多，就会面临和刚才叶子节点页一样的问题。

这个时候，我们就可以套娃式的去再创建一个中间页的顶层也，让这个顶层页使用类似的手段存放中间页的重要数据。举例说明，我们想要查找主键为300的用户数据，第一次磁盘IO，我们把页33的全部数据加载到内存中，经过二分查找判断发现与主键为300的用户数据应存放在子页30中，在然后进行第二次IO，将子夜30的全部数据加载到内存中，再经过二分查找判断，确定主键为300的用户数据存应放在叶子节点页20中，在进行第三次磁盘IO，将叶子节点页20中的数据全部加载到内存中，再经过二分查找，快速定位到主键为300的用户所在的内存地址，获取到信息，此时只需要经历三次磁盘IO，而且非常稳定，当我们想要查询某条数据是，都是进行三次磁盘IO就可以获取到结果，找得到或找不到都要返回，极大的保证了我们查找数据时的稳定性。

9. 为什么B+树的高度不建议超过四层？

在刚才我举得例子中，各位应该看得出来，我所举例的B+树是三层，绝大多数情况下都是三层，最多四层。而在面试的时候，有些面试官会问你为什么B+树的不建议超过四层，请给出具体的原因。

原因如下：

不知道各位发现了没有，当我们的B+树只有两层时，我们最多就可以经过两次磁盘IO就可以查找到数据，当B+树是三层时，我们进行三次磁盘IO就可以获取到数据。这也从侧面印证了一点，我们与磁盘交互的次数，是受到B+树高度的影响的，各位都知道，内存中处理数据速度是非常快的，二分查找数据可能就1ms~3ms左右的时间，而与磁盘IO就不一样了，磁盘IO一次可能就需要花费100ms，每交互一次100ms，这个效率是非常低的，因此我们应当尽量减少与磁盘的IO次数，这就要求我们B+树的高度不能过高，最好三层，不能超过四层。

那肯定会有人问，问什么非要是三层或四层，我选五层不行吗？

其实从原则上来讲也是可以的，但是我们还要考虑数据的存储量，这里给各位说一下，数据库的底层一个真实的数据页大小是16KB，也就是 16000 个字节，假设我们的每条数据占用160个字节，160个字节已经不小了，完全够用，那么我们每个叶子节点页就可以存储 16000/160 = 100 条数据。而我们的非叶子节点页，因为并没有存储真实的用户数据，所以可以存储更多的内容，假设我们的目录页可以存储 1000 条叶子节点页数据，当我们的B+树正好满两层的时候，存储的数据量是 100 * 1000 = 100,000 十万条数据；当我们 B+ 树满两层时，存储的数据量是 100 * 1000 * 1000 = 100,000,000 一亿条数据；让我们的B+树满5层时，存储的数据量是 100 * 1000 * 1000 * 1000 = 100,000,000,000 一千亿条数据，可以看到，当B+树5层的时候，数据量已经非常恐怖了，而且我们也不可能在一张表中存储这么多数据。

而在实际开发业务的时候，我们会采用微服务的架构，并对数据库进行分库分表，进行读写分离，不会让大量数据在同一张表中存储，既不安全，效率又低。因此，我们通常会把B+树控制在三层左右，此时一张表就足以存储一亿条数据，而且只需要三次磁盘IO就可以查找到想要的数据，综合考虑是最优的选择。如果像阿里京东腾讯这些用户量多余1亿的企业，也有可能会采用四层B+树，但其实还是是很少这么做的。这就是为什么要把B+树的高低控制在四层以下，总的来说就一句话，三层或四层B+树，既满足了数据量的存储需要，又达到了最佳查找效率。

10. 什么是聚簇索引？

聚簇索引，又名主键索引，它是基于表的主键而生成的索引，而且它不是一种索引的类型，而是一种数据的存储方式(表中所有的用户数据都会存放在叶子节点中)如下图所示就是一个经典的聚簇索引。在 InnoDB 引擎中，聚簇索引是不需要我们手动创建的，在我们创建好表结构的时候，数据库的底层已经为我们生成聚簇索引，并随着我们数据的添加，索引会一直不断的变化和维护。

10.1 聚簇索引的特点

聚簇索引还有一些特点，只有满足以下四点的索引才能称为聚簇索引：

1. 每个页内的记录是按照的主键的大小顺序形成的一个单向链表，例如页10中的（1，4，u）与（3，9，d）便是通过单向链表连接的；

2. 各个存放的数据页之间采用的是双向链表进行连接，如图中的页10与页28之间就是双向链表；

3. 存放目录项记录的页(即刚才我所提的中间层)它们之间也是采用双向链表的形式进行连接，如图中的页30与页32就是双向链表；

4. B+ 树中存放的是完整的表数据，如图中页10的（1，4，u），（3，9，d）等，这里我列的简单，只有三个字段，实际聚簇索引存储的数据会以你定义的表中的字段为主；

10.2 聚簇索引的优点？

（1）因为聚簇索引中将索引与所有的表数据都存储在了B+树种，所以聚簇索引比非聚簇索引查询效率要高；

（2）因为聚簇索引是基于主键大小排列的索引，所以对于主键的范围查找与排序查找速度非常快；

（3）因为聚簇索是引按照一定的顺序进行排列，再查询显示一定范围的数据的时候，由于数据是紧密相连的，数据库就不需要从不同的区块中去提取数据，节省了大量的IO操作。

10.3 聚簇索引的缺点？

（1）插入的速度严重依赖于插入的顺序。因为聚簇索引是按照逐渐的顺序去建立的，如果我们不按照顺序去插入，而是突然插入一个主键值大的数据，又突然插入一个主键值小的数据，这就会导致索引会不断地去动态变化，还可能出现页分裂，严重影响性能，因此对于 InnoDB 引擎来说，建议在插入数据的时候按照顺序插入或者使用主键自增策略。

（2）更新主键的代价极高。因为聚簇索引就是基于几件生成的，如果我们对主键做出更改，那么整个索引结构可能都要进行更改，而进行更改是非常耗费性能的，因此对于 InnoDB 引擎来说，我们一般最好把主键定义为不可更改。

10.4 聚簇索引的补充说明

（1）MySQL 数据库目前只有 InnoDB 引擎支持聚簇索引，MyISAM 引擎不支持聚簇索引；

（2）由于数据物理存储排序方式只有一种，所以每个 MySQL 表只能有一个聚簇索引，一般情况下都是该表的主键；

（3）如果我们没有给表定义主键，那么 InnoDB 会选择一个非空且唯一的字段替代，如果也没有这样的字段，那么 InnoDB 会隐世式定义一个主键作为聚簇索引；

（4）为了充分利用聚簇索引的特性， InnoDB 引擎下在定义表的主键的时候，不建议使用无序的id，例如UUID，MD5，HASH，字符串等作为主键，否则无法保证数据的顺序增长。

11. 什么是非聚簇索引？

非聚簇索引，也可以叫二级索引，或叫辅助索引。

刚才我们说到了，聚簇索引是 InnoDB 引擎基于主键自动生成的，可以提高有关主键的查找速度和查找范围，也就是说只有搜索条件中包含主键字段时才有效果。那么当我们不使用主键字段来查找数据而是基于普通字段查找数据同时又想提高查找效率的时候，我们就可以通过普通字段定义非聚簇索引。如下图所示就是一个非聚簇索引所构成的 B+ 树。

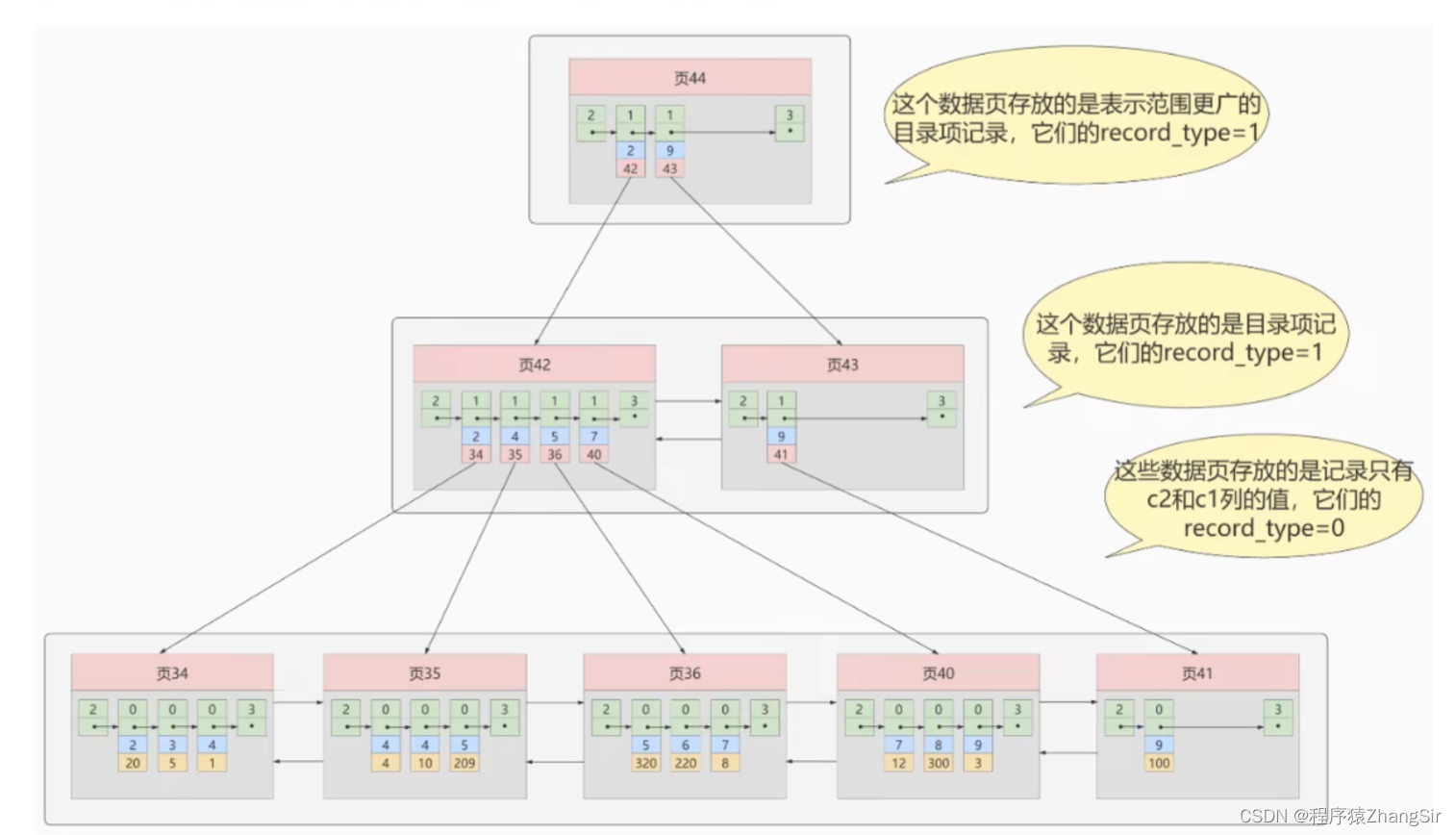
这里需要注意一点，非聚簇索引构成的 B+ 树与聚簇索引构成的 B+ 树稍有不同。

这里目录页44与子目录页42，43的原理与聚簇索引中类似，但叶子节点中就不一样了，刚才我说到了，聚簇索引中，存放着完整的表数据，而在非聚簇索引中，叶子节点中只存放着索引对应的那个普通字段与主键值。如图中，蓝色对应的就是普通字段，黄色对应的就是主键值，我们可以看一下，在前面那张图中，页9中存放这一条数据（20，2，e），正好对应着我们这里的非聚簇索引，这里页34下面蓝色方块中值为2的数据对应的主键值也为20，这样说各位同学应该更好理解一些，各位可以将上图与前面聚簇索引中的字段值做对比就可以看出来，我就不一一举例说明了。

12. 什么是回表？

刚才我说到了，在非聚簇索引中，叶子节点只存放了该索引字段的相关信息和主键信息，那么只有这两项信息肯定是不够的，如果我们的目的是通过非聚簇索引查询某条用户的全部信息，它就会进行回表操作，什么是回表呢？

其实很简单，当我们使用非聚簇索引的字段作为查询条件去查询表中的相关信息时，数据库会先根据非聚簇索引形成的 B+ 树，一步步查找到与查询条件相关的信息，再根据它们各自对应的主键去聚簇索引中查询完整的用户信息，这个过程中，需要先查询非聚簇索引的 B+ 树，再去查询聚簇索引的 B+ 树，查询之后又回去再查了一次表，这个过程就叫做回表。

举个栗子，现在有一张表 user ，主键 uid ，手机号码 phone，用户名 username，密码 password四个字段，我们给手机号码字段创建了非聚簇索引，那么它的底层就会只存储手机号码信息和所对应的主键uid 信息，当我们通过 手机号去查询用户完整信息时，语句应该是 SELECT * FROM user WHERE phone = "待查询用户手机号"；在这个查询语句中，它会先去非聚簇索引形成的 B+ 树通过 phone 查找到对应的主键uid，查找到主键uid的信息之后，它会再去聚簇索引的 B+ 树中通过 uid 查询出完整的用户信息并返回，这就是它在底层的执行逻辑，先查非聚簇索引，再回表查聚簇索引。

13. 为什么非聚簇索引的叶子节点不存储一份完整的数据方便查找呢？

这个问题其实也算是一个面试题。我刚才说了什么是回表，但是不知道各位发现一个问题没有，回表还需要再查寻一次 B+ 树，这样不是很麻烦吗？我们直接将用户的全部信息在非聚簇索引的 B+ 树中叶存储一份多省事啊，怎么不这样做呢？

如果你也有这样的问题，说明你认真思考了。大家想一想，在聚簇索引中，我们已经存储了一份完整的表数据，还有 B+ 树的结构，这些都是非常占用磁盘满空间的，而非聚簇索引又不止可以创建一个，我们可以创建多个，刚才我举的例子中只有四个字段，在实际的业务场景中，二十个字段也是很有可能的，如果我们为了方便查找又创建了三个非聚簇索引，并且图方便在非聚簇索引中也存储完整的用户数据，各位同学想一想，这样是不是非常冗余，我们的用户数据明明存储一份就够了，但是你创建一个非聚簇索引，数据就多存储一份，再创建一个，再存储一份，我们创建三个非聚簇索引，那么加上聚簇索引我们底层的数据足足存储了四份，非常非常冗余，这是绝对不允许的。另外，如果我们把全部的数据都存在非聚簇索引中，那么当我们要对用户数据作出修改时，有多少个索引，我们就要修改多少次，各位想是不是，我们对用户张三做修改，所有的索引中关于张三的信息都要做修改，非常不划算不值得。所以不在非聚簇索引上也存储一份完整的用户数据，一方面是为了防止数据大量冗余，造成磁盘资源的浪费；另一方面是防止多余的操作。

14. 聚簇索引与非聚簇索引的区别？

（1）聚簇索引叶子节点存储的是完整的用户数据，而非聚簇索引中存储的只有主键与索引字段数据，非聚簇索引不会影响表的物理存储结构；

（2）一个表只能有一个聚簇索引，但是可以有多个非聚簇索引；

（3）使用聚簇索引时，查询效率很高，但如果是对数据进行增删改操作，效率会比非聚簇索引低；

15. 什么是联合索引？

说的准确一些，联合索引其实属于是非聚簇索引中的一种，它与我们说的联合主键是有一些类似的，刚才我们说的非聚簇索引是使用一个字段构成 B+ 树，而有些时候我们会把数据库中的两个字段都作为索引，这种情况下形成的索引就叫联合索引。

举个例子，假设一张学生表 student ，有主键字段C1，非主键字段C2，C3，C4，C5。现在我们为C2与C3创建联合索引，那么形成的 B+ 树中就会存放 C2，C3，C1字段，并按照从上到下的顺序排列，会先比较联合字段C2的大小，先按C2大小排序，当C2大小相同时，再根据C3大小排序，在下方存贮主键C1的值，从而形成一个联合索引 B+ 树。