插入排序

像玩扑克牌摸牌时一样，一张一张摸，每摸到一张插入到对应的位置，插入排序就是从第一个位置开始，进行插入，每次插入之插入到前面的位置，直到排序完成。平均效率为O（n方）

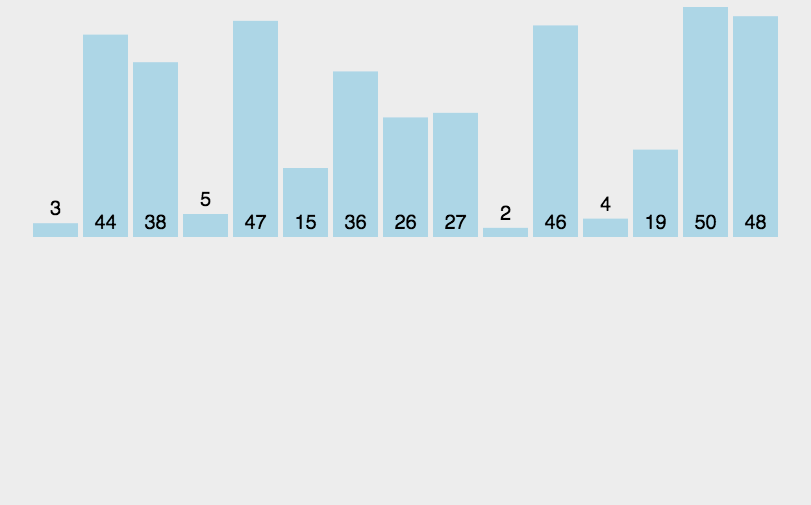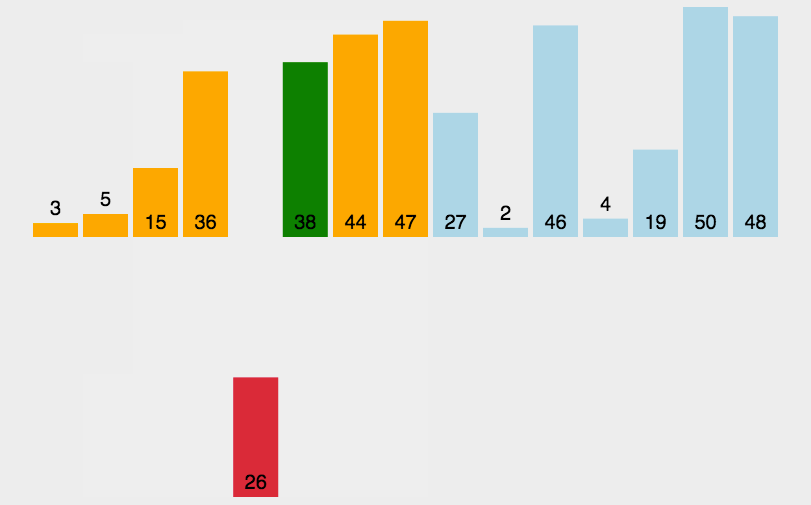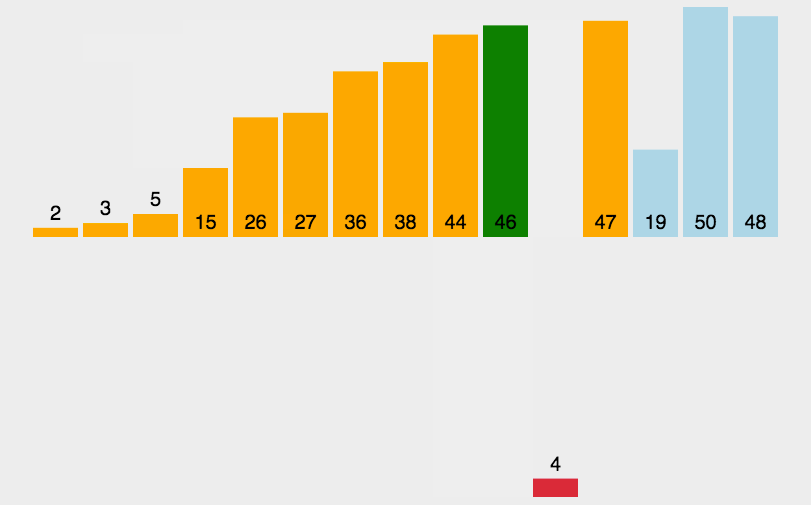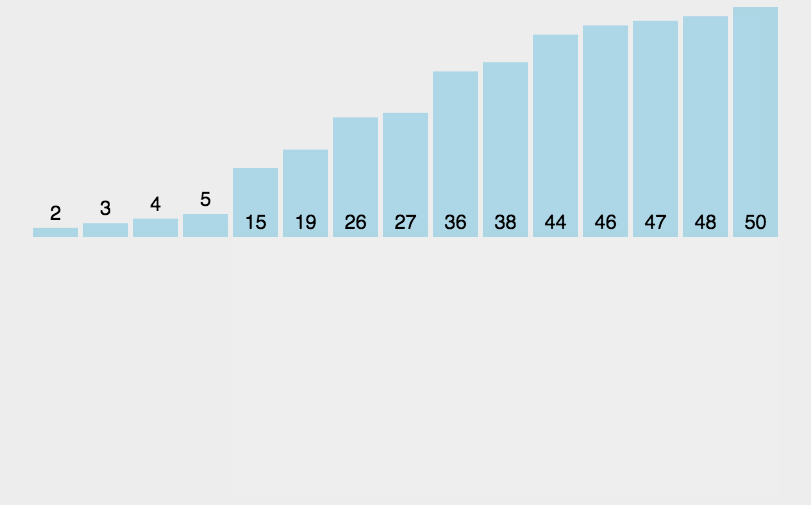
请添加图片描述

外层循环代表循环次数，end为准备插入牌的位置，依次向前比较，直到找到合适位置，temp为准备插入牌的值，内层循环依次对前面的值进行比较，直到找到合适位置停下。

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i + 1;int temp = a[end];while (end > 0 && temp < a[end - 1]){a[end] = a[end - 1];end--;}a[end] = temp;}
}int main()
{int a[] = { 6,4,8,2,1,4,9,7,5,3,21,4,8,5 ,3,5,6,3,2,3,4,56,34,2,2,2,4,5,56,5,43 };InsertSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}
}

希尔排序

希尔排序为插入排序的优化版本，平均效率为O（nlogn），在插入排序的基础上加一个分组，定义一个gap，间隔gap的为一组，这样可以让小的数据有更快的速度到达前面，省去了插入排序的一个一个比较，每组最小的数据都在前面，然后再所以gap，再次进行分组排序，直到剩下gap为1的时候，回归到插入排序，但是这时整个数组已经基本有序，只需要少量的交换即可。

请添加图片描述

void ShellSort(int* a, int n)
{int gap = 3;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i + gap;int temp = a[end];while (end > 0 && temp < a[end - gap]){a[end] = a[end - gap];end -= gap;}a[end] = temp;}}
}int main()
{int a[] = { 6,4,8,2,1,4,9,7,5,3,21,4,8,5 ,3,5,6,3,2,3,4,56,34,2,2,2,4,5,56,5,43 };ShellSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}}
}

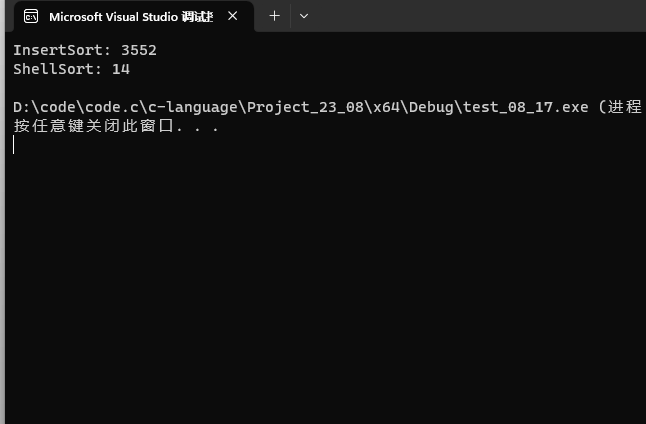
插入排序VS希尔排序测试

对二者速度测试之后得出结论，在数据越多的情况下，希尔排序就越高效。

void test()
{srand(time);int n = 100000;int* arr1 = (int*)malloc(sizeof(int) * n);int* arr2 = (int*)malloc(sizeof(int) * n);for (int i = 0; i < n; i++){arr1[i] = rand();arr2[i] = arr1[i];}int start1 = clock();InsertSort(arr1, n);int end1 = clock();int start2 = clock();ShellSort(arr2, n);int end2 = clock();printf("InsertSort: %d\n", end1 - start1);printf("ShellSort: %d\n", end2 - start2);
}int main()
{test();
}