数据结构：二叉树的递归实现(C实现)

在这里插入图片描述

个人主页 ： 个人主页
个人专栏 ： 《数据结构》 《C语言》

文章目录

  • 前言
  • 一、树的概念
  • 二、二叉树
    • 二叉树的概念
    • 二叉树的性质
  • 三、二叉树链式结构实现
    • 二叉树节点定义
    • 创建二叉树节点
    • 遍历二叉树
      • 先序遍历二叉树(BinaryTreePrevOrder)
      • 中序遍历二叉树(BinaryTreeInOrder)
      • 后序遍历二叉树(BinaryTreePostOrder)
      • 层序遍历二叉树(BinaryTreeLevelOrder)
    • 二叉树节点个数(BinaryTreeSize)
    • 二叉树第K层节点个数(BinaryTreeLevelKSize)
    • 二叉树叶子节点个数(BinaryTreeLeafSize)
    • 二叉树查找值为X的节点(BinaryTreeFind)
    • 判断二叉树是否是完全二叉树(BinaryTreeComplete)
    • 通过前序遍历的数组构建二叉树
  • 四、代码展示
    • 二叉树代码展示
    • 队列代码展示
  • 总结

前言

本篇博客主要讲解二叉树的相关操作如下：

//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);//二叉树的销毁
void BinaryTreeDestroy(BTNode* root);//二叉树节点个数
int BinaryTreeSize(BTNode* root);//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);//二叉树第K层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);//二叉树查找值为X的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);//二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);//二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);//二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);//层序遍历
void BinaryTreeLevelOrder(BTNode* root);//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x);

一、树的概念

树是一种非线性结构，它是由n个有限节点组成的一个有层次关系的集合。

在这里插入图片描述

  • 图中A节点没有前驱节点，被称为根节点
  • 除根节点外，其余节点被分成两个无不相交的集合T1(B,D,E,F…)，T2(C,G,H,L…)。其中每个集合T又是一颗结构与树类似的子树。每一颗子树的根节点有且只有一个根节点，可以有0个或多个后继节点
  • 因此，树是递归定义的。
  • 树的子树不能有交集，否则就为图。
  • 节点的度：一个节点含有的子树的个数称为该节点的度；如上图A节点的度是2
  • 叶节点或终端节点：度为0的节点被称为叶节点；如上图：K,J,F,L,O,P为叶节点
  • 非终端节点或分支节点：度不为0的节点；如上图：A,B,C,D,E…等节点为分支节点
  • 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点。如上图A节点是B,C的父节点
  • 孩子节点或子节点：若一个节点含有子树，则子树的根节点就是该节点的子节点。如上图B,C是A的子节点
  • 兄弟节点：具有相同的父节点的节点互为兄弟节点。如上图B,C互为兄弟节点
  • 树的度：一颗树中，最大节点的度就是该数的度。如上图数的度为3
  • 节点的层次：从根开始定义起，根为第一层，根的子节点为第二层，依次类推。如上图G节点的层次为3
  • 树的高度或深度：树中节点的最大层次。如上图树的深度为5
  • 堂兄弟节点：父节点在同一层的节点互为堂兄弟节点。如上图D,G互为堂兄弟节点
  • 节点的祖先：从根到该节点所经分支上的所以节点。如上图A是所以节点的祖先
  • 子孙节点 ：以某节点为根的子树中任一节点都称为该节点的子孙。如上图所以节点是A的子孙
  • 森林：由m棵互不相交的树的集合称为森林

二、二叉树

二叉树的概念

由一个根节点加上两颗子树构成 。

在这里插入图片描述

  • 二叉树的度最大为2
  • 二叉树是有序树，二叉树的子树有左右之分，次序不能颠倒

二叉树的性质

若规定根节点的层数是1，则一个非空二叉树的第K层最多有2^(k - 1)个节点

若规定根节点的层数是1，则深度为h的二叉树的最大节点数是2^h - 1

对于任何一颗二叉树，如果度为0的节点为N0，度为2的节点为N2，那么N0 = N2 + 1 (数学归纳)

若规定根节点的层数是1，具有N个节点的满二叉树的深度为log(n + 1)[以2为底]

对于具有n个节点的完全二叉树，如果按照从上至下从左到右的数组顺序对所以节点从0开始编号(也就是堆的结构)，则对序号为K的节点有：
若k>0,k节点的父节点的序号：(k - 1) / 2;
如果k是0(根节点)，则无父节点
若2k+1<n，左孩子序号 2k+1，右孩子序号2k+2 如果2k+1> n则无左孩子 2*k+2>n则无右孩子

三、二叉树链式结构实现

二叉树节点定义

节点需要一个数据域，一个指向左孩子节点的指针，一个指向右孩子节点的指针。
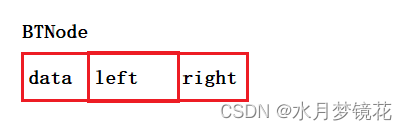
在这里插入图片描述

typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;

创建二叉树节点

我们只需要传递二叉树节点的数据即可，动态开辟出的节点空间用返回值的方式接受。
malloc出一块节点空间，将函数参数给data，使left 和 right 指向NULL，返回该空间的地址

在这里插入图片描述

//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x)
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc:");exit(-1);}root->data = x;root->left = root->right = NULL;return root;
}

为了方便我们理解，这里我们先手动创建一个二叉树来进行讲解相关操作，最后在来讲解先序创建二叉树。

void test()
{BTNode* a = BuyBinaryTreeNode('A');BTNode* b = BuyBinaryTreeNode('B');BTNode* c = BuyBinaryTreeNode('C');BTNode* d = BuyBinaryTreeNode('D');BTNode* e = BuyBinaryTreeNode('E');BTNode* f = BuyBinaryTreeNode('F');BTNode* g = BuyBinaryTreeNode('G');BTNode* h = BuyBinaryTreeNode('H');a->left = b;b->left = d;b->right = e;e->right = h;a->right = c;c->left = f;c->right = g;
}

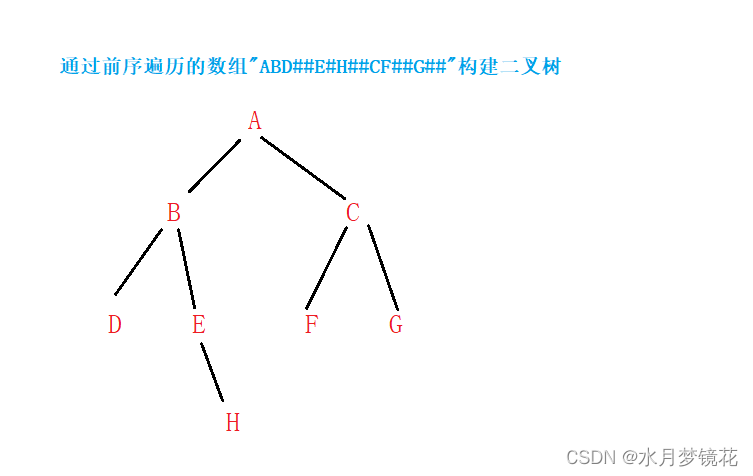
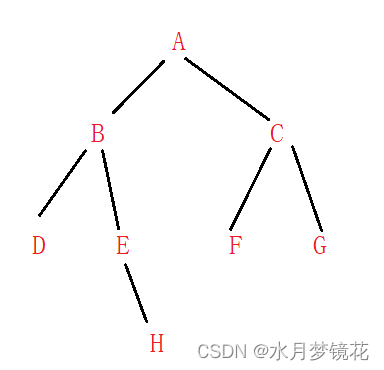
创建的二叉树就是下图所示：
在这里插入图片描述

遍历二叉树

遍历二叉树有多种方式：

  • 先序遍历 ：根节点 -> 左子树 -> 右子树
  • 中序遍历 ：左子树-> 根节点 -> 右子树
  • 后序遍历 ：左子树 -> 右子树 -> 根节点
  • 层序遍历 ： 从左到右从上到下，依次遍历二叉树节点

先序遍历二叉树(BinaryTreePrevOrder)

对于下图中的二叉树，其先序遍历结果为：ABD##E#H##CF##G##( ’ # ’ 表示NULL )
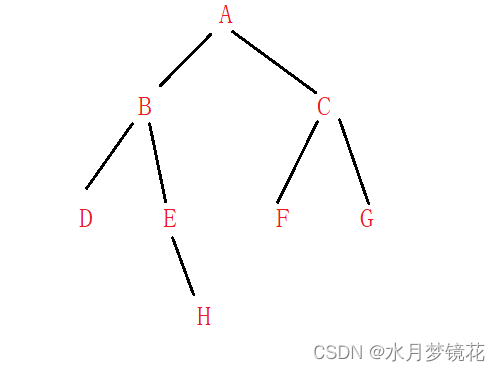
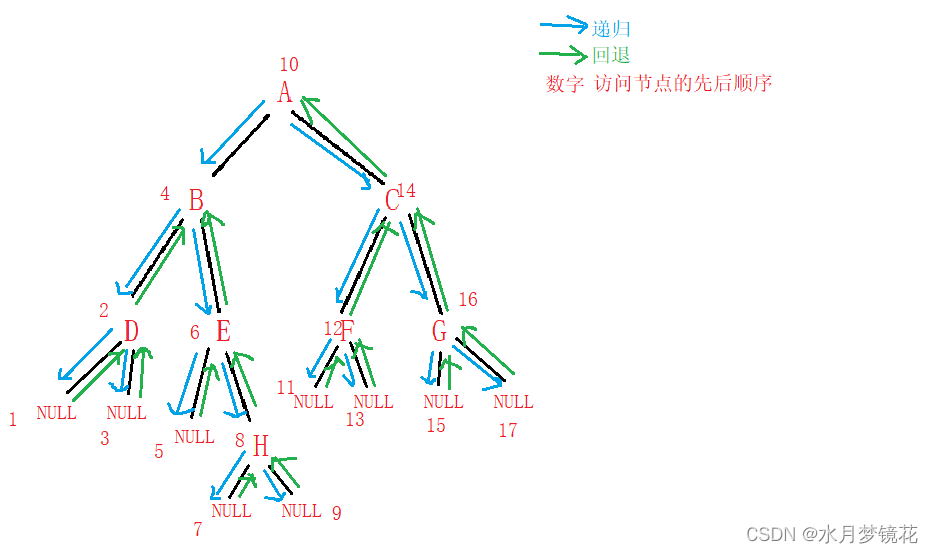
在这里插入图片描述
那么是如何遍历的？我们需要按照根，左，右的顺序递归二叉树即可。
在这里插入图片描述

//二叉树前序遍历   根节点 左子树  右子树
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//根节点printf("%c ", root->data);//左子树BinaryTreePrevOrder(root->left);//右子树BinaryTreePrevOrder(root->right);
}

这份代码是如何展开的？
在这里插入图片描述

中序遍历二叉树(BinaryTreeInOrder)

中序遍历与先序遍历类似，只有将根节点的访问与左子树递归交换执行顺序即可
对于下图中的二叉树，其中序遍历结果为：#D#B#E#H#A#F#C#G# ( ’ # ’ 表示NULL )
在这里插入图片描述
在这里插入图片描述

//二叉树中序遍历		左子树  根  右子树
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreeInOrder(root->left);//根printf("%c ", root->data);//右子树BinaryTreeInOrder(root->right);
}

后序遍历二叉树(BinaryTreePostOrder)

后序遍历，就是再次调整根节点的访问顺序，将根节点的访问顺序调整到左子树递归与右子树递归后即可。

对于下图中的二叉树，其中序遍历结果为：##D###HEB##F##GCA ( ’ # ’ 表示NULL )
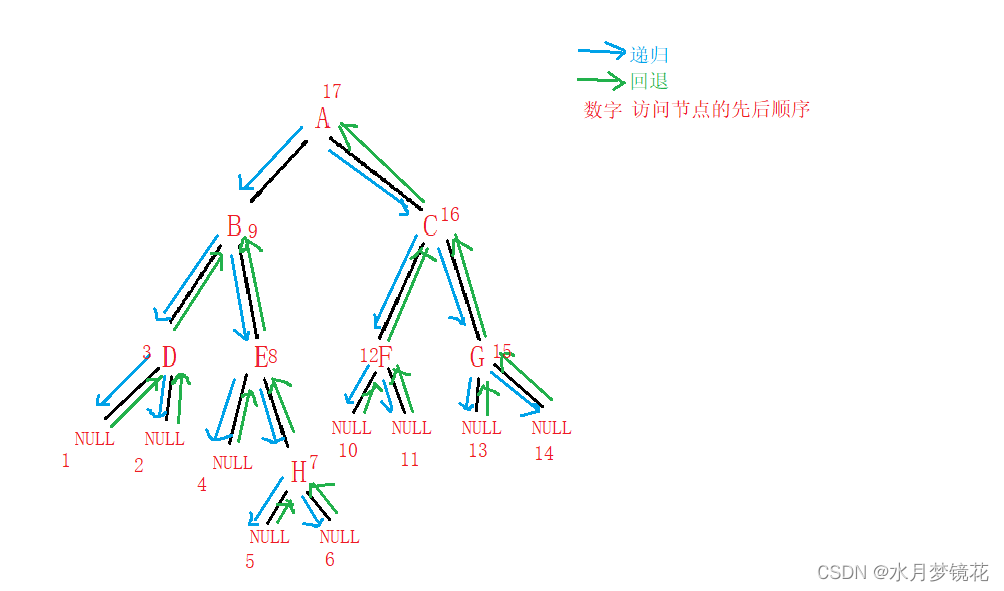
在这里插入图片描述
在这里插入图片描述

//二叉树后序遍历  左子树 右子树 根
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreePostOrder(root->left);//右子树BinaryTreePostOrder(root->right);//根printf("%c ", root->data);
}

层序遍历二叉树(BinaryTreeLevelOrder)

要实现二叉树的层序遍历，我们需要借助队列。
我们将根节点先入队列，之后我们每次出队头数据时，将该队头数据指向的左子节点 与 右子节点分别入队列，如果左子节点 或 右子节点 为NULL就不入队列，重复上述过程直到队列为空

在这里插入图片描述

//层序遍历  借助队列  出队头数据时，将其左子节点 与 右子节点依次入队列
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);//入根节点QuenePush(&q, root);//队列为空，代表二叉树中元素也遍历完成while (!QueneEmpty(&q)){QDataType val = QueneFront(&q);printf("%c ", val->data);//入数据  该节点的左节点 与 右节点if (val->left != NULL)QuenePush(&q, val->left);if (val->right != NULL)QuenePush(&q, val->right);//出队头数据QuenePop(&q);}QueneDestrory(&q);
}

二叉树节点个数(BinaryTreeSize)

我们使用递归的思路来看待二叉树节点个数的接口。
子问题：根节点的左子树的节点个数 与 根节点的右子树的节点个数
结束条件：空节点返回
所以求二叉树节点个数的问题可以转换为求根节点左子树节点数 + 根节点右子树节点数 +根节点的节点总数

//二叉树节点个数   根节点的左子树与右子树的节点个数和  
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}//        左子树节点数                 右子树节点数               根节点return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

对于下面二叉树的递归展开图：
在这里插入图片描述
在这里插入图片描述

二叉树第K层节点个数(BinaryTreeLevelKSize)

函数声明：

int BinaryTreeLevelKSize(BTNode* root, int k);

子问题：根节点左子树第K-1层节点个数 与 根节点右子树第K-1层节点个数
结束条件：访问到空节点 或 找到所求层数(k == 1)

也就是说，求二叉树第K层节点数的问题转换为求根节点左子树第K-1层节点数 与 根节点右子树第K-1层节点数之和。

//二叉树第K层节点个数       左子树的第k-1层节点数 + 右子树的第k-1层节点数     不同栈帧的k互不影响
int BinaryTreeLevelKSize(BTNode* root, int k)
{//如果 k 超过数的深度if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

对于下面二叉树，求第3层节点数的递归展开图。
在这里插入图片描述
在这里插入图片描述

二叉树叶子节点个数(BinaryTreeLeafSize)

函数声明：

int BinaryTreeLeafSize(BTNode* root);

子问题：根节点左子树叶子结点 与 根节点右子树叶子结点
结束条件：访问到空节点 或 访问到叶子结点

原问题转换成根节点左子树叶子结点个数 + 根节点右子树叶子结点个数。


//二叉树叶子节点个数   左子树的叶子节点 + 右子树的叶子结点
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

对于下面二叉树，求其叶子结点的个树的递归展开图
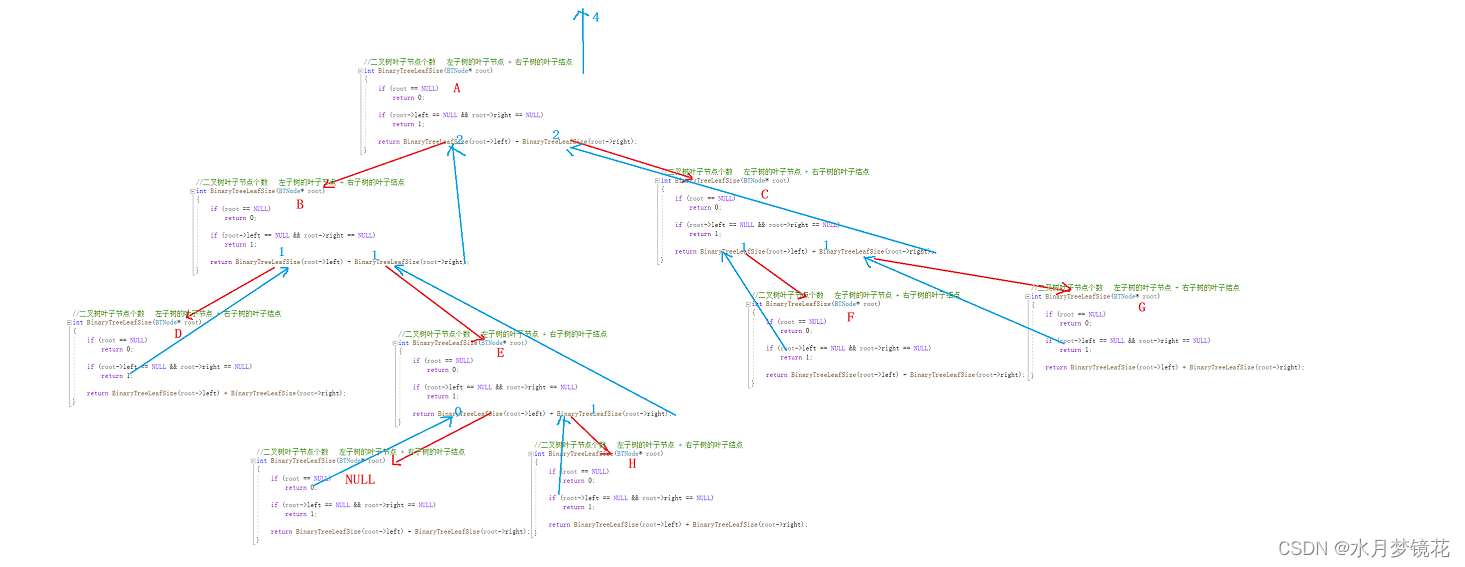
在这里插入图片描述
在这里插入图片描述

二叉树查找值为X的节点(BinaryTreeFind)

先序遍历查找节点，如果是该节点，直接返回该节点地址。如果不是该节点，继续查找该节点的左子树，如果左子树也没找到，查找右子树。

//二叉树查找值为X的节点   前序遍历查找  
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;//根if (root->data == x)return root;//左子树BTNode* leftNode = BinaryTreeFind(root->left, x);if (leftNode != NULL)return leftNode;//右子树BTNode* rightNode = BinaryTreeFind(root->right, x);if (rightNode != NULL)return rightNode;return NULL;
}

对于下面二叉树，查找 ’ C '的递归展开图
在这里插入图片描述
在这里插入图片描述

判断二叉树是否是完全二叉树(BinaryTreeComplete)

完全二叉树也就是堆，当其层序遍历时，其中有效数据(不包含NULL)是连续的。
只需要借助队列，来层序遍历二叉树(如果某个节点左子节点或右子节点是NULL也入队列)。当队列首数据是NULL时，判断其后数据是否全是NULL，如果其后数据全是NULL，返回true，如果其后元素有一个不是NULL，返回false。


//完全二叉树的节点是连续的，层序遍历二叉树，如果遇到NULL，检查栈中后续元素是否都为NULL
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);QuenePush(&q, root);while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QuenePush(&q, node->left);QuenePush(&q, node->right);}else{break;}}while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QueneDestrory(&q);return false;}}QueneDestrory(&q);return true;
}

通过前序遍历的数组构建二叉树

在先序遍历的数组中，我们以’ # '代表NULL。
函数声明：其中a是先序遍历的数组，n是节点数，pi是现在节点的个数

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);

子问题：构建左子树与右子树
结束条件：遇到先序遍历数组的’ # '或节点数大于n
创建根节点，再遍历左子树和右子树，使根节点指向左子树与右子树。

//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n  || a[*pi] == '#'){(*pi)++;return NULL;}BTNode* newnode = BuyBinaryTreeNode(a[*pi]);(*pi)++;//左子节点BTNode* leftnode = BinaryTreeCreate(a, n, pi);newnode->left = leftnode;//右子节点BTNode* rightnode = BinaryTreeCreate(a, n, pi);newnode->right = rightnode;return newnode;
}

四、代码展示

二叉树代码展示

#pragma once#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <string.h>typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);//二叉树的销毁
void BinaryTreeDestroy(BTNode* root);//二叉树节点个数
int BinaryTreeSize(BTNode* root);//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);//二叉树第K层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);//二叉树查找值为X的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);//二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);//二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);//二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);//层序遍历
void BinaryTreeLevelOrder(BTNode* root);//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x);

#include "BinaryTree.h"
#include "quene.h"//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x)
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc:");exit(-1);}root->data = x;root->left = root->right = NULL;return root;
}//二叉树前序遍历   根节点 左子树  右子树
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//根节点printf("%c ", root->data);//左子树BinaryTreePrevOrder(root->left);//右子树BinaryTreePrevOrder(root->right);
}//二叉树中序遍历		左子树  根  右子树
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreeInOrder(root->left);//根printf("%c ", root->data);//右子树BinaryTreeInOrder(root->right);
}//二叉树后序遍历  左子树 右子树 根
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreePostOrder(root->left);//右子树BinaryTreePostOrder(root->right);//根printf("%c ", root->data);
}//二叉树的销毁  后序遍历二叉树 
void BinaryTreeDestroy(BTNode* root)
{if (root == NULL){return;}//左子树BinaryTreeDestroy(root->left);//右子树BinaryTreeDestroy(root->right);//根free(root);
}//二叉树节点个数   根节点的左子树与右子树的节点个数和  
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}//        左子树节点数                 右子树节点数               根节点return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}//二叉树叶子节点个数   左子树的叶子节点 + 右子树的叶子结点
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}//二叉树第K层节点个数       左子树的第k层节点数 + 右子树的第k层节点数     不同栈帧的k互不影响
int BinaryTreeLevelKSize(BTNode* root, int k)
{//如果 k 超过数的深度if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}//二叉树查找值为X的节点   前序遍历查找  
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;//根if (root->data == x)return root;//左子树BTNode* leftNode = BinaryTreeFind(root->left, x);if (leftNode != NULL)return leftNode;//右子树BTNode* rightNode = BinaryTreeFind(root->right, x);if (rightNode != NULL)return rightNode;return NULL;
}//层序遍历  借助队列  出队头数据时，将其左子节点 与 右子节点依次入队列
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);//入根节点QuenePush(&q, root);//队列为空，代表二叉树中元素也遍历完成while (!QueneEmpty(&q)){QDataType val = QueneFront(&q);printf("%c ", val->data);//入数据  该节点的左节点 与 右节点if (val->left != NULL)QuenePush(&q, val->left);if (val->right != NULL)QuenePush(&q, val->right);//出队头数据QuenePop(&q);}QueneDestrory(&q);
}//判断二叉树是否是完全二叉树    层序遍历二叉树//bool BinaryTreeComplete(BTNode* root)
//{
//	Quene q;
//	QueneInit(&q);
//
//	//如果某个节点的右节点为空，那么之后遍历的节点的左/右节点也应该为空
//	bool flag = false;
//
//	QuenePush(&q, root);
//	while (!QueneEmpty(&q))
//	{
//		QDataType val = QueneFront(&q);
//
//		if (val->left == NULL && val->right != NULL)
//			return false;
//
//		if (flag == true && (val->left != NULL || val->right != NULL))
//			return false;
//
//		if (val->left != NULL)
//			QuenePush(&q, val->left);
//
//		if (val->right != NULL)
//			QuenePush(&q, val->right);
//		else
//			flag = true;
//
//		QuenePop(&q);
//	}
//
//	return true;
//}//完全二叉树的节点是连续的，层序遍历二叉树，如果遇到NULL，检查栈中后续元素是否都为NULL
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);QuenePush(&q, root);while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QuenePush(&q, node->left);QuenePush(&q, node->right);}else{break;}}while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QueneDestrory(&q);return false;}}QueneDestrory(&q);return true;
}//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n  || a[*pi] == '#'){(*pi)++;return NULL;}BTNode* newnode = BuyBinaryTreeNode(a[*pi]);(*pi)++;//左子节点BTNode* leftnode = BinaryTreeCreate(a, n, pi);newnode->left = leftnode;//右子节点BTNode* rightnode = BinaryTreeCreate(a, n, pi);newnode->right = rightnode;return newnode;
}

队列代码展示

#include "BinaryTree.h"
#include <assert.h>//队列 节点结构--树节点
typedef struct QueneNode
{struct BinaryTreeNode* data;struct QueneNode* next;
}QueneNode;typedef struct BinaryTreeNode* QDataType;//队列 结构
typedef struct Quene
{QueneNode* head;QueneNode* tail;int size;
}Quene;//初始化队列
void QueneInit(Quene* q);//队尾入队列
void QuenePush(Quene* q, QDataType x);//队头出数据
void QuenePop(Quene* q);//获取队列头部元素
QDataType QueneFront(Quene* q);//获取队列队尾元素
QDataType QueneBack(Quene* q);//获取队列中有效元素个数
int QueneSize(Quene* q);//检查队列是否为空，如果为空返回ture，如果非空返回false
bool QueneEmpty(Quene* q);//销毁队列
void QueneDestrory(Quene* q);

#include "quene.h"//初始化队列
void QueneInit(Quene* q)
{assert(q);q->head = q->tail = NULL;q->size = 0;
}//队尾入队列
void QuenePush(Quene* q, QDataType x)
{assert(q);QueneNode* newnode = (QueneNode*)malloc(sizeof(QueneNode));if (newnode == NULL){perror("malloc");exit(-1);}newnode->next = NULL;newnode->data = x;//队列为空if (QueneEmpty(q) == true){q->head = q->tail = newnode;}else//队列不为空{q->tail->next = newnode;q->tail = newnode;}q->size++;
}//队头出数据
void QuenePop(Quene* q)
{assert(q);//队列为空assert(QueneEmpty(q) != true);//队列只有一个元素if (q->head->next == NULL){free(q->head);q->head = q->tail = NULL;}else//队列中有多个元素{QueneNode* next = q->head->next;free(q->head);q->head = next;}q->size--;
}//获取队列头部元素
QDataType QueneFront(Quene* q)
{assert(q);return q->head->data;
}//获取队列队尾元素
QDataType QueneBack(Quene* q)
{assert(q);return q->tail->data;
}//获取队列中有效元素个数
int QueneSize(Quene* q)
{assert(q);return q->size;
}//检查队列是否为空，如果为空返回ture，如果非空返回false
bool QueneEmpty(Quene* q)
{assert(q);return q->size == 0;
}//销毁队列
void QueneDestrory(Quene* q)
{assert(q);QueneNode* cur = q->head;while (cur){QueneNode* next = cur->next;free(cur);cur = next;}}

总结

以上就是我对于二叉树的理解！！！
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/96634.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

一百五十六、Kettle——Linux上安装的Kettle9.3连接ClickHouse数据库（亲测，附流程截图）

一百五十六、Kettle——Linux上安装的Kettle9.3连接ClickHouse数据库（亲测，附流程截图）

一、目标 kettle9.3在Linux上安装好后&#xff0c;需要与ClickHouse数据库建立连接 二、前提准备 &#xff08;一&#xff09;在Linux已经安装好kettle并可以启动kettle &#xff08;二&#xff09;已知kettle和ClickHouse版本 1、kettle版本是9.3 2、ClickHouse版本是21…
阅读更多...
浏览器控制台调试实用方法

浏览器控制台调试实用方法

许多程序员仅知道控制台的console.log&#xff0c;其实控制台API还包含一些其他实用方法&#xff0c; 这些方法在前端调试时会很有帮助。 目录 console.dir 查看对象属性和方法 输出DOM元素 console.error console.time和console.timeEnd console.log console.clear 总结…
阅读更多...
Oracle切割字符串的方法，SQL语句完成。

Oracle切割字符串的方法，SQL语句完成。

Oracle用正则的方式循环切割字符串 需求&#xff1a;有一个这样子的 Str “‘CNJ-520-180500000001|CNJ-520-181200000001|CNJ-520-190300000001|CNJ-520-190100000001|CNJ-520-181200000002’” &#xff0c;然后我需要拿到每一个单号&#xff0c;每一个单号都要走一遍固定的…
阅读更多...
Flask-SQLAlchemy

Flask-SQLAlchemy

认识Flask-SQLAlchemy Flask-SQLAlchemy 是一个为 Flask 应用增加 SQLAlchemy 支持的扩展。它致力于简化在 Flask 中 SQLAlchemy 的使用。SQLAlchemy 是目前python中最强大的 ORM框架, 功能全面, 使用简单。 ORM优缺点 优点 有语法提示, 省去自己拼写SQL&#xff0c;保证SQL…
阅读更多...
35_windows环境debug Nginx 源码-CLion配置CMake和启动

35_windows环境debug Nginx 源码-CLion配置CMake和启动

文章目录 生成 CMakeLists.txt 组态档35_windows环境debug Nginx 源码-CLion配置CMake和启动生成 CMakeLists.txt 组态档 修改auto目录configure文件，在 . auto/make 上边增加 . auto/cmake, 大概在 106 行。在 auto 目录下创建cmake 文件其内容如下： #!/usr/bin/env bash NG…
阅读更多...
C++ string类详解

C++ string类详解

⭐️ string string 是表示字符串的字符串类&#xff0c;该类的接口与常规容器的接口基本一致&#xff0c;还有一些额外的操作 string 的常规操作&#xff0c;在使用 string 类时&#xff0c;需要使用 #include <string> 以及 using namespace std;。 ✨ 帮助文档&…
阅读更多...
React入门 jsx学习笔记

React入门 jsx学习笔记

一、JSX介绍 概念&#xff1a;JSX是 JavaScript XML&#xff08;HTML&#xff09;的缩写&#xff0c;表示在 JS 代码中书写 HTML 结构 作用&#xff1a;在React中创建HTML结构&#xff08;页面UI结构&#xff09; 优势&#xff1a; 采用类似于HTML的语法&#xff0c;降低学…
阅读更多...
图神经网络 day2 图的分类

图神经网络 day2 图的分类

图神经网络基础算法 1 GCN2 GraphSAGE2.1 采样&#xff1a;采样固定长度的邻居2.2 聚合2.3 GraphSAGE_minibatch2.4 GraphSAGE_embedding 3 GAT4. 图网络的分类4.1 递归图神经网络 RGNN4.2 图卷积神经网络GCN4.3 图注意力网络 GAT4.4 图自动编码 GAE4.5 图时空网络 GSTN4.6 图生…
阅读更多...
opencv-目标追踪

opencv-目标追踪

import argparse import time import cv2 import numpy as np# 配置参数 ap argparse.ArgumentParser() ap.add_argument("-v", "--video", typestr,help"path to input video file") ap.add_argument("-t", "--tracker", …
阅读更多...
linux系统服务学习（六）FTP服务学习

linux系统服务学习（六）FTP服务学习

文章目录 FTP、NFS、SAMBA系统服务一、FTP服务概述1、FTP服务介绍2、FTP服务的客户端工具3、FTP的两种运行模式&#xff08;了解&#xff09;☆ 主动模式☆ 被动模式 4、搭建FTP服务&#xff08;重要&#xff09;5、FTP的配置文件详解&#xff08;重要&#xff09; 二、FTP任务…
阅读更多...
Git 设置代理

Git 设置代理

Git 传输分两种协议&#xff0c;SSH和 http(s)&#xff0c;设置代理也需要分两种。 http(s) 代理 Command Line 使用 命令行 模式&#xff0c;可以在Powershell中使用以下命令设置代理&#xff1a; $env:http_proxy"http://127.0.0.1:7890" $env:https_proxy&quo…
阅读更多...
12-数据结构-数组、矩阵、广义表

12-数据结构-数组、矩阵、广义表

数组、矩阵、广义表 目录 数组、矩阵、广义表 一、数组 二.矩阵 三、广义表 一、数组 这一章节理解基本概念即可。数组要看清其实下标是多少&#xff0c;并且二维数组&#xff0c;存取数据&#xff0c;要先看清楚是按照行存还是按列存&#xff0c;按行则是正常一行一行的去读…
阅读更多...
【AIGC 讯飞星火 | 百度AI|ChatGPT| 】智能对比

【AIGC 讯飞星火 | 百度AI|ChatGPT| 】智能对比

AI智能对比 &#x1f378; 前言&#x1f37a; 概念类对比&#x1f375; 讯飞&#x1f375; 百度AI&#x1f375; chatGPT &#x1f379; 功能类对比☕ 讯飞☕ 百度AI☕ chatGPT &#x1f943; 可输入字数对比&#x1f964; 百度AI&#x1f964; 讯飞&#x1f964; chatGPT &…
阅读更多...
认识Transformer：入门知识

认识Transformer：入门知识

视频链接&#xff1a; https://www.youtube.com/watch?vugWDIIOHtPA&listPLJV_el3uVTsOK_ZK5L0Iv_EQoL1JefRL4&index60 文章目录 Self-Attention layerMulti-head self-attentionPositional encodingSeq2Seq with AttentionTransformerUniversal Transformer Seq2Seq …
阅读更多...
ansible入门

ansible入门

ansible入门 一.ansible 背景介绍 Ansible 是一个广受欢迎的 IT 自动化系统。可以用来处理配置管理、应用自动化部署、云资源配给、网络 自动化和多借点部署等任务。其也可以使得复杂的变更如带负载均衡的零停机滚动更新更加容易。Ansible.com 1.1 自动化运维概念 1.1.1 运维…
阅读更多...
专业课只考2门，计算机学硕最低分290的江苏院校

专业课只考2门，计算机学硕最低分290的江苏院校

南京工业大学 考研难度&#xff08;☆&#xff09; 内容&#xff1a;23考情概况&#xff08;拟录取和复试分析&#xff09;、专业目录、23复试详情、各专业考情分析。 正文1332字&#xff0c;预计阅读&#xff1a;3分钟。 2023考情概况 南京工业大学计算机相关各专业复试和…
阅读更多...
超实用的批量管理工具 pssh 和 window 文件传输工具 pscp

超实用的批量管理工具 pssh 和 window 文件传输工具 pscp

文章目录 一、概述1&#xff09;pssh2&#xff09;pscp 二、pssh 工具安装三、pssh 命令的基本语法四、pscp 工具安装1&#xff09;Windows 上安装2&#xff09;Linux 系统上安装 五、 pscp 命令的基本语法1&#xff09;从 windows 向 linux 传文件2&#xff09;从 linux 传文件…
阅读更多...
Golang协程,通道详解

Golang协程,通道详解

进程、线程以及并行、并发 关于进程和线程 进程&#xff08;Process&#xff09;就是程序在操作系统中的一次执行过程&#xff0c;是系统进行资源分配和调度的基本单位&#xff0c;进程是一个动态概念&#xff0c;是程序在执行过程中分配和管理资源的基本单位&#xff0c;每一…
阅读更多...
在APP中如何嵌入小游戏？

在APP中如何嵌入小游戏？

APP内嵌游戏之所以能火爆&#xff0c;主要是因为互联网对流量的追求是无止境的&#xff0c;之前高速增长的红利期后&#xff0c;获取新的流量成为各大厂商的挑战&#xff0c;小游戏的引入&#xff0c;就是这个目的&#xff0c;为已有的产品赋能&#xff0c;抢占用户注意力和使用…
阅读更多...
leetcode 139. 单词拆分

leetcode 139. 单词拆分

2023.8.18 本题可以看作完全背包问题&#xff0c;字符串s为背包&#xff0c;字符串列表worddict中的字符串为物品。由于本题的物品集合是排列问题(即物品的排列顺序对结果有影响)&#xff0c;所以遍历顺序为&#xff1a;先遍历背包再遍历物品。 接下来看代码&#xff1a; clas…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023