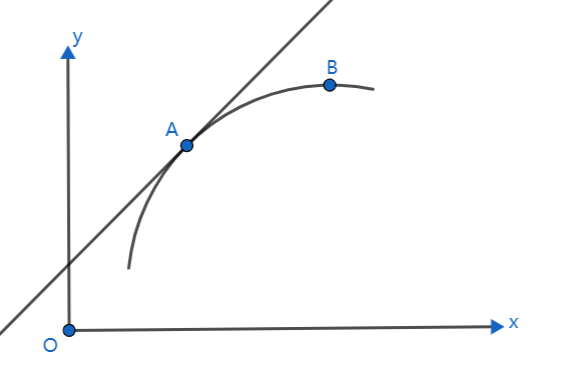
本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。
如上图所示。 设 y = f ( x ) , x = φ ( t ) , y = ψ ( t ) 当 t = t 0 时, x = x 0 , y = y 0 ,即点 A 坐标为 ( x 0 , y 0 ) 点 A 处的导数 f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) φ ( t 0 + Δ t ) − φ ( t 0 ) = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / lim Δ t → 0 φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = ψ ′ ( t 0 ) φ ′ ( t 0 ) 因此点 A 处的切线向量可表示为 ( ψ ′ ( t 0 ) , φ ′ ( t 0 ) ) 而切线方程为 y − y 0 = ψ ′ ( t 0 ) φ ′ ( t 0 ) ( x − x 0 ) ,即 y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) 同理可得空间直线的点向式方程为: y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) = z − z 0 ω ′ ( t 0 ) 如上图所示。\\ 设y=f(x),x=\varphi(t),y=\psi(t) \\ 当t=t_0时,x=x_0,y=y_0,即点A坐标为(x_0,y_0) \\ 点A处的导数f^\prime(x_0)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\varphi(t_0+\Delta t)-\varphi(t_0)} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\lim_{\Delta t \to 0}\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)} \\ \,\\ 因此点A处的切线向量可表示为(\psi^\prime(t_0),\varphi^\prime(t_0)) \\ 而切线方程为y-y_0=\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)}(x-x_0),即\frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)} \\ \,\\ 同理可得空间直线的点向式方程为:\\ \frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)}=\frac{z-z_0}{\omega^\prime(t_0)} 如上图所示。设y=f(x),x=φ(t),y=ψ(t)当t=t0时,x=x0,y=y0,即点A坐标为(x0,y0)点A处的导数f′(x0)=Δx→0limΔxΔy=Δt→0limφ(t0+Δt)−φ(t0)ψ(t0+Δt)−ψ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δtφ(t0+Δt)−φ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δt→0limΔtφ(t0+Δt)−φ(t0)=φ′(t0)ψ′(t0)因此点A处的切线向量可表示为(ψ′(t0),φ′(t0))而切线方程为y−y0=φ′(t0)ψ′(t0)(x−x0),即ψ′(t0)y−y0=φ′(t0)x−x0同理可得空间直线的点向式方程为:ψ′(t0)y−y0=φ′(t0)x−x0=ω′(t0)z−z0
专题:平面、空间直线参数方程下的切线斜率问题
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/111997.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
最简单vue获取当前地区天气--高德开放平台实现
目录 前言 一、注册成为高德平台开发者 二、注册天气key 1.点击首页右上角打开控制台 2.创建新应用 三、vue项目使用 1.打开vue项目找到public下的index.html,如果是vue3的话直接在主目录打开index.html文件就行,主要就是打开出口文件 编辑 2.根据高德…
元矿山下的音视频应用
// 近年来,矿业的技术和管理模式随着元宇宙的火爆和自动驾驶技术的发展逐渐变化、升级,进而衍生出元矿山的概念,音视频技术也在其中成为了关键一环。LiveVideoStackCon 2023 上海站邀请了来自希迪智驾的任思亮,为大家分享希迪智…
无限计算力:探索云计算的无限可能性
这里写目录标题 前言云计算介绍服务模型: 应用领域:云计算主要体现在生活中的地方云计算未来发展的方向 前言
云计算是一种基于互联网的计算模型,通过它可以实现资源的共享、存储、管理和处理。它已经成为许多个人、企业和组织的重要技术基础…
MySQL数据库学习【基础篇】
📃基础篇 下方链接使用科学上网速度可能会更加快一点哦! 请点击查看数据库MySQL笔记大全
通用语法及分类
DDL: 数据定义语言,用来定义数据库对象(数据库、表、字段)DML: 数据操作语言,用来对数据库表中的…
mybatis与spring集成与spring aop集成pagehelper插件
Mybatis与Spring的集成
Mybatis是一款轻量级的ORM框架,而Spring是一个全栈式的框架,二者的结合可以让我们更加高效地进行数据持久化操作。
Mybatis与Spring的集成主要有两种方式:使用Spring的Mybatis支持和使用Mybatis的Spring支持。
使用…
再获殊荣 | 美格智能高算力AI模组SNM970荣获物联网行业“通信技术创新奖”
8月28日,由高科技行业门户OFweek维科网主办的OFweek 2023(第八届)物联网产业大会暨评选颁奖典礼在深圳福田会展中心隆重举行。会上正式公布了OFweek 2023(第八届)物联网与人工智能行业年度评选奖项,美格智能…
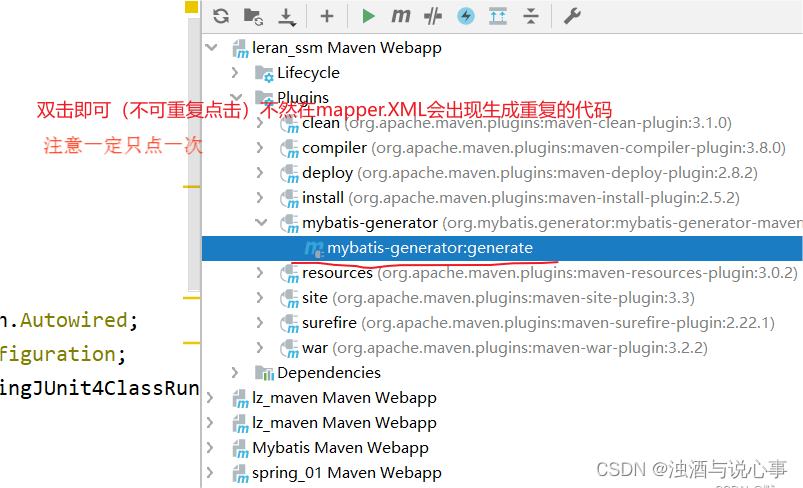
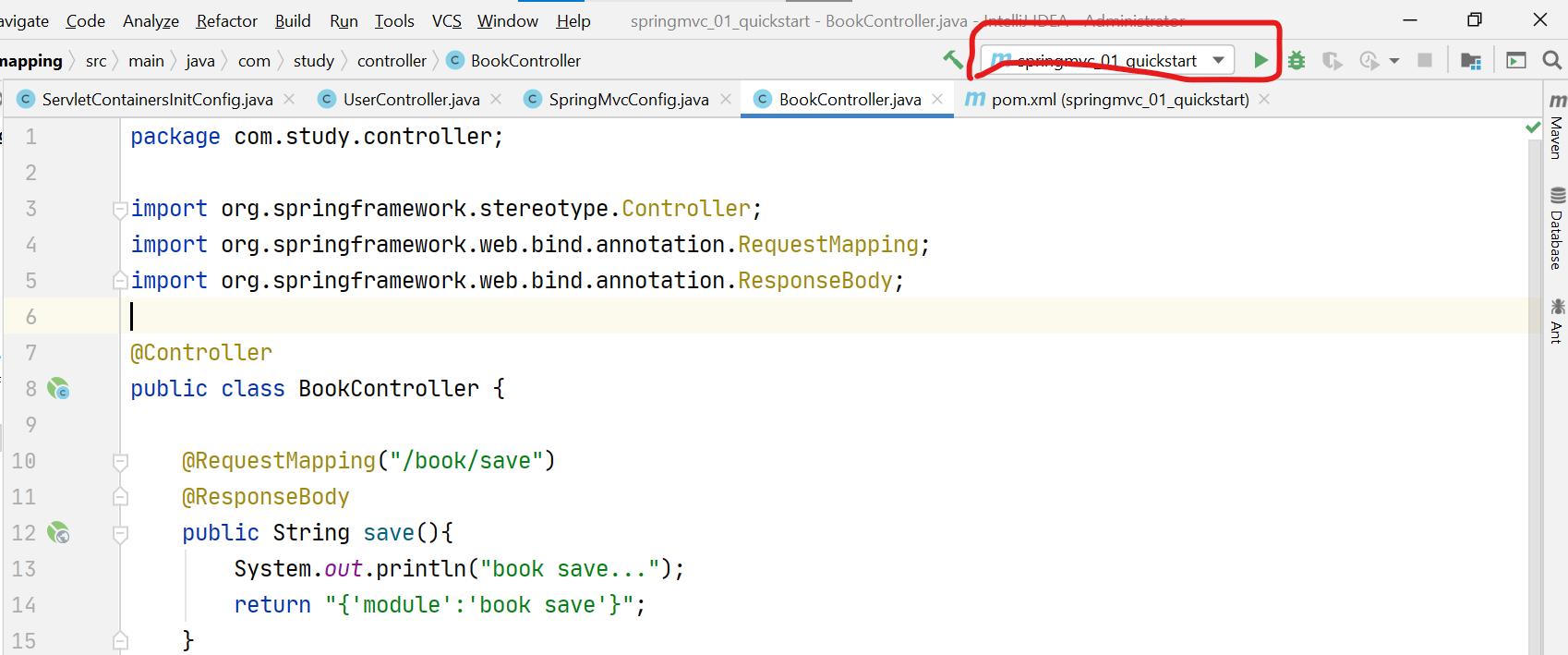
springmvc没有绿标,怎么配置tomcat插件运行?
一、添加插件后,刷新,自动从maven仓库下载tomcat插件 二、写好项目后,添加tomcat配置 三、即可点击绿标运行
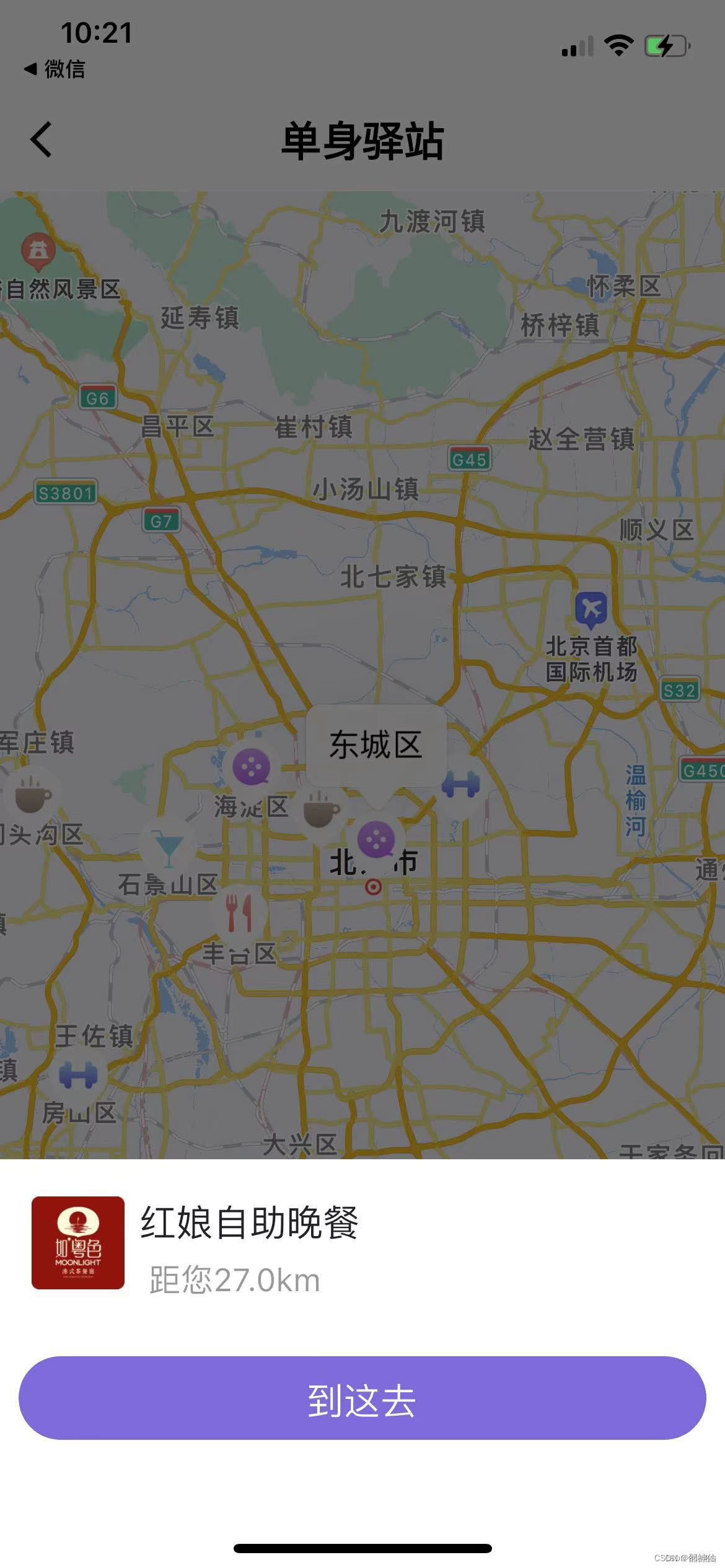
flutter高德地图大头针
1、效果图 2、pub get
#地图定位 amap_flutter_map: ^3.0.0 amap_flutter_location: ^3.0.0
3、上代码
import dart:async;
import dart:io;import package:amap_flutter_location/amap_flutter_location.dart;
import package:amap_flutter_location/amap_location_option…
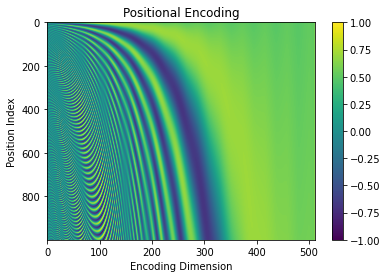
用变压器实现德-英语言翻译【02/8】: 位置编码
一、说明 本文是“用变压器实现德-英语言翻译”系列的第二篇。它从头开始引入位置编码。然后,它解释了 PyTorch 如何实现位置编码。接下来是变压器实现。 二、技术背景 位置编码用于为序列中的每个标记或单词提供相对位置。阅读句子时,每个单词都依赖于它…
fastadmin think-queue supervisor配置
起因是微信支付回调需要同时做发货处理,但是发货接口不能影响,需要队列进行异步处理1.
1.fastadmin 后台购买queue插件(基于think-queue消息队列)
2.代码 2.1 添加文件:application---->extra--->queue.php 内容:我这里用的数据库做…
leetcode 42. 接雨水
2023.8.29 本题可以用双指针做,求出每一列能盛的雨水,再相加即可。不过暴力法会超时,需要优化。
双指针(暴力):
class Solution {
public:int trap(vector<int>& height) {int ans 0;for(int …
(牛客周赛 9)C.小美的01串翻转
题目: 样例: 输入 10001 输出 8 思路: 这里是连续的找子串,权值的意思是 我们取反操作了多少次,
我们有假设长度是 5 ,字符串是 10001
那么相邻不一样的字符串有两种情况 01010 或者 10101…
高等职业学校物联网实训室建设方案
一、概述
1.1专业背景
物联网(Internet of Things)被称为继计算机、互联网之后世界信息产业第三次浪潮,它并非一个全新的技术领域,而是现代信息技术发展到一定阶段后出现的一种聚合性应用与技术提升,是随着传感网、通…
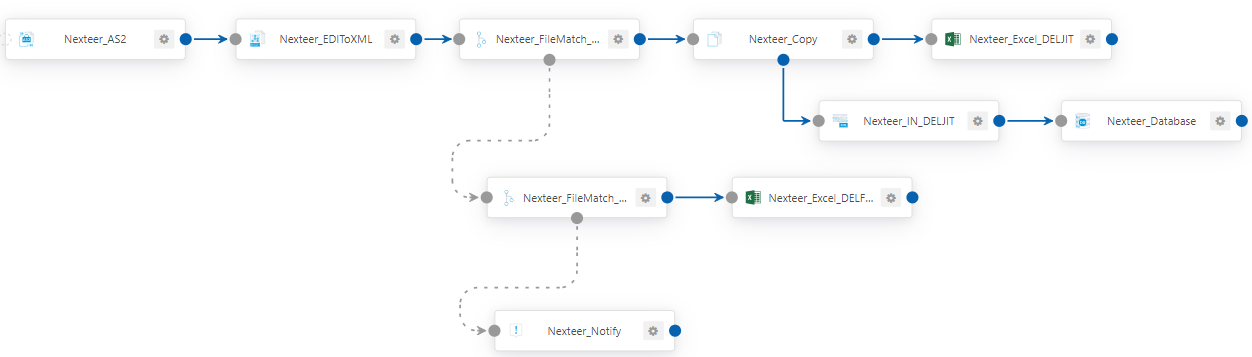
耐世特Nexteer EDI解决方案
耐世特Nexteer曾经为美国通用汽车全资子公司,是一家集研发、制造、销售于一体的全球化集团公司。耐世特汽车系统公司是转向系统及相关先进技术的全球供应商。该公司为60多家汽车制造商设计、制造、销售电动助力转向器、液压助力转向器、转向管柱和传动轴产品&#x…
GNU make系列之写Makefile文件(1)
一.欢迎来到我的酒馆 在本章节介绍如何写Makefile文件。 目录 一.欢迎来到我的酒馆二.Makefile包含了什么三.引入其它的Makefile文件四.MAKEFILES变量 二.Makefile包含了什么 2.1 Makefile包含了5种类型:显式的规则,隐式的规则,变量的定义&am…
数据结构:八种数据结构大全
数据结构 1.1 数据结构概述 数据结构是计算机存储、组织数据的方式;通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构的优良将直接影响着我们程序的性能;常用的数据结构有:数组(Arrayÿ…
【Qt学习】05:自定义封装界面类
OVERVIEW 自定义封装界面类1.QListWidget2.QTreeWidget3.QTableWidget4.StackedWidget5.Others6.自定义封装界面类-显示效果(1)添加设计师界面类(2)在ui中设计自定义界面(3)在需要使用的界面中添加…
【前端】常用功能合集
目录 js跳转到新标签打开PDF文件js每十个字符换行 es6用表达式或变量名作为对象的属性名 vuev-for插值、:style、:class父组件加载完后再加载子组件keep-alive缓存跨域请求第三方接口跨域请求之callback(不建议)读取本地文件浏览器播放提示音audio jquer…
最新文章
- wordpress不支持ie9/媒体平台
- 帮人家做网站难吗/杭州百度推广
- 做微信网站支付需要什么信息表/seo营销策略
- 邢台做网站的/网页设计模板html代码
- 山东爱易网站建设工作室/win10优化
- 网页转图片/seo顾问服务福建
- 计算机毕业设计PyFlink+Hadoop广告推荐系统 广告预测 广告数据分析可视化 广告爬虫 大数据毕业设计 Spark Hive 深度学习 机器学
- WPF自定义窗口 输入验证不生效
- java后端传时间戳给前端的三种方式
- (2024.12)Ubuntu20.04安装openMVS<成功>.colmap<成功>和openMVG<失败>记录
- LeetCode429周赛T4
- HTTP、HTTPS和SOCKS5代理協議
推荐文章
- 黄仁勋对台积电放核弹 干掉4万台CPU服务器计算光刻加速40倍
- # Lua与C++交互(二)———— 交互
- #RAG|NLP|Jieba|PDF2WORD# pdf转word-换行问题
- (13)DroneCAN 适配器节点(二)
- (2)(2.14) SPL Satellite Telemetry
- (6)(6.6) 恢复任务回放
- (7) cmake 编译C++程序(二)
- (CVPR-2022)感知优先的扩散模型训练
- (done) Beam search
- (done) Go 语言:三种多文件协作方式
- (mac)Promethues监控之mysqld_exporter(MySQL监控)
- (Spring学习06)Spring之循环依赖底层源码解析