1--用栈实现队列

利用两个栈，一个是输入栈，另一个是输出栈；

#include <iostream>
#include <stack>class MyQueue {
public:MyQueue() {}void push(int x) {in_stk.push(x);}int pop() {if(out_stk.empty()){while(!in_stk.empty()){out_stk.push(in_stk.top());in_stk.pop();}}int tmp = out_stk.top();out_stk.pop();return tmp;}int peek() {if(out_stk.empty()){while(!in_stk.empty()){out_stk.push(in_stk.top());in_stk.pop();}}return out_stk.top();}bool empty() {if(out_stk.empty() && in_stk.empty()) return true;else return false;}
private:std::stack<int> in_stk, out_stk;
};int main(int argc, char* argv[]){MyQueue Queue;Queue.push(1);Queue.push(2);Queue.push(3);std::cout << Queue.pop() << std::endl;std::cout << Queue.peek() << std::endl;return 0;
}

2--用队列实现栈

主要思路：

弹出栈顶元素时，需要将队列前 size - 1 个元素先弹出再重新加入到队列中；

#include <iostream>
#include <queue>class MyStack {
public:MyStack() {}void push(int x) {q.push(x);}int pop() {int size = q.size();for(int i = 1; i <= size - 1; i++){q.push(q.front());q.pop();}int tmp = q.front();q.pop();return tmp;}int top() {int size = q.size();for(int i = 1; i <= size - 1; i++){q.push(q.front());q.pop();}int tmp = q.front();q.pop();q.push(tmp);return tmp;}bool empty() {return q.empty();}
private:std::queue<int> q;
};int main(int argc, char* argv[]){MyStack stk;stk.push(1);stk.push(2);stk.push(3);std::cout << stk.pop() << std::endl;std::cout << stk.top() << std::endl;return 0;
}

3--有效的括号

主要思路：

基于栈，遇到左括号，入栈对应的右括号。遇到右括号，判断当前栈顶元素是否与右括号相等，相等则表示之前曾遇到对应的左括号，表明匹配成功并弹出栈顶元素，否则返回 false；

最后判断栈是否为空，即是否有未匹配的左括号；

#include <iostream>
#include <stack>
#include <string>class Solution {
public:bool isValid(std::string s) {std::stack<char> stk;for(int i = 0; i < s.length(); i++){if(s[i] == '(') stk.push(')');else if(s[i] == '[') stk.push(']');else if(s[i] == '{') stk.push('}');else{if(stk.empty()) return false;else if(stk.top() != s[i]) return false;else stk.pop(); // 匹配}}return stk.empty();}
};int main(int argc, char* argv[]){std::string test = "()[]{}";Solution S1;bool res = S1.isValid(test);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}

4--删除字符串中的所有相邻重复项

主要思路：

基于栈，遍历字符串，判断当前字符与栈顶元素是否相同，相同则弹出栈顶元素，否则入栈；

最后遍历栈，将栈内的元素重构为字符串，需注意顺序；

#include <iostream>
#include <stack>
#include <string>class Solution {
public:std::string removeDuplicates(std::string s) {std::stack<char> stk;for(int i = 0; i < s.length(); i++){if(stk.empty() || stk.top() != s[i]){stk.push(s[i]);}else{ // s[i] == stk.top()stk.pop();}}std::string res;while(!stk.empty()){res = stk.top() + res;stk.pop();}return res;}
};int main(int argc, char* argv[]){std::string test = "abbaca";Solution S1;std::string res = S1.removeDuplicates(test);std::cout << res << std::endl;return 0;
}

5--逆波兰表达式求值

主要思路：

基于栈，遍历字符串数组，当遇到数字时将数字压入栈中，当遇到运算符时，将栈顶的两个元素取出来进行运算，并将运算结果重新压入栈中；

需注意运算顺序，即第二个出栈的 num2 作为运算符的左侧元素；

#include <iostream>
#include <vector>
#include <stack>
#include <string>class Solution {
public:int evalRPN(std::vector<std::string>& tokens) {std::stack<int> stk;for(int i = 0; i < tokens.size(); i++){if(tokens[i] != "+" && tokens[i] != "-" && tokens[i] != "*" && tokens[i] != "/"){stk.push(std::stoi(tokens[i]));continue;}int num1 = stk.top();stk.pop();int num2 = stk.top();stk.pop();if(tokens[i] == "+"){  int num3 = num2 + num1;stk.push(num3);continue;}else if(tokens[i] == "-"){int num3 = num2 - num1;stk.push(num3);continue;}else if(tokens[i] == "*"){int num3 = num2 * num1;stk.push(num3);continue;                }else{int num3 = num2 / num1;stk.push(num3);continue;}}return stk.top();}
};int main(int argc, char* argv[]){// tokens = ["2","1","+","3","*"]std::vector<std::string> test = {"2", "1", "+", "3", "*"};Solution S1;int res = S1.evalRPN(test);std::cout << res << std::endl;return 0;
}

6--滑动窗口的最大值

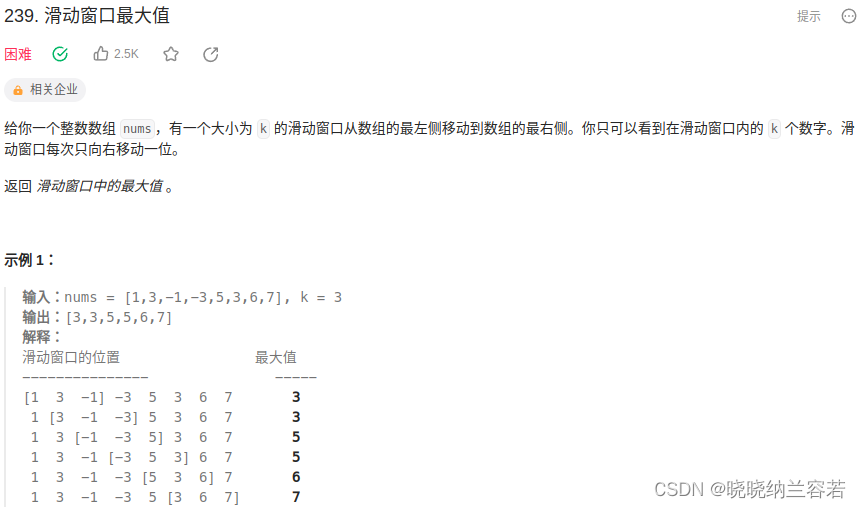
主要思路：

维护一个双端队列，队列里的元素存储的是可能成为最大值的元素，对于当前滑动窗口，其最大值为队头元素；

当移动滑动窗口时，需要判断当前移出窗口的元素是否是队头元素，如果是则需先将队头元素弹出（因为该元素已经离开了滑动窗口，相当于失效）；

之前本题的解法是存储元素的索引（之前的解法），这样可以避免重复元素的出现；但现在本题的解法是存储元素，所以一个细节是需要避免错误移除重复元素的问题，具体可以推导例子：[-7,-8,7,5,7,1,6,0]；

#include <iostream>
#include <vector>
#include <queue>class Solution {
public:std::vector<int> maxSlidingWindow(std::vector<int>& nums, int k) {std::deque<int> q; // 存储可能成为最大值的元素std::vector<int> res;// 初始化第一个滑动窗口for(int i = 0; i < k; i++){// 不能取等于号的原因是可能会出现相等的数，例如下例// [-7,-8,7,5,7,1,6,0] 出现了两个7，取=号会误弹出第2个7while(!q.empty() && q.back() < nums[i]){q.pop_back();}q.push_back(nums[i]);}res.push_back(q.front());// 遍历更新for(int i = k; i < nums.size(); i++){// 移除滑动窗口左边界的元素if(nums[i-k] == q.front()) q.pop_front();// 把不可能成为最大值的元素从队列中移出while(!q.empty() && q.back() < nums[i]){q.pop_back();}q.push_back(nums[i]);res.push_back(q.front()); // 记录当前滑动窗口的最大值}return res;}
};int main(int argc, char* argv[]){std::vector<int> test = {1, 3, -1, -3, 5, 3, 6, 7};int k = 3;Solution S1;std::vector<int> res = S1.maxSlidingWindow(test, k);for(auto v : res) std::cout << v << " ";std::cout << std::endl;return 0;
}

7--前k个高频元素

主要思路：

维护一个优先队列（小顶堆），里面存储 k 个元素及其出现的次数；

#include <iostream>
#include <vector>
#include <map>
#include <queue>class Solution {
public:std::vector<int> topKFrequent(std::vector<int>& nums, int k) {std::map<int, int> m;for(int i = 0; i < nums.size(); i++){m[nums[i]] += 1;}// 小顶堆std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, mycompare> pri_q;for(auto it = m.begin(); it != m.end(); it++){pri_q.emplace(*it);if(pri_q.size() > k) pri_q.pop(); // 始终维护 k 个 pair 对}// 倒叙输出k个高频元素std::vector<int> res(pri_q.size(), 0);for(int i = pri_q.size() - 1; i>=0; i--){res[i] = pri_q.top().first;pri_q.pop();}return res;}class mycompare{public:bool operator()(std::pair<int, int>& item1, std::pair<int, int>& item2){return item1.second > item2.second;}};
};int main(int argc, char* argv[]){// nums = [1,1,1,2,2,3], k = 2std::vector<int> test = {1, 1, 1, 2, 2, 3};int k = 2;Solution S1;std::vector<int> res = S1.topKFrequent(test, k);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/116987.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！