一、说明
模型预测路径积分控制(MPPI)是一种基于采样的模型预测控制算法。是MPC控制模型的延申和拓宽,要了解MPPI需要先理解MPC,参见文章:MPC预测控制概述和C++ 中的模型库-CSDN博客
二、模型预测路径积分 (MPPI) 控制
模型预测路径积分控制(MPPI)是一种基于采样的模型预测控制算法。MPPI 的第一个版本在 2016 年的 ICRA 上发布[pdf]。这项工作包括利用自由能和相对熵之间的信息论对偶性推导 MPPI,而实验包括使用 GT-AutoRally 车辆进行越野导航的应用。 MPPI 的后续版本包括 ICRA 2017 [pdf]和 TRO 2018 [pdf]中发布的非仿射动力学 MPPI 工作。自从第一次放弃出版物以来,ACDS 实验室以及其他实验室开发了不同的 MPPI 变体和形式。这些变体包括 Tube-MPPI、Robust-MPPI 和最新版本,例如 Tsallis-MPPI、约束协方差引导 – MPPI (CCS-MPPI) 和协方差控制-MPPI (CC-MPPI)。
基于采样类型的 MPC 算法可以使用不同的方法推导,包括自由能和相对熵之间的信息论对偶性、随机搜索方法和变分优化方法。每种方法都有其自身的优势,其中包括不同的算法特征、与标准 Hamilton-Jacobi-Belman 理论的联系、处理一般分布类别、随机过程和成本函数的灵活性,以及计算资源方面的要求。
Tube-MPPI:在基于 Tube 的 MPPI 中,有两个优化层,该架构的灵感来自于标准的基于 Tube 的模型预测和后退地平线控制架构。第一个优化层对应于普通 MPPI 算法,该算法使用标称对象或动力学的标称表示。第二层由微分动态规划控制器组成,跟踪由更高级别优化生成的轨迹。关于 Tube-MPPI 的论文首次发表在 RSS 2018 中,可以在链接中找到
Robust-MPPI:鲁棒模型预测路径积分控制旨在通过增强动态表示并将低级控制器洞察力与 MPPI 的随机优化模块相结合来克服 Tube-MPPI 的局限性。这使得RMPPI能够在地面导航任务中不那么保守并实现更高的速度。RMPPI 的其他功能包括选择下一个标称状态的优化步骤以及 RMPPI 的两个查询之间的性能界限。该界限是根据 RMPPI 的两个查询之间的自由能差计算的。关于RMPPI的论文出现在RAL 2021中,可以在链接中找到
Tsallis-MPPI:这是 MPPI 的扩展,依赖于变分优化和非扩展信息理论测量的使用。非广延信息论度量包括 Tsallis 熵和相应的散度。这些度量是香农熵和 Kulback Leibler 散度的概括。虽然 Tsallis 熵的有效性一直存在争议,但至少在工程应用中,它为可扩展且高效的随机优化算法的开发提供了有用的概括。在 Tsallis-MPPI 的背景下,我们的工作表明存在从交叉熵到 MPPI 的随机优化算法的连续体,它们是 Tsallis MPPI 的子情况。所提出的算法在性能以及不同任务和策略参数化(包括多模态和变分斯坦策略参数化)之间的一致性方面具有优势。Tsallis MPPI 的论文发表在 RSS 2021 中,可以在链接中找到
CCS-MPPI:约束协方差转向 MPPI 是一种基于管的 MPC 架构,它结合了基于采样的算法,例如 MPPI 和协方差转向控制算法。该架构由两层组成。第一层由生成最优状态分布的 MPPI 控制器组成。然后通过低级协方差控制算法跟踪状态分布。该算法是为线性系统开发的,与普通 MPPI 相比,在避障任务上的性能有所提高。CCS-MPPI 的工作首次发表在 ACC 2022 上,可以在链接中找到
CC-MPPI:协方差控制 MPPI 是一种将 MPPI 与协方差引导混合在一个层中的架构。这里的想法是,对于 MPPI 中生成的每个采样轨迹,都存在一个协方差转向问题,该问题提供一个具有相应采样轨迹平均值的椭球体。协方差引导算法提供控制,以围绕 MPPI 生成的每个采样轨迹引导协方差。这项工作的动机与提高 MPPI 的探索能力有关。论文首次发表于ICRA 2022,可在链接中找到
三、 模型预测控制(MPC)背景
MPC(考虑我之前的文章)是一种控制策略,它通过在每个时间步解决优化问题来计算控制动作。优化问题涉及预测系统在有限范围内的未来行为并找到最小化特定成本函数的控制序列。
记住。在 MPC 中,在每个时间步,我们在有限的预测范围内解决优化问题,以获得一系列控制输入。然而,只有该序列的第一个控制输入被应用到系统。然后,在下一个时间步,再次求解优化(考虑系统的新状态),并且再次仅应用第一个控制输入。这种“后退地平线”方法是 MPC 的基本特征。
四、模型预测路径积分(MPPI)控制器:
MPPI 是 MPC 的一个变体,它使用随机优化来计算控制动作。在 MPPI,我们考虑的不是解决确定性优化问题
,而是影响控制器性能的两个主要特征。
- 轨迹是指在给定一系列控制输入的情况下,系统随时间经过的状态序列。在 MPPI 的背景下,对多个轨迹进行采样以探索系统未来可能的不同行为。在 MPPI 中,对多个此类轨迹进行采样以探索状态和控制空间。这个想法是评估与每个轨迹相关的成本,然后使用该信息来确定最佳控制动作。
- 范围,通常称为预测或规划范围,是在优化问题中考虑未来轨迹的时间步数。它定义了控制器在做出决策时着眼于多远的未来。
MPPI 中的优化问题旨在找到在此范围内最小化预期成本的控制操作序列。
地平线 T 的选择至关重要:
如果地平线太短,控制器可能没有足够的远见来做出正确的决策,特别是在行动产生长期后果的情况下。
如果范围太长,计算复杂度可能会变得昂贵,特别是因为 MPPI 涉及对多个轨迹进行采样。此外,由于系统动力学或干扰的不确定性,对遥远未来的预测可能不太准确。

MPPI 概述(按作者)
MPPI 对多个控制轨迹进行采样并计算每个轨迹的预期成本。然后根据这些轨迹的加权平均值选择控制动作。
MPPI 背后的主要思想是使用随机最优控制的路径积分公式,它将轨迹的预期成本与其概率联系起来。
从数学上讲,MPPI 控制动作由下式给出:
目标函数:给定一个具有状态x和控制u的系统,目标是在有限范围T内最小化预期成本:

其中c ( xt , ut ) 是时间t的瞬时成本。
随机动力学:系统动力学由下式给出:
![]()
其中wt 是协方差为 Σ 的零均值高斯噪声。
采样:在每个时间步,K个控制轨迹,
![]()
从高斯分布中采样。
成本评估:使用系统动力学和成本函数计算每个采样轨迹的成本:

成本函数c ( xt , ut ) 可以根据所需的行为进行选择。例如,人们可以选择二次成本函数来惩罚与直立位置和大控制输入的偏差:

其中Q和R是正定矩阵。
加权组合:最优控制输入计算为采样控制轨迹的加权平均值:

其中权重ωk由下式给出:

这里,λ是决定加权锐度的温度参数。
五、车杆系统:
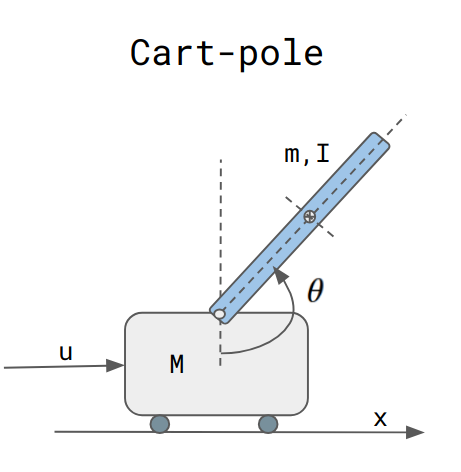
车杆(作者)
对于车杆系统,状态 x 定义为:
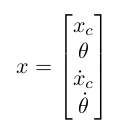
控制输入 u是施加到小车上的力。
车杆系统的动力学可以使用牛顿定律导出,并由下式给出:

这是 MPPI 控制器的简单模拟,您可以更改初始值,
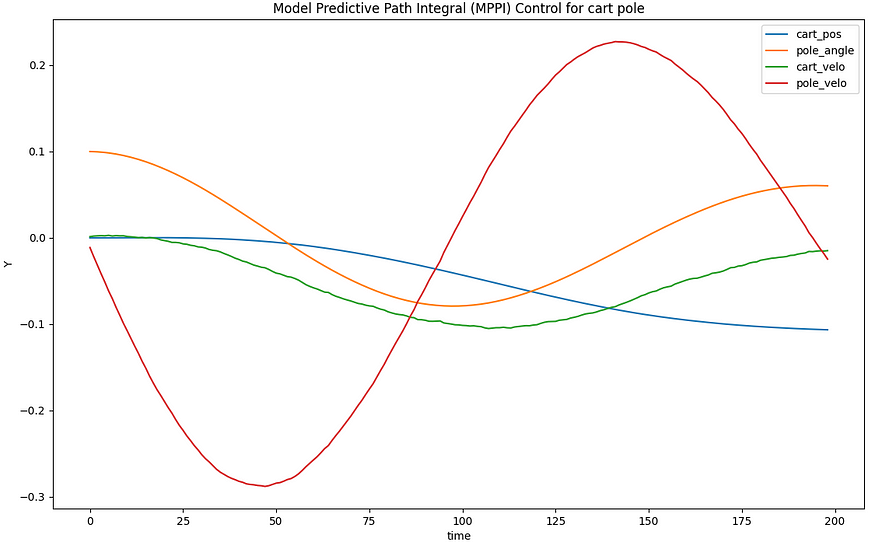
模拟结果(作者)
六、后记
本文是关于模型预测控制器 (MPC) 的讨论的延续。关于MPC资源请看:
你可以在GitHub上找到源代码。MPC预测控制概述和C++ 中的模型库