647. 回文子串

思路

动态规划

动规五部曲：

• 确定dp数组（dp table）以及下标的含义

如果大家做了很多这种子序列相关的题目，在定义dp数组的时候 很自然就会想题目求什么，我们就如何定义dp数组。

绝大多数题目确实是这样，不过本题如果我们定义，dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话，我们会发现很难找到递归关系。

dp[i] 和 dp[i-1] ，dp[i + 1] 看上去都没啥关系。

所以我们要看回文串的性质。 如图：

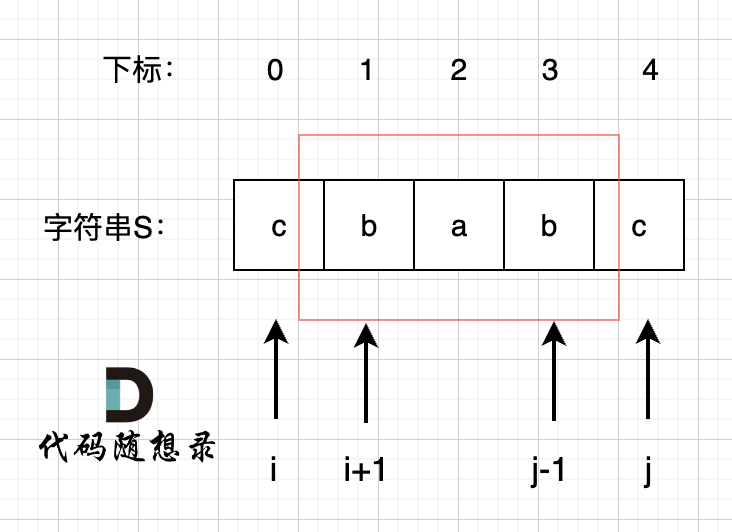
我们在判断字符串S是否是回文，那么如果我们知道 s[1]，s[2]，s[3] 这个子串是回文的，那么只需要比较 s[0]和s[4]这两个元素是否相同，如果相同的话，这个字符串s 就是回文串。

那么此时我们是不是能找到一种递归关系，也就是判断一个子字符串（字符串的下表范围[i,j]）是否回文，依赖于，子字符串（下表范围[i + 1, j - 1]）） 是否是回文。

所以为了明确这种递归关系，我们的dp数组是要定义成一位二维dp数组。

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

• 确定递推公式

在确定递推公式时，就要分析如下几种情况。

整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。

当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

• 情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
• 情况二：下标i 与 j相差为1，例如aa，也是回文子串
• 情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

以上三种情况分析完了，那么递归公式如下：

if (s[i] == s[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;}
}

result就是统计回文子串的数量。

注意这里我没有列出当s[i]与s[j]不相等的时候，因为在下面dp[i][j]初始化的时候，就初始为false。

• dp数组如何初始化

dp[i][j]可以初始化为true么？ 当然不行，怎能刚开始就全都匹配上了。

所以dp[i][j]初始化为false。

• 确定遍历顺序

遍历顺序可有有点讲究了。

首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。

dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：

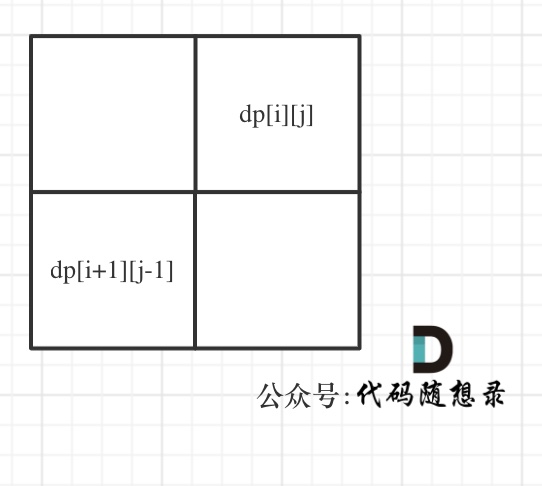
如果这矩阵是从上到下，从左到右遍历，那么会用到没有计算过的dp[i + 1][j - 1]，也就是根据不确定是不是回文的区间[i+1,j-1]，来判断了[i,j]是不是回文，那结果一定是不对的。

所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

有的代码实现是优先遍历列，然后遍历行，其实也是一个道理，都是为了保证dp[i + 1][j - 1]都是经过计算的。

代码如下：

for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍历顺序for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;}}}
}

• 举例推导dp数组

举例，输入："aaa"，dp[i][j]状态如下：

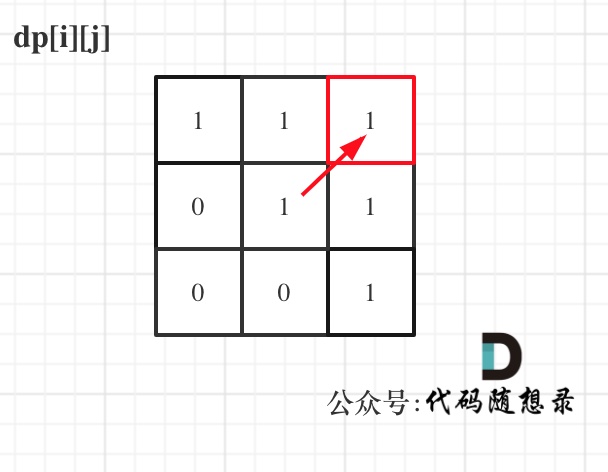
图中有6个true，所以就是有6个回文子串。

注意因为dp[i][j]的定义，所以j一定是大于等于i的，那么在填充dp[i][j]的时候一定是只填充右上半部分。

以上分析完毕，代码如下：

class Solution {public int countSubstrings(String s) {//[i][j] 表示从 i 到 j 是否为回文子串boolean[][] dp = new boolean[s.length()][s.length()];int result = 0;for (int i = s.length()-1; i >= 0; i--) {for (int j = i; j < s.length(); j++) {if (s.charAt(i) == s.charAt(j)){if (j-i <=1){ // 情况一 和 情况二dp[i][j] = true;result++;}else if (j-i>1){if (dp[i+1][j-1] == true){//情况三dp[i][j] = true;result++;}}}}}return result;}
}

---

516.最长回文子序列

思路

我们刚刚做过了 动态规划：回文子串 (opens new window)，求的是回文子串，而本题要求的是回文子序列， 要搞清楚这两者之间的区别。

回文子串是要连续的，回文子序列可不是连续的！ 回文子串，回文子序列都是动态规划经典题目。

回文子串，可以做这两题：

• 647.回文子串
• 5.最长回文子串

思路其实是差不多的，但本题要比求回文子串简单一点，因为情况少了一点。

动规五部曲分析如下：

• 确定dp数组（dp table）以及下标的含义

dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

• 确定递推公式

在判断回文子串的题目中，关键逻辑就是看s[i]与s[j]是否相同。

如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

如图： 

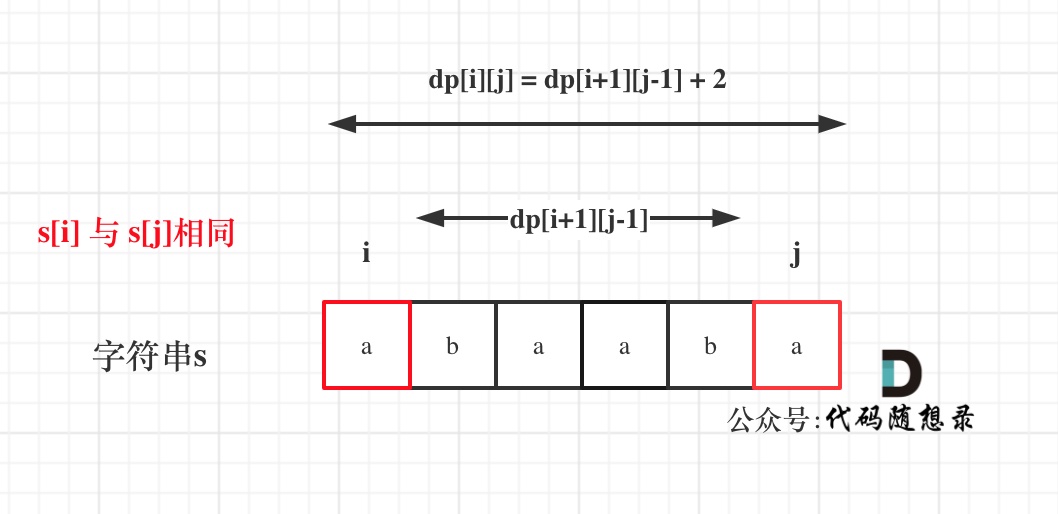
（如果这里看不懂，回忆一下dp[i][j]的定义）

如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为dp[i + 1][j]。

加入s[i]的回文子序列长度为dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

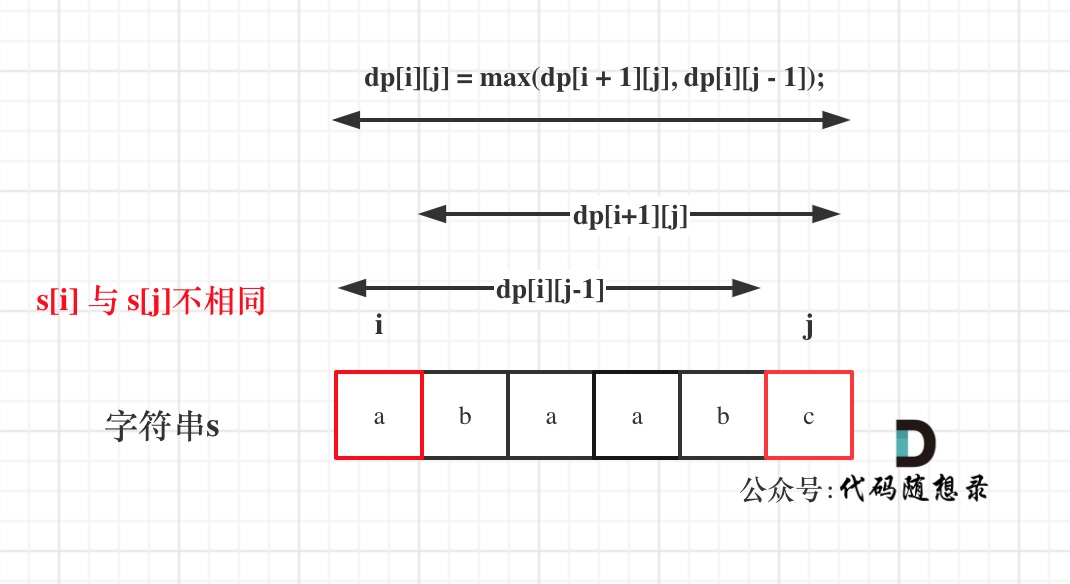
代码如下：

if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;
} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}

• dp数组如何初始化

首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。

所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。

其他情况dp[i][j]初始为0就行，这样递推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。

int[][] dp = new int[len][len];
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;

• 确定遍历顺序

从递归公式中，可以看出，dp[i][j] 依赖于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]，如图：

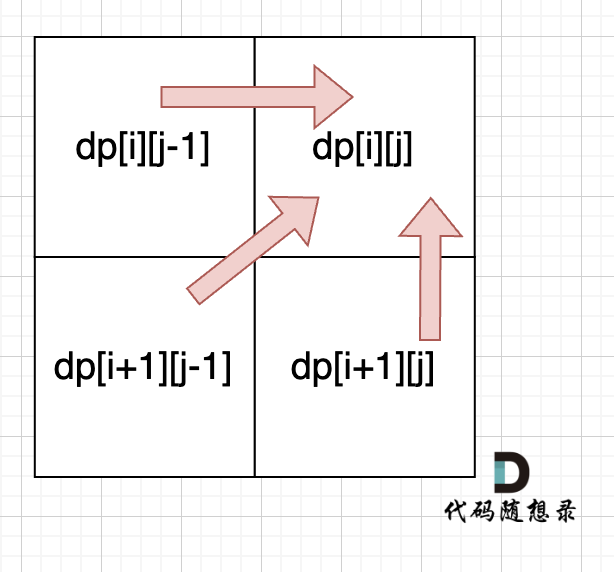
所以遍历i的时候一定要从下到上遍历，这样才能保证下一行的数据是经过计算的。

j的话，可以正常从左向右遍历。

代码如下：

for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}
}

• 举例推导dp数组

输入s:"cbbd" 为例，dp数组状态如图：

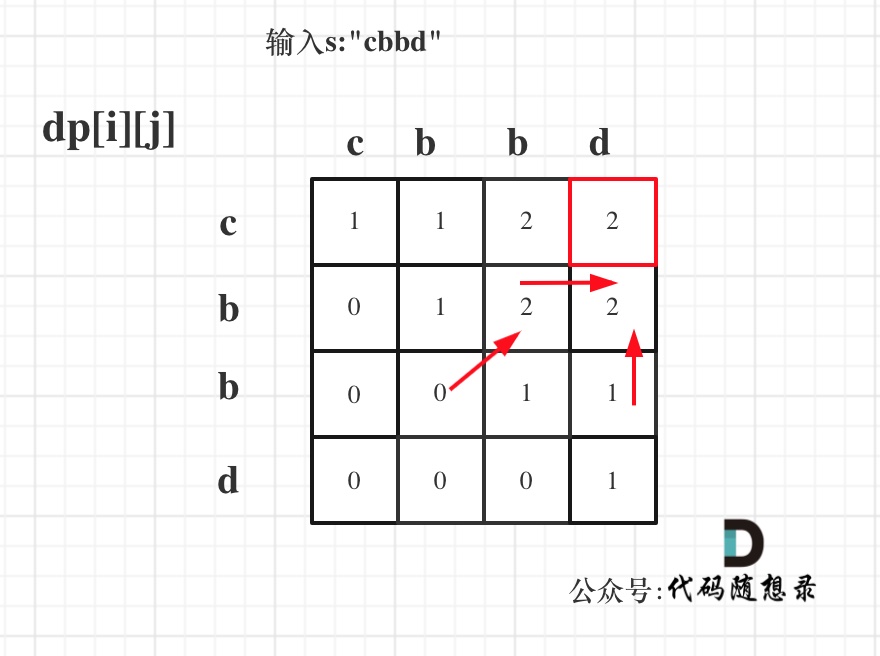
红色框即：dp[0][s.size() - 1]; 为最终结果。

以上分析完毕，代码如下：

class Solution {public int longestPalindromeSubseq(String s) {int len = s.length();int[][] dp = new int[len][len];for (int i = len - 1; i >= 0; i--) {dp[i][i] = 1;for (int j = i +1; j < len; j++) {if (s.charAt(i) == s.charAt(j)) {dp[i][j] = dp[i + 1][j - 1] + 2;}else {dp[i][j] = Math.max(dp[i+1][j-1],Math.max(dp[i+1][j],dp[i][j-1]));}}}return dp[0][len-1];}
}

• 时间复杂度: O(n^2)
• 空间复杂度: O(n^2)

---